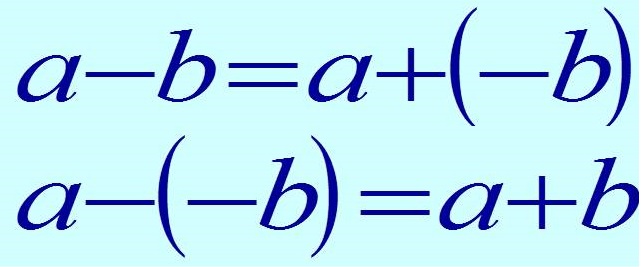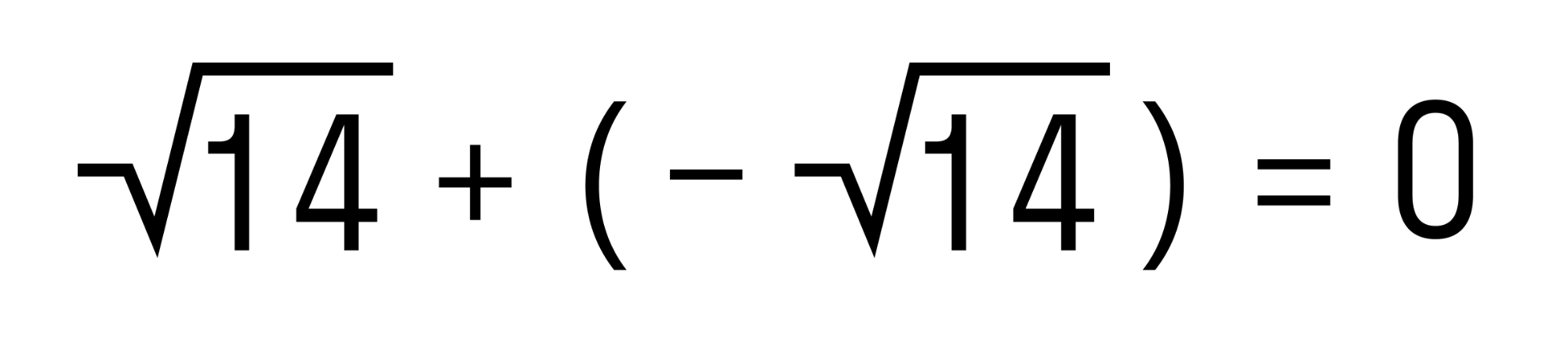Минусы и плюсы как считать
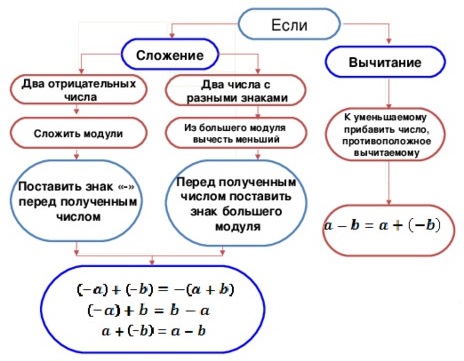
Правило сложения отрицательных чисел и чисел с разными знаками
Для суммирования двух отрицательных чисел, необходимо:
суммировать их модули;
перед полученной суммой поставить знак «минус».
В данном случае, складываем модули 9 и 6, и перед получившимся натуральным числом 15 ставим знак «-«.
Сложение рациональных или дробных чисел выполняется аналогичным способом:
К 26,35 прибавляем 25,35 (т. е. мы складываем модули), в итоге получаем 51,75 с отрицательным значением. Перед ним ставим знак «минус».
Для суммирования натуральных чисел со знаками «+» и «-», надо:
из слагаемого с большим значением модуля вычесть слагаемое с меньшим значением;
перед полученным результатом поставить знак того слагаемого, которое имело большее значение.
61,2 + (-31,5) = + (61,2 — 31,5) = 30,5
Модуль большего числа со знаком «+», соответственно, сумма получилась положительная:
Большее число со знаком «-», поэтому заменяем плюс на минус и получаем отрицательный ответ.
Как вычитать отрицательные и положительные числа
Для нахождения разности противоположных чисел, надо к уменьшаемому прибавить вычитаемое с противоположным знаком, то есть заменить разность суммой.
Наглядно данное действие лучше представить в виде формулы:
То есть любое выражение, содержащее знаки сложения и вычитания, следует решать как сумму чисел.
-6,1 + 5,6 = 5,6 + (-6,3) = 0,5.
Разность выражения будет положительной, если уменьшаемое больше вычитаемого, и отрицательной, если значение модуля уменьшаемого меньше вычитаемого. В случае, когда уменьшаемое и вычитаемое одинаковые, их разность будет равна нулю.
Если нужно отнять отрицательное число, то два знака «минус» подряд дают знак «плюс».
Все вышеперечисленные действия возможно выполнить на калькуляторе. Для этого достаточно ввести сначала модуль числа, потом нажать кнопку изменения знака «+/-».
Заключение
Для закрепления изученных правил можно использовать различные методы проверки знаний. На первом этапе лучшим вариантом будет тренажер, с помощью которого решение подобных примеров можно довести до автоматизма.
Так же для закрепления материала подойдет тестирование. Его можно провести в виде самостоятельной работы. В конце изучения всех правил применяется контрольная работа, задания для которой можно подобрать из различных дидактических материалов.
Сложение чисел с разными знаками
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Основные определения
Целые числа — это множество чисел, которые состоят из натуральных чисел, целых отрицательных чисел и нуля.
Положительные целые числа — это целые числа со знаком «плюс». Они всегда больше нуля. Примеры положительных целых чисел: 11, 500, 1387.
У каждого положительного числа есть число-близнец, которое отличается только тем, что перед ним стоит знак минус. Такие числа называются противоположными.
Противоположные числа не равны друг другу, но у них есть общее — модуль. Модуль у противоположных чисел одинаковый: у положительного числа он равен самому числу, а у отрицательного — противоположному, то есть положительному. Например:
Действительные числа — это числа, которые могут быть записаны в виде конечной или бесконечной десятичной дроби.
Рациональные числа — это числа, которые можно представить в виде положительной или отрицательной обыкновенной дроби или числа ноль.
Правило сложения чисел с разными знаками
Положительное число можно рассматривать как доход, а отрицательное — как расходы или долг. Чтобы понять, сколько мы заработали или потратили, нужно смотреть на модули этих чисел.
Например, родители выдали триста рублей на карманные расходы. Если в конце недели у нас осталось немного денег — значит расходов было меньше, чем дохож. А если нам пришлось попросить еще 50 рублей на наклейки — расходы привысили доход. Если же расходы равны доходам, то у нас будет нулевой остаток.
А теперь сформулируем правило сложения чисел с разными знаками.
Чтобы сложить положительное и отрицательное число, нужно:
Это правило сводит сложение чисел с разными знаками к вычитанию из большего положительного числа меньшее число. В результате сложения положительного и отрицательного числа может получиться: положительное число, отрицательное число или нуль.
Повторим еще раз. Чтобы сложить числа с разными знаками:
Алгоритм сложения чисел с разными знаками справедлива для целых чисел, для рациональных чисел и для действительных чисел.
Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.
Примеры сложения чисел с разными знаками
Сложение чисел с разными знаками требует внимательности и последовательности. Рассмотрим примеры по правилу выше:
Нам нужно сложить числа с разными знаками. Выполним все шаги по правилу сложения положительного и отрицательного числа.
Чтобы сложить рациональные числа с разными знаками, которые не являются целыми, их следует представить в виде обыкновенных или десятичных дробей.
Пример 3. Чему равна сумма чисел 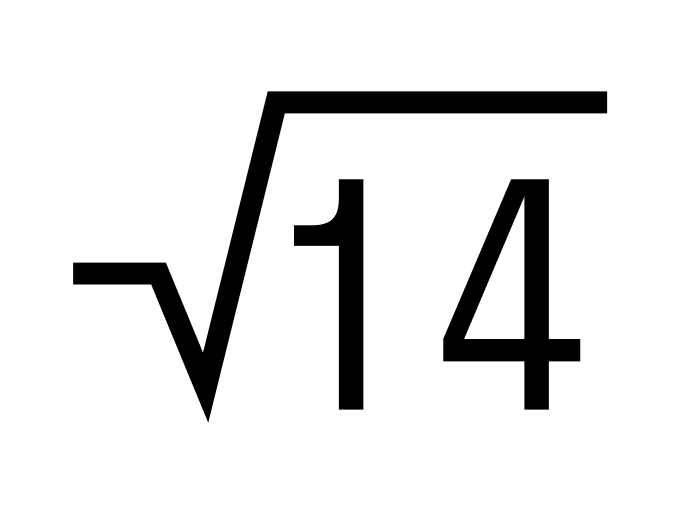
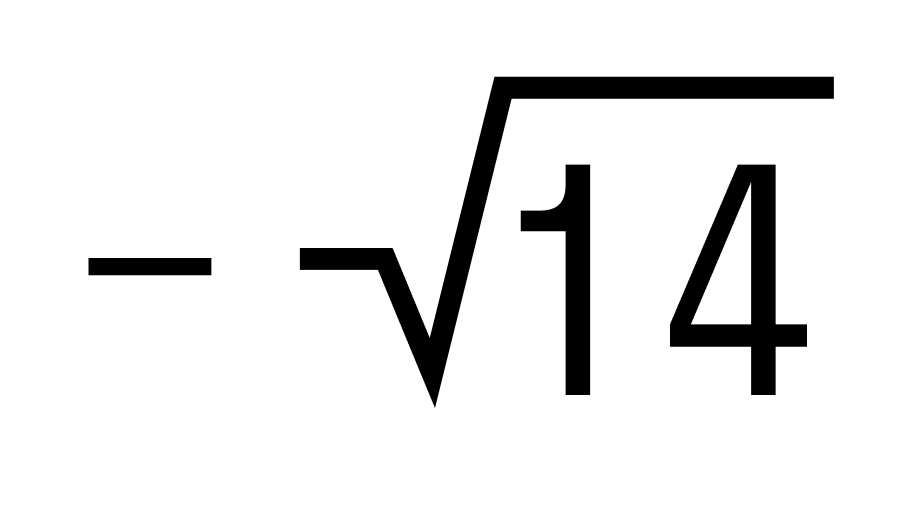
Замечаем, что у складываемых чисел разные знаки, а их модули равны. Значит эти числа являются противоположными, а сумма противоположных чисел равна нулю.
Получается вот так:
Важно помнить, что при сложении действительных чисел с разными знаками результат можно записывать не в виде бесконечной десятичной дроби, а в виде числового выражения, которое содержит корни, степени, логарифмы и прочее.
Математика
Закажи карту Tinkoff Junior сейчас и получи 200 ₽ на счет
С этой картой можно накопить на мечту, жми ⇒
Именная карта банка для детей
с крутым дизайном, +200 бонусов
Закажи свою собственную карту банка и получи бонусы
План урока:
Сложение и вычитание отрицательных чисел
Давайте вспомним любимую многими сказку «Буратино» и разберем задачу с участием любимых персонажей.
Возвращаемся к решению задачи.
Теперь, правильно запишем и суммируем известные данные.
Рассмотрим еще одно задание.
Чтобы вычислить сумму двух значений со знаком «минус», достаточно суммировать их модули, и перед полученной цифрой записать «-».
Запомни! Если складываем два отрицательных числа, то суммируем их модули, а перед результатом сложения записываем «-».
Сложение чисел с разными знаками
Используем рассмотренный алгоритм при выполнении действий.
Суммируем-3 и 10. Для этого:
Помним, что большее значение модуля имеет отрицательное слагаемое (-28), поэтому перед результатом нужно будет поставить знак «минус». Теперь, находим разность большего и меньшего значения модуля (28-17) и записываем математическое выражение:
Учитывая рассмотренные примеры, можно сказать, что:
любое числовое значение от прибавления к нему положительного числа, всегда становится больше, а от прибавления отрицательного числа только меньше.
Докажем справедливость данного правила, вычислив выражение и сравнив уменьшаемое с полученной суммой:-150+50.
Чтобы найти значение выражения нужно определить модули (150 и 50), оставив знак«-» модуля большего слагаемого, от большего значения отнимаем меньшее:
Сравним найденное значение выражения (-100) с уменьшаемым (-150), используя правило сравнения чисел с отрицательным знаком:
При сравнении цифровых значений со знаком «минус», меньшим будет то, чей модуль больше.
-150 1 Сложить их модули, а перед результатом поставить знак «плюс»
Сложение и вычитание отрицательных и положительных чисел — правило, формулы и примеры
Впервые знакомство с отрицательными числами происходит в школьном курсе в 6 классе, иногда раньше. Число со знаком «+» называется положительным, противоположное — отрицательным.
Правило сложения отрицательных чисел и чисел с разными знаками
Для суммирования двух отрицательных чисел, необходимо:
суммировать их модули;
перед полученной суммой поставить знак «минус».
В данном случае, складываем модули 9 и 6, и перед получившимся натуральным числом 15 ставим знак «-«.

Сложение рациональных или дробных чисел выполняется аналогичным способом:
К 26,35 прибавляем 25,35 (т. е. мы складываем модули), в итоге получаем 51,75 с отрицательным значением. Перед ним ставим знак «минус».
Для суммирования натуральных чисел со знаками «+» и «-», надо:
из слагаемого с большим значением модуля вычесть слагаемое с меньшим значением;
перед полученным результатом поставить знак того слагаемого, которое имело большее значение.
61,2 + (-31,5) = + (61,2 — 31,5) = 30,5
Модуль большего числа со знаком «+», соответственно, сумма получилась положительная:
Большее число со знаком «-», поэтому заменяем плюс на минус и получаем отрицательный ответ.
Как вычитать отрицательные и положительные числа
Для нахождения разности противоположных чисел, надо к уменьшаемому прибавить вычитаемое с противоположным знаком, то есть заменить разность суммой.
Наглядно данное действие лучше представить в виде формулы:
То есть любое выражение, содержащее знаки сложения и вычитания, следует решать как сумму чисел.
-6,1 + 5,6 = 5,6 + (-6,3) = 0,5.
Разность выражения будет положительной, если уменьшаемое больше вычитаемого, и отрицательной, если значение модуля уменьшаемого меньше вычитаемого. В случае, когда уменьшаемое и вычитаемое одинаковые, их разность будет равна нулю.
15 — 6 = 15 + (-6) = 9 — уменьшаемое 15, больше вычитаемого, поэтому ответ положительный;
Если нужно отнять отрицательное число, то два знака «минус» подряд дают знак «плюс».
Все вышеперечисленные действия возможно выполнить на калькуляторе. Для этого достаточно ввести сначала модуль числа, потом нажать кнопку изменения знака «+/-».
Заключение
Для закрепления изученных правил можно использовать различные методы проверки знаний. На первом этапе лучшим вариантом будет тренажер, с помощью которого решение подобных примеров можно довести до автоматизма.
Так же для закрепления материала подойдет тестирование. Его можно провести в виде самостоятельной работы. В конце изучения всех правил применяется контрольная работа, задания для которой можно подобрать из различных дидактических материалов.
Объясняем ребенку знаки чисел
Вы уже познакомили первоклашку с отрицательными числами, как я рассказывала в этой статье?
Если да, то сразу же имеет смысл объяснить ребенку, что никакое число никогда не существует само по себе. У него всегда есть знак: плюс или минус.
Удивительное дело, но детям в школе – аж до 4-5 класса – создают какое-то странное представление о том, что знак плюс или минус – это то, что колом вбили между числами.
Вот, даже задания на «вбивание» знаков между числами дают:
Это, кстати, не из Петерсон, где градус безумия и без того зашкаливает, а из уважаемого мной учебника Моро
Ага. А потом у детей создается уродливое представление об устройстве чисел, а мы будем удивляться, что деть отрицательные числа не понимает.
А с чего ребенку их понимать, если он всю жизнь считал знак минус чем-то, что существует само по себе, безотносительно числа.
Числа с ручками
Имеет смысл как можно раньше объяснить малышу, что знаки плюс и минус существуют не сами по себе, а привязаны к числу.
А у числа как будто есть две руки: плюс и минус:
Это числа 1 и 6 с руками 😃 На случай, если я непохоже нарисовала 😃
При помощи этих рук – знаков числа общаются друг с другом.
Одну руку – с одним знаком – число всегда прячет. А вторую – с другим знаком – всегда протягивает вперед, перед собой.
Это число 1 протянуло руку «минус» шестерке. А шестерка протянула единице «плюс»
Если одно число другому протягивает руку с «плюсом», оно как бы говорит: «Прибавь меня».
Если протянуло руку с «минусом» – говорит: «Отними меня».
В нашем примере выше единичка говорит: «Шестерка, я хочу от тебя отняться».
А шестёрка такая: «А я хочу к тебе, единичка, прибавиться».
Поясните для малыша, что – Да, в выражении числа вместе с их знаками можно менять местами. Это потому что благодаря знаку мы знаем, чего «хочет» каждое число.
Попробуем на примере
Теперь возьмите любой длинный пример, и пусть малыш обведет в нем все числа с принадлежащими им «ручками» (рука числа всегда стоит перед «своим» числом):
Мы взяли длинный пример и обвели в нем числа вместе с принадлежащими им ручками
Это на самом деле то же самое, что мы делали в упражнении с огромными числами (я рассказывала в этой статье). Только сейчас мы обвели все числа.
А еще мы дорисовали плюсик (зелёным) к первому числу: потому что, если в первого числа не нарисован знак – значит там плюс.
Теперь можно взять кусочки бумаги и перерисовать на них получившиеся кружочки.
Наш пример, разрезанный на кусочки
А теперь пусть перекладывает кусочки так, как ему удобнее считать. Например, так:
Прибавлять и отнимать 1 и 2 всегда проще, чем шестерки и семерки
Здесь еще проще вычисления
Расскажите малышу, что любой длинный пример из учебника можно посчитать не «подряд» (как пишет наш учебник – “цепочкой”), а удобным способом.
Мы с Сашкой, например, практиковались прямо в учебнике:
Шуркина рабочая тетрадь Петерсон 1 класс, реальные примеры
Видите, кружочками обведено то, что удобнее посчитать в первую очередь.
Кстати, обратите внимание на обведенные в кружочки отрицательные числа. Кто спрашивал, зачем первоклашке отрицательные числа – вот вам один из ответов. Даже первоклашке с отрицательными числами живется гораздо легче, чем без них.