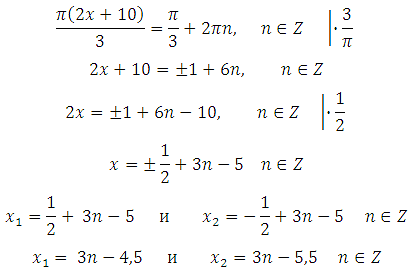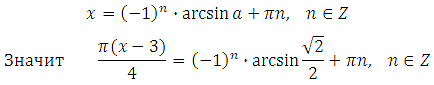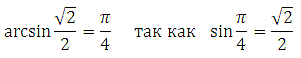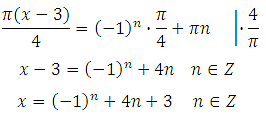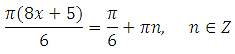Наименьший положительный корень как искать
Нахождение наименьшего положительного корня.
«Управление общеобразовательной организацией:
новые тенденции и современные технологии»
Свидетельство и скидка на обучение каждому участнику
Тема урока: Нахождение наименьшего положительного корня.
— актуализировать знания учащихся по теме «Решение тригонометрических уравнений» и обеспечить их применение при решении задач вариантов ЕНТ;
— рассмотреть общие подходы решения тригонометрических уравнений;
— закрепить навыки решения тригонометрических уравнений;
— познакомить с новыми способами решения тригонометрических уравнений.
— содействовать развитию у учащихся мыслительных операций: умение анализировать, синтезировать, сравнивать;
— формировать и развивать общеучебные умения и навыки: обобщение, поиск способов решения;
— вырабатывать внимание, самостоятельность при работе на уроке;
— способствовать формированию активности и настойчивости, максимальной работоспособности.
а) 

б) 

а) 

б) 

а) 

б) 

а) 

III . Работа по отработке умений решать тригонометрические уравнения (работа у доски и в тетрадях )
Найти корни заданного уравнения на заданном промежутке:
а) 

Нетрудно видеть, что простым перебором по параметру n мы сразу получаем все требуемые корни уравнения, т.е.:
Ответ: 
1.Решите уравнение 
2. Найти наименьший положительный корень уравнения sinx + sin 5 x = 0.
3.Найдите наименьший положительный корень уравнения cosx + cos 5 x = 0
А. π/6 В. π/4 Б. π/2 Г. π
4. Из Абитуриента №26 Найдите наименьшее решение уравнения sinx = 
5. Найдите наименьшее решение уравнения cos = 
Отбор корней в тригонометрическом уравнении из ЕГЭ по математике
Одно из заданий второй части ЕГЭ по математике — решение тригонометрических уравнений с корнем. Основная его сложность в том, что нужно уметь не только упрощать выражения и находить ответ, но и проводить отбор корней. Как это сделать, мы разберем в статье.
Что такое тригонометрическое уравнение
Тригонометрическое уравнение содержит в себе функцию синуса, косинуса, тангенса или котангенса. Решение без отбора корней происходит по следующим формулам:
sinx = a при |a| ≤ 1 → x = (-1) n arcsina + πn;
cosx = a при |a| ≤ 1 → x = ± arccosa + 2πn;
tgx = b при b — любое число → x = arctgb + πn;
сtgx = b при b — любое число → x = arcсtgb + πn.
Отбор
Прежде чем изучить методы отбора корней, решим один несложный пример.
Первое слагаемое распишем по формуле косинуса двойного угла:
Приведем однородные слагаемые:
Пусть cosx = t, где |t| ≤ 1
x 1 = 3+ 1 2 2 = 4 4 =1
x 2 = 3- 1 2 2 = 2 4 = 1 2
Возвращаемся к исходной переменной и получаем:
cosx = 1 → x = 2πn, n ∈ Z
cosx = ½ → x = ± π/3 + 2πk, k ∈ Z
Области допустимых значений нет, поэтому оба значения используем при решении пункта «б».
Теперь проведем отбор корней разными способами.
Арифметический
Для решения нужно перебирать все значения целочисленного параметра и считать корни. Разберем на примере cosx = 1.
Далее то же самое нужно сделать с остальными корнями. Тогда вы получите ответ.
Алгебраический
Чтобы отобрать корни, нужно решить неравенства относительно известного целочисленного параметра. Рассмотрим на примере первого значения.
Делим все части неравенства на «2π»:
Геометрический
Рисуем единичную окружность, наносим на нее числа из области и корни. После определяем, попадают ли они в промежуток. Отсчет промежутка происходит против часовой стрелки!
Функционально-графический
Как видно по рисунку, у нас получаются те же корни, что и в предыдущем методе.
Теперь вы знаете основные способы отбора корней в тригонометрических уравнениях. Это поможет вам правильно решать задания из второй части. Дома вам сложно практиковаться, не хватает помощи учителя? Тогда записывайтесь на курсы подготовки к ЕГЭ в центре «Уникум» при Российском университете дружбы народов. Центр предлагает не только полезные уроки с экспертами ЕГЭ, но и доступ к учебному порталу. На нем вы сможете делать домашние задания, решать пробные варианты экзамена и изучать полезные материалы. Форматы курсов разные — очный и дистанционный.
Содержание данной статьи носит ознакомительный характер. Для подготовки к сдаче ЕГЭ пользуйтесь дополнительными источниками информации!
Тригонометрические уравнения
Тригонометрические уравнения. В составе экзамена по математике в первой части имеется задание связанное с решением уравнения — это простые уравнения, которые решаются за минуты, многие типы можно решить устно. Включают в себя: линейные, квадратные, рациональные, иррациональные, показательные, логарифмические и тригонометрические уравнения.
В этой статье мы рассмотрим тригонометрические уравнения. Их решение отличается и по объёму вычисления и по сложности от остальных задач этой части. Не пугайтесь, под словом «сложность», имеется виду их относительную сложность по сравнению с другими заданиями.
Кроме нахождения самих корней уравнения, необходимо определить наибольший отрицательный, либо наименьший положительный корень. Вероятность того, что вам на экзамене попадёт тригонометрическое уравнение, конечно же, мала.
Их в данной части ЕГЭ менее 7%. Но это не означает, что их нужно оставить без внимания. В части С тоже необходимо решить тригонометрическое уравнение, поэтому хорошо разобраться с методикой решения и понимать теорию просто необходимо.
Понимание раздела «Тригонометрия» в математике во многом определяет ваш успех при решении многих задач. Напоминаю, что ответом является целое число или конечная десятичная дробь. После того, как получите корни уравнения, ОБЯЗАТЕЛЬНО сделайте проверку. Много времени это не займёт, а вас избавит от ошибки.
В будущем мы также рассмотрим и другие уравнения, не пропустите! Вспомним формулы корней тригонометрических уравнений, их необходимо знать:
Знание этих значений необходимо, это «азбука», без которой невозможно будет справиться с множеством заданий. Отлично, если память хорошая, вы легко выучили и запомнили эти значения. Что делать, если этого сделать не получается, в голове путаница, да просто вы именно при сдаче экзамена сбились. Обидно будет потерять бал из-за того, что вы запишите при расчётах неверное значение.
Алгоритм восстановления этих значений прост, он также приведён в теории, полученной вами во втором письме после подписки на рассылку. Если ещё не подписались, сделайте это! В будущем также рассмотрим, как эти значения можно определить по тригонометрической окружности. Не даром её называют «Золотое сердце тригонометрии».
Сразу поясню, во избежание путаницы, что в рассматриваемых ниже уравнениях даны определения арксинуса, арккосинуса, арктангенса с использованием угла х для соответствующих уравнений: cosx=a, sinx=a, tgx=a, где х может быть и выражением. В примерах ниже у нас аргумент задан именно выражением.
Итак, рассмотрим следующие задачи:
Найдите корень уравнения:
В ответе запишите наибольший отрицательный корень.
Решением уравнения cos x = a являются два корня:
Определение: Пусть число a по модулю не превосходит единицы. Арккосинусом числа a называется угол x, лежащий в пределах от 0 до Пи, косинус которого равен a.
Найдём наибольший отрицательный корень. Как это сделать? Подставим различные значения n в полученные корни, вычислим и выберем наибольший отрицательный.
Общая рекомендация для всех подобных задач: для начала берите диапазон n от – 2 до 2. Если требуемое значение выявить не удалось, подставляем следующие значения x: – 3 и 3, – 4 и 4 и так далее.
При n = – 2 х1= 3 (– 2) – 4,5 = – 10,5 х2= 3 (– 2) – 5,5 = – 11,5
При n = – 1 х1= 3 (– 1) – 4,5 = – 7,5 х2= 3 (– 1) – 5,5 = – 8,5
При n = 0 х1= 3∙0 – 4,5 = – 4,5 х2= 3∙0 – 5,5 = – 5,5
При n = 1 х1= 3∙1 – 4,5 = – 1,5 х2= 3∙1 – 5,5 = – 2,5
При n = 2 х1= 3∙2 – 4,5 = 1,5 х2= 3∙2 – 5,5 = 0,5
Получили, что наибольший отрицательный корень равен –1,5
В ответе напишите наименьший положительный корень.
Решением уравнения sin x = a являются два корня:
Либо (он объединяет оба указанные выше):
Определение: Пусть число a по модулю не превосходит единицы. Арксинусом числа a называется угол x, лежащий в пределах от – 90 о до 90 о синус которого равен a.
Выразим x (умножим обе части уравнения на 4 и разделим на Пи):
Найдём наименьший положительный корень. Здесь сразу видно, что при подстановке отрицательных значений n мы получим отрицательные корни. Поэтому будем подставлять n = 0,1,2 …
При n = 0 х = (– 1) 0 + 4∙0 + 3 = 4
При n = 1 х = (– 1) 1 + 4∙1 + 3 = 6
При n = 2 х = (– 1) 2 + 4∙2 + 3 = 12
Проверим при n = –1 х = (–1) –1 + 4∙(–1) + 3 = –2
Значит наименьший положительный корень равен 4.
В ответе напишите наименьший положительный корень.
Решением уравнения tg x = a является корень:
Выразим x (умножим обе части уравнения на 6 и разделим на Пи):
Найдём наименьший положительный корень. Подставим значения n = 1,2,3. Отрицательные значения подставлять нет смысла, так как видно, что получим отрицательные корни:
Таким образом, наименьший положительный корень равен 0,25.
Определение котангенса: Арккотангенсом числа a (a – любое число) называется угол x принадлежащий интервалу (0;П), котангенс которого равен a.
Здесь хочу добавить, что в уравнениях в правой части может стоять отрицательное число, то есть тригонометрическая функция от аргумента может иметь отрицательное значение. Если в ходе решения вы не сможете определить угол, например, для
то данные формулы вам помогут:
Спасибо за внимание, учитесь с удовольствием!