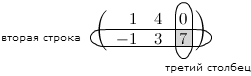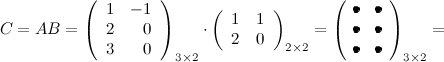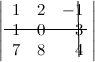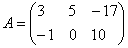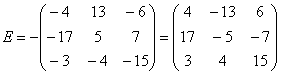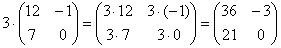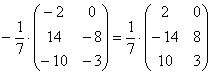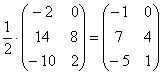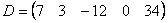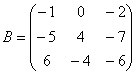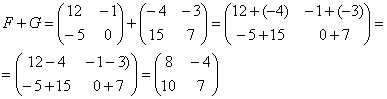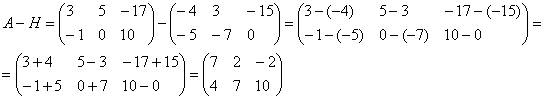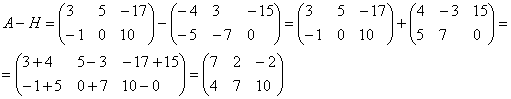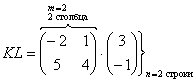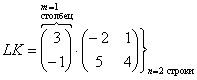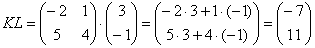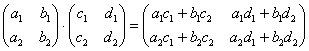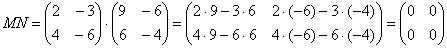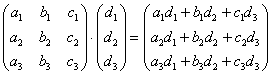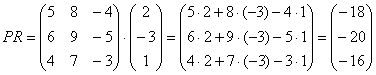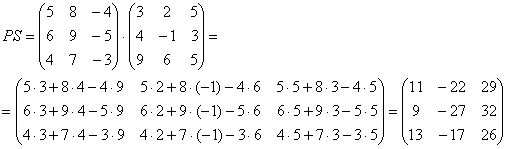Матрицы математика как решать примеры
Примеры решения задач с матрицами
Матрицы широко применяются в математике для компактной записи СЛАУ или систем дифференциальных уравнений. Тогда количество строк матрицы соответствует количеству уравнений системы, а количество столбцов равно количеству неизвестных. Матричный аппарат позволяет свести решение громоздких СЛАУ к компактным операциям над матрицами.
На практике, они позволяют не делать лишних операций и сократить время выполнения задач. Поэтому, будущим специалистам очень важно понять теорию матриц и научиться решать задачи с ними. Перед изучением примеров решения задач советуем изучить теоретический материал по матрицам, прочитать все определения и свойства. Список тем находится в правом меню.
Примеры по темам:
Матрицы: основные определения и понятия
Решение. Находим элемент, который стоит на пересечении второй строки и третьего столбца:
Умножение матрицы на число
Примеры решения задач с матрицами не по зубам? Тебе ответит эксперт через 10 минут!
Сложение и вычитание матриц
Умножение матриц
Выполним произведения в более компактном виде:
Транспонирование матрицы
Минор и алгебраическое дополнение
Решение. Вычеркиваем в заданном определителе вторую строку и третий столбец:
Вычисление определителя
$+3 \cdot 3 \cdot 1-(-1) \cdot 1 \cdot 1-3 \cdot(-2) \cdot 3-4 \cdot 3 \cdot(-2)=54$
Решение. Выполним следующие преобразования над строками определителя: из второй строки отнимем четыре первых, а из третьей первую строку, умноженную на семь, в результате, согласно свойствам определителя, получим определитель, равный данному.
Определитель равен нулю, так как вторая и третья строки являются пропорциональными.
Далее из третьей строки выносим (-10) за определитель и делаем нули в третьем столбце под главной диагональю, а для этого к последней строке прибавляем третью:
Нахождение обратной матрицы
От первой строки отнимаем вторую (для этого от элемента первой строки отнимаем соответствующий элемент второй строки):
От второй строки отнимаем две первых:
Первую и вторую строки меняем местами:
От второй строки отнимаем две первых:
Вторую строку умножаем на (-1), а к первой строке прибавляем вторую:
Итак, слева получили единичную матрицу, а значит матрица, стоящая в правой части (справа от вертикальной черты), является обратной к исходной.
Решение. Вычисляем определитель матрицы:
$\Delta=\left| \begin
$-1 \cdot(-1) \cdot 2-3 \cdot 1 \cdot 1-2 \cdot 0 \cdot(-1)=1+12+0+2-3+0=12 \neq 0$
Транспонируем эту матрицу (т.е. строки матрицы делаем столбцами с тем же номером):
Нахождение ранга матрицы
Меняем местами первую и вторую строчки:
Далее четвертую и первую строки:
так как содержит два пропорциональных столбца (первый и второй); второй минор
преобразуем следующим образом: к первой строке прибавим третью, а ко второй две третьих:
И так как первая и вторая строки пропорциональны, то минор равен нулю.
Матрицы: примеры с решением и объяснением
Вы будете перенаправлены на Автор24
Матрицы представляют собой таблицы чисел, взаимосвязанных между собой. Над ними возможно проводить ряд разнообразных операций, о которых мы расскажем вам ниже.
Сложение и вычитание
Итак, о сложении и вычитании. Эти действия возможно проводить только с матрицами одинакового размера.
Для того чтобы осуществить эти действия, необходимо провести сложение или вычитание каждого элемента матрицы с элементом другой матрицы, стоящим на той же позиции, что элемент в первой.
Готовые работы на аналогичную тему
Обратите внимание, что сложение и вычитание для матриц возможно осуществлять только если их порядки одинаковые.
Объяснение:
Умножение матрицы на число
Произведение матричных таблиц
Эта задача несколько сложнее предыдущих, но при этом в ней также нет ничего сложного.
Математически это можно записать так:
Если число столбцов первого матричного множителя не совпадает с количеством строчек второго матричного множителя, то умножение выполнить невозможно.
$A \times B = \begin
Нахождение определителя матрицы
Детерминант возможно найти только для квадратных разновидностей матриц.
Вычислить определитель от матрицы порядка двух можно следуя такому правилу:
Определитель матрицы размера 2 равен разности произведений элементов, стоящих на главной диагонали с произведением элементов с побочной диагонали:
Для определителей большего размера можно использовать преобразования Гаусса и разложение по строчке.
Обратные матрицы
Получить обратную матрицу.
Решение:
$ \begin
Теперь обнуляем последний элемент первой строчки. Для этого к верхней строчке плюсуем нижнюю:
Транспонирование матричных таблиц
Решение:
Применим метод Саррюса для детерминанта:
Мы получили вырожденную матрицу.
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 15 05 2021
Примеры решения матриц с ответами
Простое объяснение принципов решения матриц и 10 наглядных примеров. В каждом примере поэтапный ход решения и ответ.
Алгоритм решения матриц
Матрица – это математическая таблица с числовыми значениями. Обозначаются матрицы латинскими буквами.
Есть два отличия между матрицами:
С матрицей можно выполнять самые наипростейшие действия: умножение, деление, сложение, вычитание и трансформация.
Сложение и вычитание
Данные действия можно совершать тогда, когда матрицы равны между собой, чтобы в конце получилось выражение аналогичной размерности. Сложение и вычитание выполняются по аналогии друг друга.
Задание
Даны две матрицы, найдите их сумму.
Решение
Элемент первой строки складывается с элементом второй. Абсолютно также совершается вычитание, только вместо плюса, нужно поставить минус.
Задание
Даны две матрицы, найдите их разность.
Решение
Задание
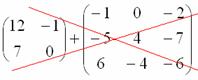
Найдите C=2A +3B, если :
Решение
Нужна помощь в написании работы?
Умножение
В математике умножать таблицу с числами можно абсолютно любую. В таком случае число умножается с показателем. Умножаем первое число на первой строке с числом второго столбца и так далее.
Задание
Даны две матрицы. Умножьте их друг на друга.
Решение
Матрицы можно перемножать друг на друга, только если количество столбцов в первой матрице, равно количеству строк второй. Элемент матрицы будет равняться сумме произведений (Aji), где i – строки в таблице; j – строки чисел второй таблицы.
Возведение матрицы в степень
Данную формулу используют лишь в случаях, если матрица стоит в квадратном выражении. Важно знать, что степень должна быть у таких выражений натуральной!
Если число не будет натуральным, то это усложняет возведение матрицы в степень, так как степень n придётся умножить саму на себя n количество раз. Но если у Вас такой случай, то используется следующая формула.
Задание
Решение
В первую очередь найдём, для этого нужно будет просто умножить её саму на себя.
После по формуле подставляем числовые значения.
Расчёт определителя
В математике линейной есть два понятия – определитель и детерминант. Определитель – это какое-либо число, которое ставится в соответствии с квадратной матрицей. Определитель используется при решении многих задач. Найти его можно с помощью формулы.
А детерминант находиться с помощью перемножения простых матриц, используются числа только с побочной и главной диагоналях.
Есть вероятность, что произведения матрицы будут значительно отличаться друг от друга. Если индекс чётный, то число будет со знаком плюс, если нечётный, то число будет со знаком минус. Обозначается определитель det А, а круглые скобки меняются на квадратные.
Дано
Решение
Пользуемся свойствам степеней – A^<3>=A^<2>*A
Далее используем свойство степеней
Ответ
Задание
Найдите определитель матрицы А.
Решение
Обратная матрица
Перед тем, как речь непосредственно пойдёт о самой обратной связи матрицы, давайте разберём алгоритм трансформирования матрицы. Во время трансформации столбцы и строки меняются местами.
Задание
Найти обратную матрицу А.
Решение
Приписываем к матрице А матрицу третьего ряда.
Переводим всё в единичную матрицу.
Ответ
Обратная матрица
Обратная матрица схожа с алгоритмом нахождения обратных чисел. К примеру, если умножить матричную таблицу на обратную матрицу, то в итоге мы получаем A*A(-1)=E. Но чтобы перейти уже к нахождению обратной матрицы, нам придётся найти её определитель. Мы рассмотрим самый простой способ – алгебраических дополнений.
Задание
В пример возьмём квадратную матрицу, она находиться с помощью следующей формулы:
-транспортированные матрицы;|А| – определитель.
Рассмотрим самый простейший пример, где размер таблицы 2*2.
Найти обратную матрицу
Решение
Для начала находим определитель матрицы.
Подставляем числа, возвращаясь к матрица, которая указана выше.
Всегда начинаем с левого верхнего угла и делаем следующее:
← линиями показано, что нужно и как зачеркнуть.
Как итог, у нас остаётся число 4
Теперь мы переходим к нахождению алгебраических дополнений.
Первым делом нужно поменять знаки у двух чисел в мироне.
← подчёркнуты те числа, у которых мы будем менять знаки.
, вот что у нас получилось.
И наконец-то мы переходим к завершающему этапу, к нахождению транспортированной матрице.
, вспоминаем формулу нахождения, и подставляем числовые значения
В завершении желательно проверить правильно ли мы нашли числовую таблицу. Это делать не обязательно, но рекомендуется, чтобы удостовериться в том, то ответ верный.
Задание
Решение
Начинаем с определения матрицы.
Дело осталось за малым – осталось начти алгебраическое дополнение матрицы А:
Действия с матрицами
Данное методическое пособие поможет Вам научиться выполнять действия с матрицами: сложение (вычитание) матриц, транспонирование матрицы, умножение матриц, нахождение обратной матрицы. Весь материал изложен в простой и доступной форме, приведены соответствующие примеры, таким образом, даже неподготовленный человек сможет научиться выполнять действия с матрицами. Для самоконтроля и самопроверки Вы можете бесплатно скачать матричный калькулятор >>>.
Я буду стараться минимизировать теоретические выкладки, кое-где возможны объяснения «на пальцах» и использование ненаучных терминов. Любители основательной теории, пожалуйста, не занимайтесь критикой, наша задача – научиться выполнять действия с матрицами.
Для СВЕРХБЫСТРОЙ подготовки по теме (у кого «горит») есть интенсивный pdf-курс Матрица, определитель и зачёт!
Матрица – это прямоугольная таблица каких-либо элементов. В качестве элементов мы будем рассматривать числа, то есть числовые матрицы. ЭЛЕМЕНТ – это термин. Термин желательно запомнить, он будет часто встречаться, не случайно я использовал для его выделения жирный шрифт.
Обозначение: матрицы обычно обозначают прописными латинскими буквами
Пример: рассмотрим матрицу «два на три»:
Данная матрица состоит из шести элементов: 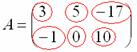
Все числа (элементы) внутри матрицы существуют сами по себе, то есть ни о каком вычитании речи не идет: 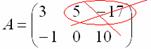
Это просто таблица (набор) чисел!
Также договоримся не переставлять числа, если иного не сказано в объяснениях. У каждого числа свое местоположение, и перетасовывать их нельзя!
Рассматриваемая матрица имеет две строки: 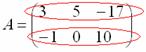
и три столбца:
СТАНДАРТ: когда говорят о размерах матрицы, то сначала указывают количество строк, а только потом – количество столбцов. Мы только что разобрали по косточкам матрицу «два на три».
Если количество строк и столбцов матрицы совпадает, то матрицу называют квадратной, например: 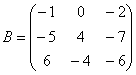
Если в матрице один столбец 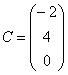
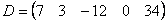
На самом деле понятие матрицы мы знаем еще со школы, рассмотрим, например точку с координатами «икс» и «игрек»: 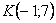
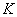
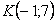
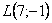
Теперь переходим непосредственно к изучению действий с матрицами:
1) Действие первое. Вынесение минуса из матрицы (внесение минуса в матрицу).
Вернемся к нашей матрице 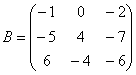
Вынесем минус за пределы матрицы, сменив у КАЖДОГО элемента матрицы знак: 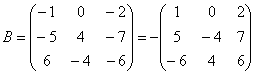
У нуля, как Вы понимаете, знак не меняется, ноль – он и в Африке ноль.
Обратный пример: 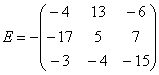
Внесем минус в матрицу, сменив у КАЖДОГО элемента матрицы знак:
Ну вот, гораздо симпатичнее получилось. И, самое главное, выполнять какие-либо действия с матрицей будет ПРОЩЕ. Потому что есть такая математическая народная примета: чем больше минусов – тем больше путаницы и ошибок.
2) Действие второе. Умножение матрицы на число.
Всё просто, для того чтобы умножить матрицу на число, нужно каждый элемент матрицы умножить на данное число. В данном случае – на тройку.
Еще один полезный пример:
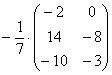
Сначала рассмотрим то, чего делать НЕ НАДО: 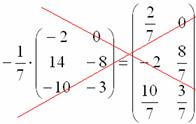
Вносить дробь в матрицу НЕ НУЖНО, во-первых, это только затрудняет дальнейшие действия с матрицей, во-вторых, затрудняет проверку решения преподавателем (особенно, если 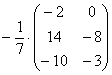
И, тем более, НЕ НАДО делить каждый элемент матрицы на минус семь:
Из статьи Математика для чайников или с чего начать, мы помним, что десятичных дробей с запятой в высшей математике стараются всячески избегать.
Единственное, что желательно сделать в этом примере – это внести минус в матрицу:
А вот если бы ВСЕ элементы матрицы делились на 7 без остатка, то тогда можно (и нужно!) было бы поделить.
В этом случае можно и НУЖНО умножить все элементы матрицы на 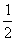
Примечание: в теории высшей математики школьного понятия «деление» нет. Вместо фразы «это поделить на это» всегда можно сказать «это умножить на дробь». То есть, деление – это частный случай умножения.
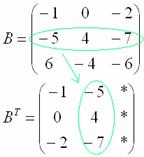
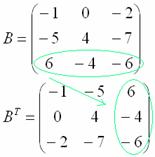
3) Действие третье. Транспонирование матрицы.
Для того чтобы транспонировать матрицу, нужно ее строки записать в столбцы транспонированной матрицы.
Транспонировать матрицу
Строка здесь всего одна и, согласно правилу, её нужно записать в столбец:
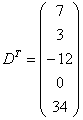
Транспонированная матрица обычно обозначается надстрочным индексом 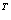
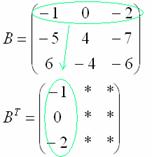
Транспонировать матрицу
Сначала переписываем первую строку в первый столбец:
Потом переписываем вторую строку во второй столбец:
И, наконец, переписываем третью строку в третий столбец:
Готово. Образно говоря, транспонировать – это значит взять матрицу за правый верхний угол и аккуратно повернуть её «на себя» по диагонали, «стряхивая» числа в столбцы транспонированной матрицы. Такая вот у меня ассоциация.
4) Действие четвертое. Сумма (разность) матриц.
Сумма матриц действие несложное.
НЕ ВСЕ МАТРИЦЫ МОЖНО СКЛАДЫВАТЬ. Для выполнения сложения (вычитания) матриц, необходимо, чтобы они были ОДИНАКОВЫМИ ПО РАЗМЕРУ.
Например, если дана матрица «два на два», то ее можно складывать только с матрицей «два на два» и никакой другой!
Сложить матрицы 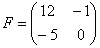
Для того чтобы сложить матрицы, необходимо сложить их соответствующие элементы:
Для разности матриц правило аналогичное, необходимо найти разность соответствующих элементов.
Найти разность матриц 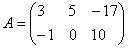
А как решить данный пример проще, чтобы не запутаться? Целесообразно избавиться от лишних минусов, для этого внесем минус в матрицу 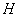
Примечание: в теории высшей математики школьного понятия «вычитание» нет. Вместо фразы «из этого вычесть это» всегда можно сказать «к этому прибавить отрицательное число». То есть, вычитание – это частный случай сложения.
5) Действие пятое. Умножение матриц.
Чем дальше в лес, тем толще партизаны. Скажу сразу, правило умножения матриц выглядит очень странно, и объяснить его не так-то просто, но я все-таки постараюсь это сделать, используя конкретные примеры.
Какие матрицы можно умножать?
Чтобы матрицу 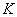
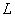
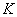
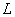
Пример:
Можно ли умножить матрицу 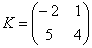
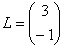
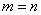
А вот если матрицы переставить местами, то, в данном случае, умножение уже невозможно!
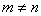
Не так уж редко встречаются задания с подвохом, когда студенту предлагается умножить матрицы, умножение которых заведомо невозможно.
Следует отметить, что в ряде случаев можно умножать матрицы и так, и так.
Например, для матриц, 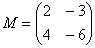
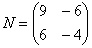
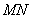
Как умножить матрицы?
Умножение матриц лучше объяснить на конкретных примерах, так как строгое определение введет в замешательство (или помешательство) большинство читателей.
Начнем с самого простого:
Умножить матрицу 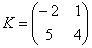
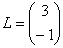
Я буду сразу приводить формулу для каждого случая:
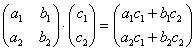
Умножить матрицу 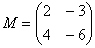
Формула:
В результате получена так называемая нулевая матрица.
Попробуйте самостоятельно выполнить умножение 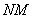
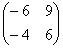
Обратите внимание, что 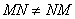
Таким образом, при умножении переставлять матрицы нельзя!
Если в задании предложено умножить матрицу 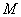
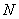
Переходим к матрицам третьего порядка:
Умножить матрицу 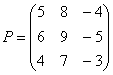
Формула очень похожа на предыдущие формулы:
А теперь попробуйте самостоятельно разобраться в умножении следующих матриц:
Умножьте матрицу 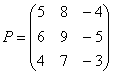
Вот готовое решение, но постарайтесь сначала в него не заглядывать!
Данная тема достаточно обширна, и я вынес этот пункт на отдельную страницу.
А пока спектакль закончен.
После освоения начального уровня рекомендую отработать действия с матрицами на уроке Свойства операций над матрицами. Матричные выражения.
Автор: Емелин Александр
(Переход на главную страницу)

cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5