Матлаб как построить график функции

Построение графиков функций

Здравствуйте! В этой статье мы разберем построение графиков на MATLAB для различных математических функций, а также научимся выводить несколько графиков одновременно.

Где прописывать код

Графики MATLAB

Построение графиков функций в MATLAB можно реализовать разными способами, например, через plot или polar, с полным списком можете ознакомиться здесь.
Но сейчас речь пойдёт о функции ezplot.
Разберём такой пример:

Открываем скрипт и пишем нехитрый код:

Вывод:

На этом примере мы видим, как работает функция ezplot(), где в качестве аргументов указывается функция без ‘y=’ и интервал значений в квадратных скобках. Чтобы построить два графика в одном окне используем hold on. А axis tight — устанавливает границы осей в диапазоне данных значений.
Разберём ещё один:

Его скорее всего проще записать в компилятор напрямую.
Давайте ещё один:

И последний:

В данном случае мы указали границы оси с помощью axis от -π до π.

Если остались вопросы по поводу построения графиков функций в MATLAB, то обязательно пишите в комментариях, ответим.

Источник

Строим графики в MATLAB

Первая и самая часто встречающаяся функция это plot(. ), параметры умышленно не пишу, сейчас будем в них разбираться.

Во-первых, стоит разделить реализации на две основные группы. Первая из них принимает два параметра plot(x, y), еслимы обозначим ось абсцисс за X, а ось ординат за Y, то наша функция последовательно наставит нам на координатной плоскости точек и единственным требованием к массивам х и у будет равенство их длин. Возьмем 4 случайные точки и построим их.

В итоге получаем следующую ломаную:

Массив ординат тот же, что и ранее, но результат уже другой.

Иногда автомасштабирование графика может нас неустроить и мы захотим свои пределы отображения по осям. Для примера я поставлю пределы по больше, чтобы было видно разницу.

Если нужно включить сетку, то можно воспользоваться командой grid on, за одно давайте сменим функцию на какую-нибудь более красивую.

Отмечу также, что можно занять несколько ячеек разметки одним графиком. Теперь вернемся к вопросу построения нескольких кривых в одних осях координат. Строить будем в одном окне сразу оба по этому применим subplot. Будем строить один под другим, соответственно у нас получится subplot(2, 1, 1) и subplot(2, 1, 2).

Первый метод это подставить в plot несколько пар значений plot(x₁,y₁,x₂,y₂) второй способ применить команду hold on. Посмотрим на код и результат его работы.

Вот и настал тот момент, когда возникает вопрос: «А что на Вашем графике есть что?», чтобы он не возникал давайте научимся подписывать графики, настраивать параметры линий, отображать «легенду». Про параметры линий я скажу пару слов отдельно, а все остальное покажу в коде и там же подробно прокомментирую.

При задании спецификации линий существует два типа нотаций укорченная и полная, например, цвет можно задать параметром ‘color’ или сокращенно первой буквой от названия цвета.

Отлично, с вопросом разобрались. Теперь построим все по красоте, а одну из линий нашпигуем по полной. Относительно предыдущего примера у нас появятся заголовки, подписи осей, параметры линий, а также на втором графике оставим только одну линию.

Отдельно скажу, что есть еще метод суперзаголовка, но похоже он в одном из тулбоксов и в чистом MATLAB не доступен.

Источник

Матлаб как построить график функции

Обычная графика MATLAB

Построение графиков точками и отрезками прямых

Графики в логарифмическоми полулогарифмическом масштабе

Гистограммы и диаграммы

Графики специальных типов

Создание массивов данных для трехмерной графики

Построение графиков трехмерных поверхностей, сечений и контуров

Средства управления подсветкой и обзором фигур

Средства оформления графиков

Одновременный вывод нескольких графиков

Управление цветовой палитрой

Окраска трехмерных поверхностей

Двумерные и трехмерные графические объекты

Одно из достоинств системы MATLAB — обилие средств графики, начиная от команд построения простых графиков функций одной переменной в декартовой системе координат и кончая комбинированными и презентационными графиками с элементами анимации, а также средствами проектирования графического пользовательского интерфейса (GUI). Особое внимание в системе уделено трехмерной графике с функциональной окраской отображаемых фигур и имитацией различных световых эффектов.

Описанию графических функций и команд посвящена обширная электронная книга в формате PDF. Объем материала по графике настолько велик, что помимо вводного описания графики в уроке 3 в этой книге даются еще два урока по средствам обычной и специальной графики. Они намеренно предшествуют систематизированному описанию большинства функций системы MATLAB, поскольку графическая визуализация вычислений довольно широко используется в последующих материалах книги. При этом графические средства системы доступны как в командном режиме вычислений, так и в программах. Этот урок рекомендуется изучать выборочно или выделить на него не менее 4 часов.

Построение графиков отрезками прямых

Функции одной переменной у(х) находят широкое применение в практике математических и других расчетов, а также в технике компьютерного математического моделирования. Для отображения таких функций используются графики в декартовой (прямоугольной) системе координат. При этом обычно строятся две оси — горизонтальная X и вертикальная Y, и задаются координаты х и у, определяющие узловые точки функции у(х). Эти точки соединяются друг с другом отрезками прямых, т. е. при построении графика осуществляется линейная интерполяция для промежуточных точек. Поскольку MATLAB — матричная система, совокупность точек у(х) задается векторами X и Y одинакового размера.

Команда plot служит для построения графиков функций в декартовой системе координат. Эта команда имеет ряд параметров, рассматриваемых ниже.

plot (X, Y) — строит график функции у(х), координаты точек (х, у) которой берутся из векторов одинакового размера Y и X. Если X или Y — матрица, то строится семейство графиков по данным, содержащимся в колонках матрицы.

Приведенный ниже пример иллюстрирует построение графиков двух функций — sin(x) и cos(x), значения функции которых содержатся в матрице Y, а значения аргумента х хранятся в векторе X:

На рис. 6.1 показан график функций из этого примера. В данном случае отчетливо видно, что график состоит из отрезков, и если вам нужно, чтобы отображаемая функция имела вид гладкой кривой, необходимо увеличить количество узловых точек. Расположение их может быть произвольным.

Рис. 6.1. Графики двух функций в декартовой системе координат

plot(Y) — строит график у(г), где значения у берутся из вектора Y, a i представляет собой индекс соответствующего элемента. Если Y содержит комплексные элементы, то выполняется команда plot (real (Y). imag(Y)). Во всех других случаях мнимая часть данных игнорируется.

Вот пример использования команды plot(Y):

Соответствующий график показан на рис. 6.2.

Рис. 6.2. График функции, представляющей вектор Y с комплексными элементами

plot(X.Y.S) — аналогична команде plot(X.Y), но тип линии графика можно задавать с помощью строковой константы S.

Значениями константы S могут быть следующие символы.

Источник

Матлаб как построить график функции

Основы графической визуализации вычислений

Особенности графики системы MATLAB

Построение графика функций одной переменной

Построение трехмерных графиков

Вращение графиков мышью

Контекстное меню графиков

Управление форматом графиков

Особенности графики системы MATLAB

Начиная с версии MATLAB 4.0, впервые ориентированной на Windows, графические средства системы MATLAB были существенно улучшены. Основные отличительные черты графики в новой версии MATLAB 6:

существенно улучшенный интерфейс графических окон;

введение новой панели инструментов Camera для интерактивного изменения условий видимости объекта;

расширенные возможности форматирования графики;

возможность создания графики в отдельных окнах;

возможность вывода нескольких графических окон;

возможность перемещения окон по экрану и изменения их размеров;

возможность перемещения области графики внутри графического окна;

задание различных координатных систем и осей;

высокое качество графики;

широкие возможности использования цвета;

легкость установки графических признаков — атрибутов;

снятие ограничений на число цветов;

обилие параметров команд графики;

возможность получения естественно выглядящих трехмерных фигур и их сочетаний;

простота построения трехмерных графиков с их проекцией на плоскость;

возможность построения сечений трехмерных фигур и поверхностей плоскостями;

функциональная многоцветная и полутоновая окраска;

возможность имитации световых эффектов при освещении фигур точечным источником света;

возможность создания анимационной графики;

возможность создания объектов для типового интерфейса пользователя.

С понятием графики связано представление о графических объектах, имеющих определенные свойства. В большинстве случаев об объектах можно забыть, если только вы не занимаетесь объектно-ориентированным программированием задач графики. Связано это с тем, что большинство команд высокоуровневой графики, ориентированной на конечного пользователя, автоматически устанавливает свойства графических объектов и обеспечивает воспроизведение графики в нужных системе координат, палитре цветов, масштабе и т. д.

На более низком уровне решения задач используется ориентированная на программиста дескрипторная графика (Handle Graphics), при которой каждому графическому объекту в соответствие ставится особое описание — дескриптор, на который возможны ссылки при использовании графического объекта. Дескрипторная графика позволяет осуществлять визуальное программирование объектов пользовательского интерфейса — управляющих кнопок, текстовых панелей и т. д. Команды дескрипторной графики могут использоваться в высокоуровневой графике, например, для удаления осей, изменения цвета и т. д. в уже построенных графических объектах. Эти обширные возможности делают графику MATLAB одной из лучших среди графических подсистем систем компьютерной математики (СКМ).

Несмотря на обилие графических команд, их синтаксис достаточно прост и легко усваивается даже начинающими пользователями. Руководствуясь правилом описания «от простого к сложному», мы рассмотрим сначала графику функций одной переменной, а затем трехмерную графику, специальную, анимационную и, наконец, дескрипторную.

Хотя данная книга не предусматривает исчерпывающе полного описания всех команд графики системы MATLAB, большинство команд графики будет рассмотрено с примерами, которые можно считать дополнительными к тем, которые приведены в документации по системе.

Построение графика функций одной переменной

В режиме непосредственных вычислений доступны практически все возможности системы. Широко используется, например, построение графиков различных функций, дающих наглядное представление об их поведении в широком диапазоне изменения аргумента. При этом графики строятся в отдельных масштабируемых и перемещаемых окнах.

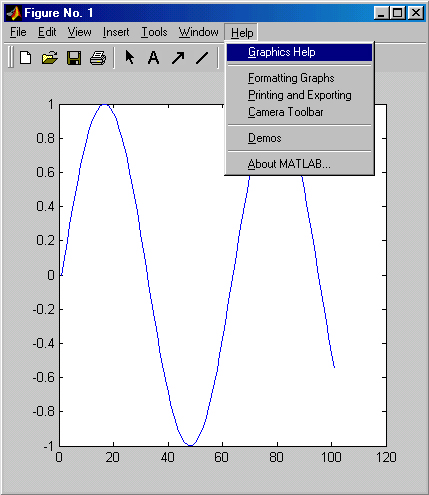
Возьмем вначале простейший пример — построение графика синусоиды. Следует помнить, что MATLAB (как и другие СКМ) строит графики функций по ряду точек, соединяя их отрезками прямых, т. е. осуществляя линейную интерполяцию функции в интервале между смежными точками. Зададим интервал изменения аргумента х от 0 до 10с шагом 0.1. Для построения графика достаточно вначале задать вектор х=0:0.1:10, а затем использовать команду построения графиков plot(sin(x)). Это показано на рис. 3.1.

Вектор х задает интервал изменения независимой переменной от 0 до 10 с шагом 0.1. Почему взят такой шаг, а не, скажем, 1? Дело в том, что plot строит не истинный график функции sin(x), а лишь заданное числом элементов вектора х число точек. Эти точки затем просто соединяются отрезками прямых, т. е. осуществляется кусочно-линейная интерполяция данных графика. При 100 точках полученная кривая глазом воспринимается как вполне плавная, но при 10-20 точках она будет выглядеть состоящей из отрезков прямых.

Графики MATLAB строит в отдельных окнах, называемых графическими окнами. С первого взгляда видны отличия графического окна, показанного на рис. 3.1, от командного окна MATLAB. В главном меню окна появилась позиция Tools (Инструменты), которая позволяет вывести или скрыть инструментальную панель, видимую в верхней части окна графики на рис. 3.1. Средства этой панели (мы их рассмотрим полнее в дальнейшем) позволяют легко управлять параметрами графиков и наносить на них текстовые комментарии в любом месте.

Рис. 3.1. Пример построения графика синусоиды

Построение в одном окне графиков нескольких функций

Более подробное описание графического окна будет дано в уроке 5. А пока пойдем дальше и попытаемся построить графики сразу трех функций: sin(x), cos(#) и sin (x)/х. Прежде всего отметим, что эти функции могут быть обозначены переменными, не имеющими явного указания аргумента в виде у(х):

»yl=sin(x): y2=cos(x): y3=sin(x)/x;

Такая возможность обусловлена тем, что эти переменные являются векторами — как и переменная х. Теперь можно использовать одну из ряда форм команды

где al, а2, аЗ,.„ — векторы аргументов функций (в нашем случае все они — х), a f1, f2, f3. —векторы значений функций, графики которых строятся в одном окне. В нашем случае для построения графиков указанных функций мы должны записать следующее:

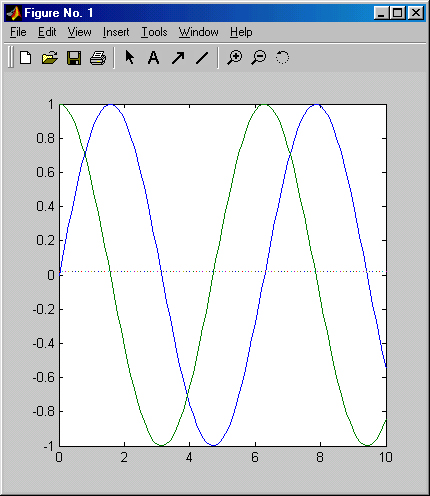
Можно ожидать, что MATLAB в этом случае построит, как обычно, точки графиков этих функций и соединит их отрезками линий. Но, увы, если мы выполним эти команды, то никакого графика не получим вообще. Не исключен даже сбой Б работе программы. Причина этого казуса уже обсуждалась в предыдущем уроке — при вычислении функции y3=sin(x)/x, если х представляет собой массив (вектор), то нельзя использовать оператор матричного деления /.

Рис. 3.2. Построение графиков трех функций

Обратите внимание на то, что хотя на этот раз MATLAB построил графики всех трех функций, в окне командного режима появилось предупреждение о делении на 0 — в момент, когда х=0. Это говорит о том, что pi ot «не знает» о том, что неопределенность sin(x)/x=0/0 устранимая и дает 1. Это недостаток практически всех систем для численных вычислений.

Графическая функция fplot

Разумеется, MATLAB имеет средства для построения графиков и таких функций, как sin(x)/x, которые имеют устранимые неопределенности. Не обсуждая эти средства подробно, просто покажем, как это делается, с помощью другой графической команды —

fplot: fplott’f(x)’. [xmin xmax])

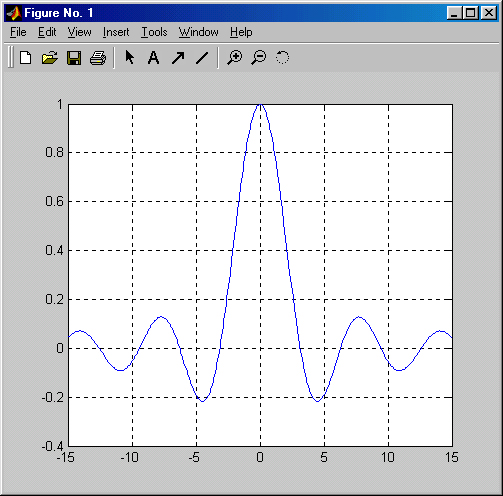
Она позволяет строить функцию, заданную в символьном виде, в интервале изменения аргумента х от xmin до xmax без фиксированного шага изменения х. Один из вариантов ее применения демонстрирует рис. 3.3. Хотя в процессе вычислений предупреждение об ошибке (деление на 0) выводится, но график строится правильно, при х=0 sinx/x=l. Обратите также внимание на две используемые команды: clear (очистить)— очистка графического окна и grid on (сетка)— включение отображения сетки, которая строится пунктирными линиями.

Рис. 3.3. Построение графика sin(x)/x функцией fplot

На рис. 3.3 представлено также меню File (Файл) окна графики. Нетрудно заметить, что оно содержит типовые файловые операции. Однако они относятся не к файлам документов, а к файлам графиков. В частности, можно присваивать имя записываемым на диск рисункам с графиками.

Позже мы более подробно рассмотрим возможности различных графических команд. В частности, покажем, как можно задавать определенный цвет и стиль линий, как менять вывод координатных осей, наносить на графики различные текстовые надписи и выполнять множество иных операций форматирования графиков для придания им более наглядного вида, соответствующего требованиям пользователя. Мы также обсудим множество новых форм применения графических команд, резко расширяющих их возможности построения графиков всех мыслимых типов.

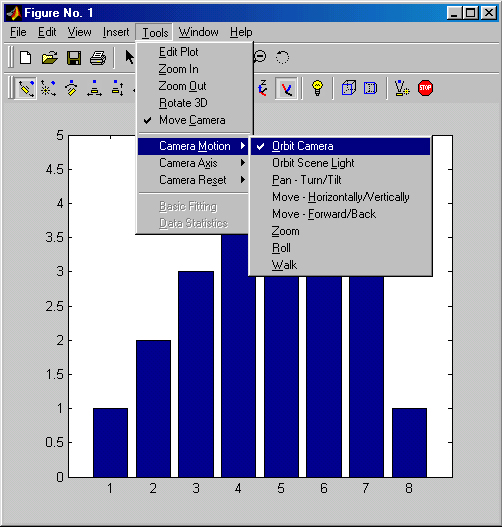
В прикладных расчетах часто встречаются графики, именуемые столбцовыми диаграммами, отражающие содержание некоторого вектора V. При этом каждый элемент вектора представляется столбцом, высота которого пропорциональна значению элемента. Столбцы нумеруются и масштабируются по отношению к максимальному значению наиболее высокого столбца. Выполняет построение такого графика команда bar(V) (рис. 3.4).

Столбцовые диаграммы — лишь один из многих типов графиков, которые может строить система MATLAB. Особенно часто столбцовые диаграммы используются при представлении данных финансово-экономических расчетов.

Рис. 3.4 дает также представление о меню Tools (Инструменты) окна графики, появившемся начиная с версии MATLAB 5.3.1 (выпуск 11.1). Нетрудно заметить, что кроме возможности вывода инструментальной панели здесь имеется целый ряд других команд, которые будут рассмотрены в дальнейшем. Это команды вывода свойств графических объектов, изменения масштаба графика, добавления осей и т. д.

Рис. 3.4. Построение столбцовой диаграммы значений элементов вектора

Построение трехмерных графиков

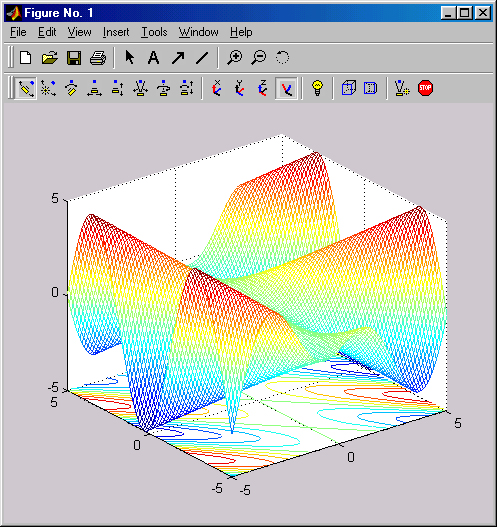
Столь же просто обеспечивается построение графиков сложных поверхностей. Надо только знать, какой командой реализуется тот или иной график. Например, для построения графика поверхности и ее проекции в виде контурного графика на плоскость под поверхностью достаточно использовать следующие команды (см. урок 6):

Окно с построенным графиком показано на рис. 3.5.

Рис. 3.5. Окно с графиками поверхности и ее проекции на плоскость под фигурой

Мы ограничимся этими примерами построения графиков как достаточно простыми и типовыми. Из них следует важный вывод — для решения той или иной частной задачи надо знать соответствующие команды и функции. В этом вам помогут как данная книга, так и справочная система MATLAB.

Вращение графиков мышью

Можно поворачивать построенную фигуру мышью и наблюдать ее под разными углами. Рассмотрим эту возможность на примере построения логотипа системы MATLAB — мембраны. Для этого, введя команду membrane, получим исходный график, представленный на рис. 3.6.

Рис. 3.6. Построение мембраны — логотипа системы MATLAB

Для вращения графика достаточно активизировать последнюю справа кнопку панели инструментов с изображением пунктирной окружности со стрелкой. Теперь, введя курсор мыши в область графика и нажав левую кнопку мыши, можно круговыми движениями заставить график вращаться вместе с обрамляющим его параллелепипедом (рис. 3.7).

Любопытно, что в версии MATLAB 6 вращать можно и двумерные графики, наблюдая поворот плоскости, в которой они построены. Никакого программирования такое вращение не требует.

Рис. 3.7. Вращение трехмерной фигуры мышью

Контекстное меню графиков

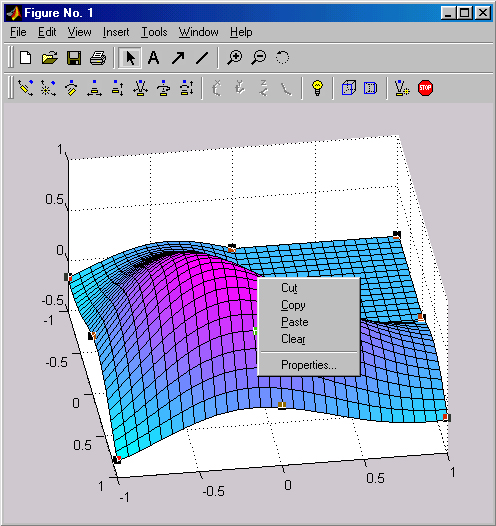
Для переключения в режим редактирования графика нужно щелкнуть на кнопке Edit Plot (Редактировать график) с изображением курсора-стрелки. В этом режиме графиком можно управлять с помощью контекстного меню, вызываемого щелчком правой кнопки мыши. Вид этого меню при курсоре, расположенном в области трехмерного графика вне построенных трехмерных графических объектов, показан на рис. 3.8. С помощью мыши можно также выделить график. Щелчок левой клавишей выводит рамку вокруг рисунка (см. рис. 3.8). Теперь на график можно наносить стрелки, поясняющие надписи (кнопка с буквой А) и т. д.

Рис. 3.8. График в состоянии редактирования и контекстное меню

Основы форматирования двумерных графиков

Графики в системе MATLAB строятся обманчиво просто. Связано это с тем, что многие свойства графиков установлены по умолчанию. К таким свойствам относятся вывод или скрытие координатных осей, положение их центра, цвет линии графика, ее толщина и т. д. и т. п. Позже будет показано, как свойства и вид графиков можно менять в широких пределах с помощью параметров команд графики. Однако этот путь требует хорошего знания деталей языка программирования и дескрипторной графики системы MATLAB.

В новой версии MATLAB 6 для изменения свойств графиков (их форматирования) используются принципы визуального контроля за стилем (видом) всех объектов графиков. Это позволяет легко, просто и наглядно придать графикам должный вид перед записью их в виде файлов на диск. Можно сказать, что в этой части реализованы отдельные принципы визуально-ориентированного программирования графических средств.

Здесь мы рассмотрим возможности форматирования графиков, которые, образно говоря, лежат на поверхности. Систематизированное описание интерфейса системы MATLAB 6.0, в том числе интерфейса графических окон, дается в уроке 5.

Форматирование линий графиков

MATLAB имеет возможность легко настраивать и корректировать свойства графиков с помощью специальных средств. В новой версии MATLAB 6.0 они существенно изменены. Так, в предшествующей версии для настройки (форматирования) графиков использовался специальный редактор свойств — Graphics Properties Editor (Редактор свойств графики). Его можно было вызвать из меню File окна командного режима MATLAB с помощью команды Show Graphics Properties Editor (Показать редактор свойств графики).

В новой версии MATLAB форматирование графиков стало более строгим и удобным. При этом ранее упомянутый редактор свойств графиков перестал так именоваться, и команда Show Graphics Properties в новой версии отсутствует. Ее заменяют команды Figure Properties (свойства фигуры) и Axis Properties (свойства осей) со всеми необходимыми настройками.

При построении графиков появляется графическое окно. Иногда оно бывает скрыто ранее имеющимися окнами как системы MATLAB, так и других работающих в среде Windows 95/98/Me/2000/NT4 приложений. Если вы не увидели графика, заданного для построения, то поищите его в списке открытых окон (приложений), нажимая клавиши Alt + Tab, и выберите из списка нужное окно. Окна графики имеют изображение логотипа системы MATLAB. По умолчанию они выводятся с панелью инструментов с рядом кнопок вполне очевидного назначения.

Щелкнув на кнопке Edit Plot (Редактировать график) в панели инструментов окна графики и щелкнув по графику, можно заметить, что график выделился: вокруг него появилась рамка. Теперь, указав курсором мыши на тот или иной объект графика и щелкнув снова левой клавишей, можно наблюдать выделение объекта и появление окна его форматирования.

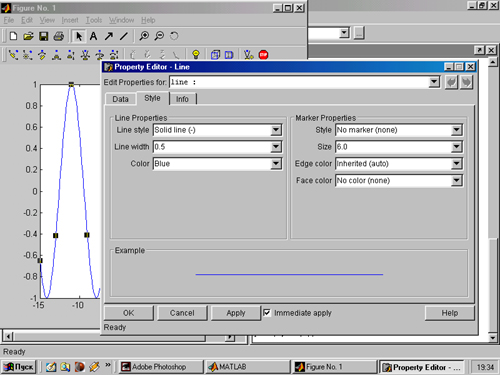
Например, указав в режиме редактирования мышью на линию графика (и дважды быстро щелкнув левой клавишей), можно увидеть окно форматирования линий графика, показанное на рис. 3.9 слева. Часть окна графики с выделенным графиком видна справа. Обратите внимание на появление на линии графика ряда черных квадратиков, — они используются для указания курсором мыши именно на линию графика, а не на другие объекты.

Рис. 3.9. Окно графика (справа) и окно форматирования линий (слева)

В этом окне открыта главная для операций форматирования вкладка — Style (Стиль). Она устанавливает стиль отображения линии, т. е. ее вид (например, сплошная линия или пунктирная), ширину и цвет, а также параметры маркеров, отмечающих опорные точки графиков.

Полезно знать, что кнопка Apply (Применить) позволяет применить сделанные установки к графику до закрытия окна диалога. Кнопка О К вводит сделанные установки и закрывает окно диалога. Назначение других кнопок очевидно.

Форматирование маркеров опорных точек

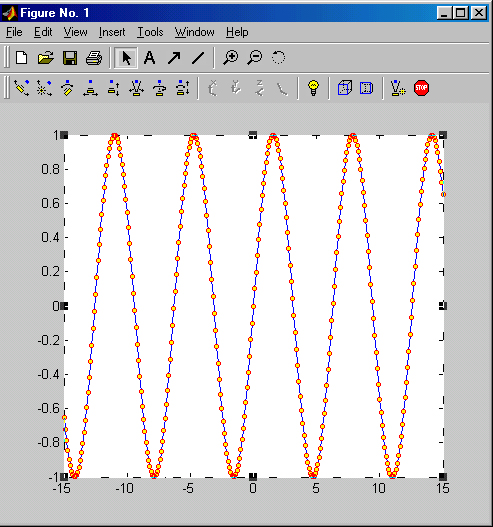
Рис. 3.10. Пример задания параметров маркеров и построения графика с ними

Можно задавать размеры маркеров, цвет их закраски и цвет окантовки. Так, на рис. 3.10 при его просмотре на экране цветного дисплея маркеры имеют вид окружностей с условным размером 4, цветом окантовки красным и цветом закраски желтым. Маркеры можно задавать в виде окружностей, прямоугольников, крестиков, ромбиков и т. д. Применение маркеров делает графики более наглядными.

Форматирование линий и маркеров для графика нескольких функций

Если строится график нескольких функций, то можно форматировать линии и маркеры каждой кривой отдельно. Выполним следующие команды:

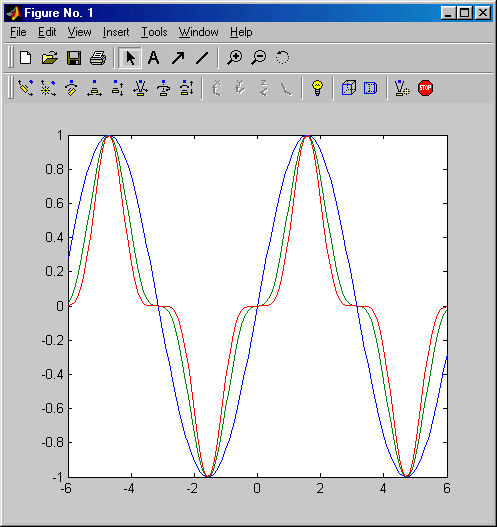
Рис. 3.11 показывает пример такого форматирования для графика, полученного исполнением этих команд.

Кстати, обратите внимание на то, как заданы степени синуса. Записать эти выражения в виде sin(x)^2 и cos(x)^2 будет грубейшей ошибкой, поскольку х здесь вектор. Операторы ^ в данном случае дают поэлементное возведение в степень, что и нужно для построения графиков этих функций.

Рис. 3.11. Пример форматирования для графика трех функций

Форматирование осей графиков

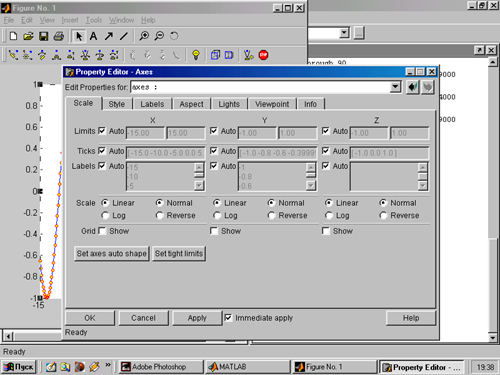
Аналогично описанным выше правилам выполняется форматирование и других объектов графиков. Например, указав курсором мыши на оси графиков (на них тоже есть метки в виде черных квадратиков) и дважды щелкнув левой клавишей мыши, можно увидеть появление окна форматирования объектов дескрипторной графики Property Editor (Редактор свойств, Графический редактор свойств) (рис. 3.12), настроенного на форматирование осей.

Рис. 3.12. Пример форматирования осей графика

Окно графического редактора свойств дескрипторной графики имеет множество вкладок, настройки которых довольно очевидны, и ничто не мешает читателю поэкспериментировать с ними несколько минут. Это позволит понять простоту и одновременно высокую эффективность средств форматирования объектов графики. Например, вы можете задать линейный или логарифмический масштаб осей (вкладка Scale (Масштаб), открытая на рис. 3.12), нормальное или инверсное направление осей ( X, У, а в случае трехмерных графиков и Z), показ сетки (параметр Grid Show), изменить стиль осей и цвета фона (вкладка Style (Стиль)), нанести у осей надписи (вкладка Label (Ярлык)) и пр.

Рис. 3.13 показывает график синусоиды после некоторых операций по форматированию осей. Здесь (кстати, как и на рис. 3.12) задано построение сетки Grid по осям X и Y, построение надписей (просто буквы X и Y) по координатным осям и построение титульной надписи. Заодно на рис. 3.13 показано в открытом виде меню расширенных инструментальных средств графического окна. Его команды подробно обсуждаются в уроке 5. Словом, с объектами графики можно сделать все, что угодно! Некоторые из возможностей форматирования объектов графики мы рассмотрим позже, по мере описания типов графиков.

Рис. 3.13. Пример построения графика синусоиды после форматирования осей

Если компьютер оснащен должным набором шрифтов, то надписи на графиках могут быть сделаны на русском языке — рис. 3.13 хорошо иллюстрирует эту важную для наших пользователей возможность. На нем титульная надпись сделана на русском языке. Средства форматирования надписей дают обширные возможности по выбору набора шрифтов, их стиля, размеров символов и их цвета.

Нанесение надписей и стрелок прямо на график

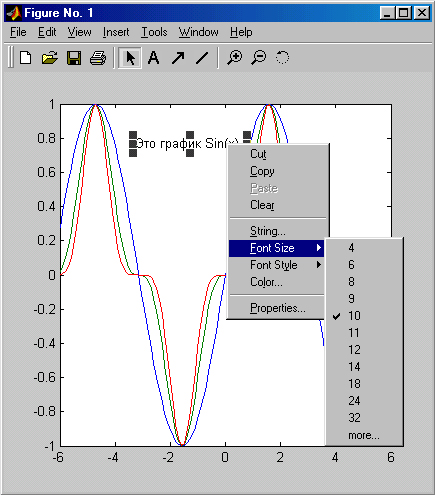
Дополнительно на график можно нанести надписи с помощью кнопки панели инструментов с буквой А. Место надписи фиксируется щелчком мыши. На рис. 3.14 показан отформатированный график с текстовым блоком, созданным таким образом в левой верхней части поля графика.

Здесь показано контекстное меню правой клавиши мыши, поясняющее выбор размера символов надписи (и другие возможности этого меню). Напоминаем, что это меню появляется при щелчке правой кнопки мыши на заданном объекте. В этом меню имеются все команды, доступные для данного объекта в данной ситуации.

Рис. 3.14. Нанесение надписи на отформатированный график

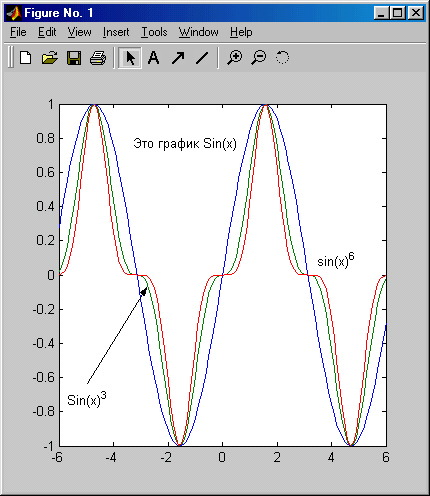
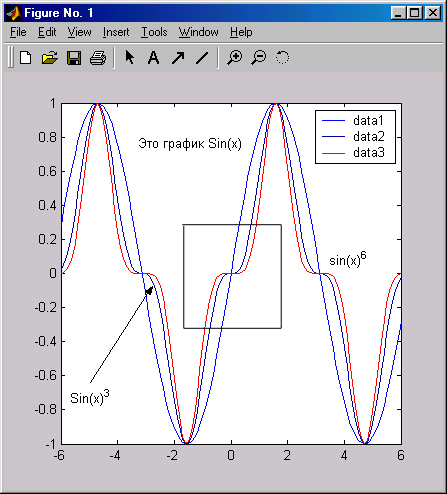
Полученную таким образом надпись можно выделить и перенести мышью в любое другое место. Рис. 3.15 показывает процесс создания еще двух надписей с переносом их текстового блока в нужное место. Надписи сделаны с разным размером символов и разным стилем. Особенно приятно, что при задании на надписи возведения в степень знаком ^ надпись на экране отображается в естественном математическом виде (степень в виде верхнего индекса).

Рис. 3.15. Окончательно отформатированный график трех функций

На рис. 3.15, в частности, показано задание надписей разным стилем, а также задание стрелки с помощью соответствующей кнопки панели инструментов. Это стрелку в режиме редактирования графика можно перемещать и вращать мышью, а также менять ее длину. Можно также наносить на график и обычные линии (без стрелки).

Построение легенды и шкалы цветов на графике

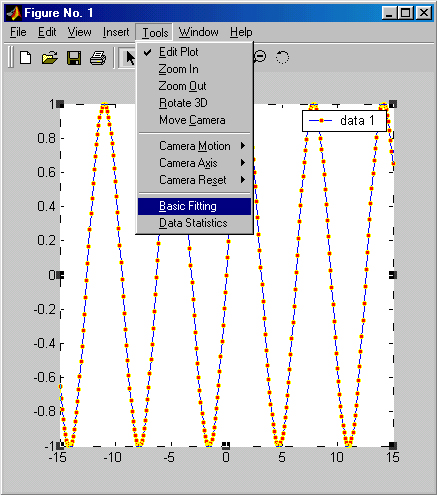
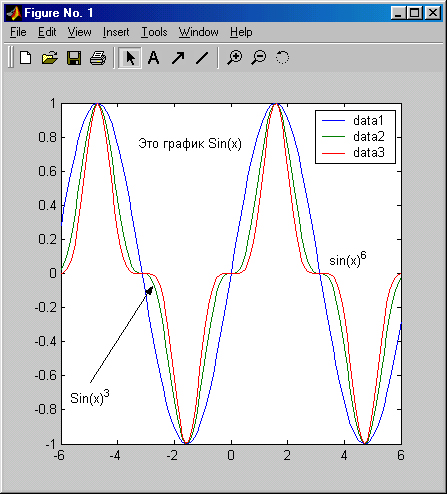
Дополнительно можно изменить размеры графика (см. меню Tools (Инструменты) и его команды Zoom In (Увеличить)и Zoom Out (Уменьшить)), начать поворот графика мышью (команда Rotate 3D), добавить отрезок прямой или иной графический примитив (подменю Add) и подключить к графику легенду — пояснение в виде отрезков линий со справочными надписями, размещаемое внутри графика или около него. Поскольку наш график содержит три кривые, то легенда представляет собой обозначение этих трех линий в правом верхнем углу рисунка (рис. 3.16). Каждая линия имеет тот же цвет, что и на графике (и тот же стиль).

Рис. 3.16. Окончательно сформированный график

Следует еще раз отметить, что все описанные возможности форматирования графиков доступны и программным способом, путем задания соответствующих графических команд, параметров и примитивов. Например команда text(х,у, ‘legend’) позволяет задать надпись ‘legend’ с началом, имеющим координаты (х, у). Если после первого апострофа перед текстом поместить параметр \leftarrow, то надпись (легенда) появится после стрелки с острием, обращенным влево. Аналогично параметр \rightarrow после надписи задает вывод стрелки после надписи с острием, обращенным вправо. Эта возможность позволяет помечать не только кривые, но и отдельные точки на них. Возможно также применение команды legend(‘s1’, ‘s2’. ), выводящей легенду обычного вида — отрезки линий графиков с поясняющими надписями ‘si’, ‘s2’ и т.д.

Перемещение графика в графическом окне

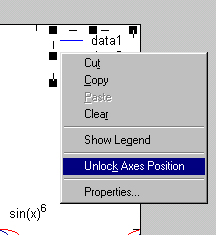
Обычно график занимает фиксированное положение в центре графического окна. Однако в режиме редактирования графиков, когда курсор мыши находится в области графика, в контекстном меню правой клавиши мыши есть команда Unlock Axes Position (Отключить позиционирование осей). Она снимает фиксацию положения координатных осей графика и позволяет двигать его мышью вместе с осями. Это иллюстрирует рис. 3.17.

Рис. 3.17. Пример перемещения графика

Интересно, что при перемещении графика его легенда и цветовая диаграмма остаются на прежнем месте.

Применение графической «лупы»

Рис. 3.18. Пример выделения части графика

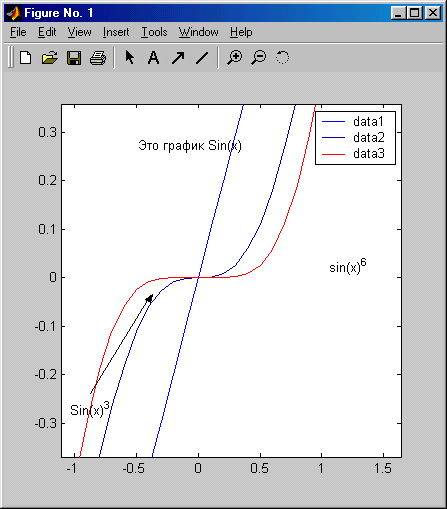
Рис. 3.19. Пример просмотра части графика

Область выделения отмечается прямоугольником из тонких точечных линий. Отпустив левую клавишу мыши, можно наблюдать построение выделенной части графика на всем окне — рис. 3.19. С помощью команды Zoom Out можно восстановить график в прежнем масштабе. Таким образом реализуется графическая «лупа».

Работа с камерой 3D-графики

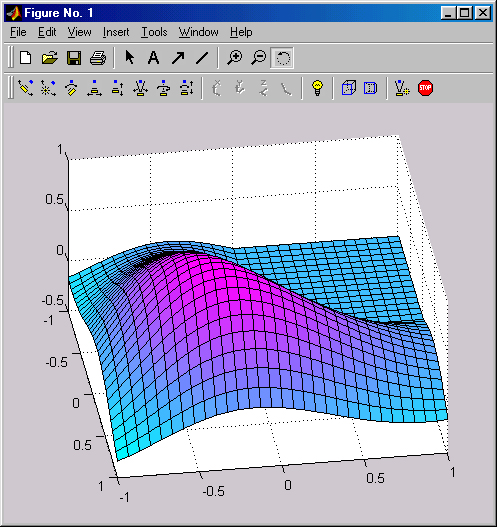
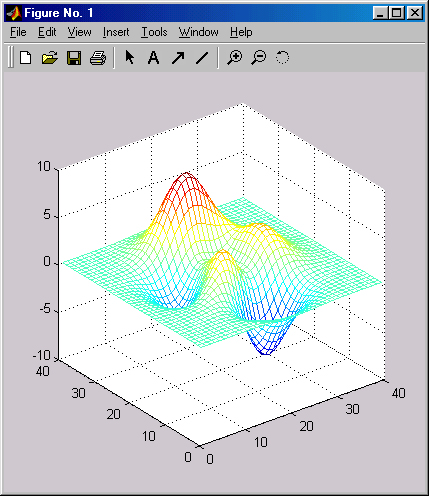
В отличие от двумерных (2D) графиков форматирование трехмерных графиков содержит ряд дополнительных возможностей. Покажем их на простом примере построения 3D-графики с помощью следующих простых команд:

Рис. 3.20. Пример построения каркасного 3D-графика

Здесь первая команда создает массив точек поверхности с помощью одного из ряда встроенных в ядро системы MATLAB готовых описаний таких поверхностей.

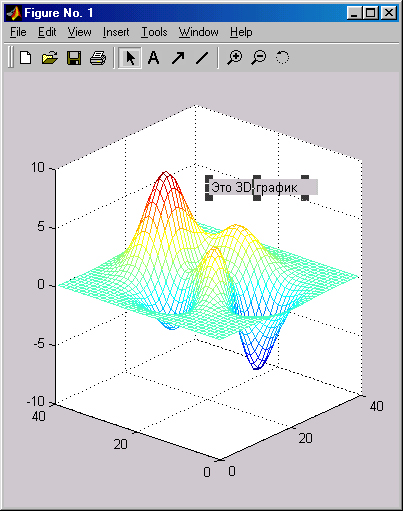
Рис. 3.21. Пример форматирования трехмерного графика

Вторая команда просто строит эту поверхность по опорным точкам с использованием интерполяции для промежуточных точек. Таким образом создается цветная каркасная поверхность, как бы сотканная из разноцветных проволок. На рис. 3.20 показано построение этой поверхности вместе со специальной панелью инструментов трехмерной графики, названной в оригинале Camera (Камера).

Несмотря на множество кнопок, пользование панелью инструментов 3D-графики достаточно просто, если представить себе, что вы смотрите на предмет через объектив фотокамеры. Наглядные рисунки на кнопках поясняют смысл их действия — это перемещение и вращение 3D-рисунков относительно тех или иных координатных осей, включение отображения перспективы, изменение цветовой схемы и др.

Рис.. 3.22. Cтоп кадр вращения трехмерного графика

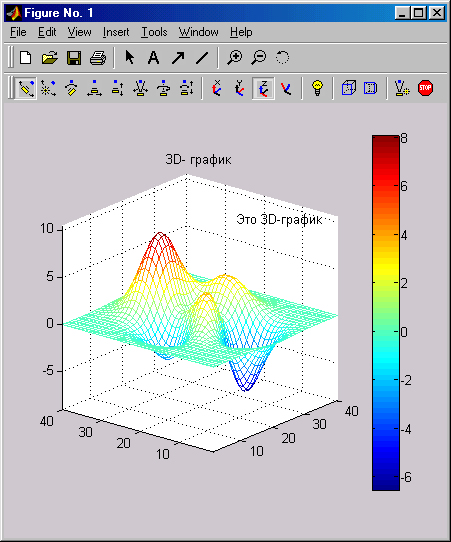
Рис. 3.21 показывает, что приемы форматирования двумерной графики можно использовать при работе с трехмерной графикой — вывод надписи на график, вывод легенды (кстати, теперь объемной) и шкалы цветов.

Для управления положением и вращением трехмерного графика можно использовать клавиши перемещения курсора. Эффект вращения графика иллюстрирует рис. 3.22, где показан график рис. 3.21 после его поворота при нажатой клавише —>. В отличие от поворота мышью (также возможного) перемещение и повороты с помощью клавиш курсора при выбранном типе перемещения дают плавное перемещение или вращение фигуры. Таким образом осуществляется анимация (оживление) трехмерной графики.

Заключительные замечания по графике

Итак, мы рассмотрели основные приемы форматирования графиков, в основном используя средства панели инструментов и отдельные, достаточно очевидные, команды из меню графического окна. Более подробно интерфейс пользователя графического окна будет описан в уроке 5.

Хотя многие приемы форматирования графики заимствованы из технологии визуально-ориентированного программирования, в базовой системе MATLAB (без дополнительных пакетов расширения (toolbox)) все еще отсутствует полноценная возможность такого программирования, даже с учетом расширенных возможностей дескрипторной графики. Это видно уже из того, что вносимые форматированием изменения в графиках не сопровождаются генерацией программных кодов, которые в последующем при их вызове с новыми параметрами порождали бы построение графиков с новыми параметрами. Пользователь может лишь записать на диск копии созданных графиков в формате растрового изображения (.bmp) и использовать их в целях иллюстрации своих материалов.

Однако средства MATLAB позволяют опытным программистам создать расширения системы с визуально-ориентированной технологией программирования. Самым наглядным примером этого является система моделирования динамических объектов Simulink с набором моделей из готовых блоков. При этом автоматически создается не только сложная графическая блок-схема моделируемого устройства, но и система уравнений состояния, решение которой и является основой моделирования.

Источник