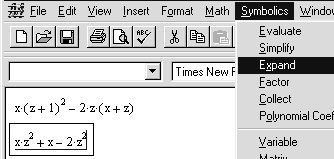
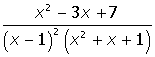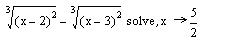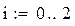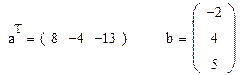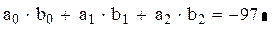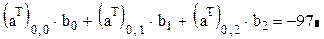Как вывести результат в маткаде
3.1.6. Символьный вывод в MathCAD
Чтобы попытаться вычислить символьно математическое выражение, например В • sin(arcsin(С • Х)), где В,С,Х — некоторые переменные:
Рис. 3.4. Кнопка вставки оператора символьного вывода
Листинг 3.10. Символьный вывод выражения
Листинг 3.11. Символьный вывод выражений, которое не удалось упростить
Присмотритесь внимательнее к листингам 3.10 и 3.11: для символьного вывода не требуется предварительно определять переменные, входящие в левую часть выражения! Если же переменным были все-таки присвоены ранее некоторые значения, символьный процессор просто подставит их в упрощенную формулу и выдаст результат с учетом этих значений (см. в качестве примера два следующих листинга — 3.12 и 3.13).
Точно так же, как рассчитываются численно значения функций, можно вычислять их и с помощью символьного процессора. Сравните соответствующие результаты, которые представлены в листинге 3.12 (конечно, символьный и численный ответы равны: 9•cos(8)=-1.31). Аналогично можно «символьно выводить значения переменных. Например, присвоить некоторой переменной значение функции или сложного выражения (листинг 3.13, вторая строка) и затем вывести значение переменной в символьном виде.
Листинг 3.12. Численный и символьный вывод значения функции
Листинг 3.13. ЧислвйныЙ и символьный вывод
Как показывают приведенные примеры, преимущество символьных вычислений заключается в выдаче аналитического результата, который для математика часто является более ценным. Поэтому, исходя из специфики конкретных задач, решайте, стоит ли наряду с численными расчетами попытаться получить и символьное решение.
3.1.5. Вывод значений переменных и функций MathCAD
Чтобы вычислить в документе некоторое математическое выражение, которое может состоять из переменных, операторов и функций (встроенных и определенных пользователем):
В результате справа от введенного знака равенства появится вычисленное значение выражения (листинг 3.5, предпоследняя строка). Нельзя изменять содержимое выражения справа от знака равенства, поскольку оно есть результат работы вычислительного процессора Mathcad, совершенно скрытой от глаз пользователя. Подчас (когда выражение содержит функции, реализующие разные численные методы, часто в сложных комбинациях) алгоритмы расчета бывают очень затейливыми и занимают существенное время. О том, что некоторое выражение документа находится в стадии вычисления, свидетельствует обрамляющая его зеленая рамка и невозможность предпринять какое-либо действие с программой Mathcad.
Листинг 3.5. Вычисление выражения.
Заметьте, что, перед тем как вычислить значение математического выражения, Вы обязаны определить значение каждой входящей в него переменной (две первых строки листинга 3.5). Вычисляемое выражение может содержать любое количество переменных, операторов и функций. Вывод текущего значения той или иной переменной приведен в последней строке листинга 3.5, а значения функции — в листингах 3.6 и 3.7.
Листинг 3.6. Вывод значения функции.
Листинг 3.7. Вывод значения функции (продолжение листинга 3.6)
Листинг 3.8. К определению функций пользователя
Листинг 3.9. К определению функций пользователя (продолжение листинга 3.8)
Внимательнее относитесь к обязательному требованию совпадения количества аргументов при определении и выводе значения функций. Сравните, например, листинги 3.6 и 3.8, в которых, несмотря на одинаковое выражение в правой части определения функции f, создаются две существенно разные функции f (х, у) и f (х), соответственно
Вводя знак равенства для вычисления математических выражений в Math-cad, Вы фактически применяете оператор вычисления или численного вывода (numerical evaluation). Его можно ввести также нажатием кнопки со знаком равенства на одной из панелей инструментов: Calculator (Калькулятор) или Evaluation (Выражения) (см. рис. 3.1). Оператор численного вывода означает, что все вычисления проводятся с числами, а различные встроенные алгоритмы реализуются соответствующими численными методами.
Формат результата MathCAD
Управление представлением числа в десятичном представлении или представлении с порядком осуществляется при помощи следующих параметров:
Количество десятичных знаков левого сомножителя числа с порядком контролируется в некоторых форматах первым из трех перечисленных параметров.
В Mathcad имеется несколько типов форматов, в каждом из которых разрешается изменение различных параметров представления числа. Формат выбирается на вкладке Number Format (Формат числа) диалогового окна Result Format (Формат результата) (рис. 4.20).
Рис. 4.20. Выбор формата вывода числа
Основной (general) формат
Этот формат принят при выводе чисел по умолчанию. Можно управлять и количеством отображаемых десятичных знаков (поле Number of decimal places), и порядковым порогом (поле Exponential threshold). При превышении порога число отображается с порядком (как показано на рис. 4.20). Несколько примеров вывода одного и того же числа в общем формате показано в листинге 4.21. В левой колонке приведены числа с порядковым порогом, равным 3, и количеством десятичных знаков (сверху вниз) 3, 4, 5, соответственно. Для нижнего числа установлен флажок отображения незначащих нулей. В правой колонке сгруппированы числа с порядковым порогом от 1 до 4 (сверху вниз).
Листинг 4.21. Основной формат результата
Десятичный (decimal) формат
Числа отображаются только в десятичном представлении и никогда — в представлении с порядком.
Научный (scientific) формат
Числа отображаются только с порядком, причем количество десятичных знаков левого сомножителя, как и отображение незначащих нулей, определяется пользователем.
Инженерный (engineering) формат
Числа отображаются только с порядком, причем обязательно кратным 3; как и в научном формате, пользователю разрешается изменять количество десятичных знаков.
Дробный (fraction) формат
Этот формат сильно отличается от предыдущих, представляя число в виде дроби (рис. 4.21). Причем можно управлять как точностью представления числа с помощью поля level of accuracy (Уровень точности), так и задать модификацию этого формата — отображение числа в виде целой и дробной части (как показано на рис. 4.21 внизу слева) посредством установки флажка Use mixed numbers (Смешанные числа).
Вид одного и того же числа в различных форматах приведен в листинге 4.22. В первой строке показан десятичный формат, во второй строке — научный с тремя десятичными знаками, в третьей — инженерный также с тремя десятичными знаками. В последних двух строках представлен дробный формат: в предпоследней с уровнем точности 5, в последней — 10. К тому же, для выражения последней строки установлен флажок Use mixed numbers (Смешанные числа).
Рис. 4.21. Дробный формат
Листинг 4.22. Другие форматы результаа вычислений
200 тыс км/с в стекле и
3 млн. км/с в поверхностных слоях металлов, разную скорость в эфире (см. статью «Температура эфира и красные смещения»), разную скорость для разных частот (см. статью «О скорости ЭМ-волн»)
3. В релятивизме возможны манипуляции со временем (замедление), поэтому там нарушаются основополагающие для любой науки принцип причинности и принцип строгой логичности. В релятивизме при скорости света время останавливается (поэтому в нем абсурдно говорить о частоте фотона). В релятивизме возможны такие насилия над разумом, как утверждение о взаимном превышении возраста близнецов, движущихся с субсветовой скоростью, и прочие издевательства над логикой, присущие любой религии.
4. В гравитационном релятивизме (ОТО) вопреки наблюдаемым фактам утверждается об угловом отклонении ЭМ-волн в пустом пространстве под действием гравитации. Однако астрономам известно, что свет от затменных двойных звезд не подвержен такому отклонению, а те «подтверждающие теорию Эйнштейна факты», которые якобы наблюдались А. Эддингтоном в 1919 году в отношении Солнца, являются фальсификацией. Подробнее читайте в FAQ по эфирной физике.
ПРОСТЕЙШИЕ ВЫЧИСЛЕНИЯ И ОПЕРАЦИИ В MATHCAD
ПРОСТЕЙШИЕ ВЫЧИСЛЕНИЯ И ОПЕРАЦИИ В MATHCAD
Цель работы: научиться производить расчёты простейших арифметических и алгебраических выражений.
Порядок выполнения работы
I. Вычислить значения арифметических выражений 25+ 



Если при вводе выражения была допущена ошибка, выделите неправильный символ угловой рамкой (щелкните мышью справа внизу возле символа), удалите выделенный символ (нажмите клавишу ) и введите в помеченной позиции исправление.
Mathcad читает и выполняет введенные выражения слева направо и сверху вниз, поэтому следите, чтобы выражение для вычисления располагалось правее или ниже определенных для него значений переменных.
III. Определить функцию f(x) = 
IV. Построить график функции f
* При вводе с клавиатуры символа в рабочем документе отображается знак присваивания:=

Индивидуальные задания к лабораторной работе 1
I. Вычислить значения арифметических выражений:
| 1. |  | 11. |  |
| 2. |  | 12. |  |
| 3. | 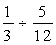 | 13. |  |
| 4. |  | 14. |  |
| 5. |  | 15. |  |
| 6. |  | 16. |  |
| 7. |  | 17. | 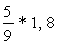 |
| 8. |  | 18. |  |
| 9. |  | 19. |  |
| 10. |  | 20. |  |
II. Вычислить значение выражения:
| 1. | 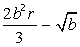 , при , при  | 11. |  , при , при 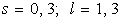 |
| 2. |  , при , при  | 12. |  , при , при  |
| 3. |  , при , при  | 13. |  , при , при  |
| 4. |  , при , при  | 14. |  , при , при  |
  5. 5. |  , при , при  | 15. | 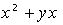 , при , при  |
| 6. |  , при , при  | 16. |  , при , при  |
| 7. |  , при , при  | 17. |  , при , при  |
| 8. |  , при , при  | 18. |  , при , при  |
| 9. | 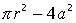 , при , при  | 19. |  , при , при  |
| 10. |  , при , при  | 20. |  , при , при  |
III. Определить функцию f(x), вычислить ее значение при x=2,9 и построить таблицу значений функции для x [2;12] с шагом 1. Построить график функции.
| 1. |  | 11. |  |
| 2. | 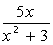 | 12. |  |
| 3. |  | 13. |  |
| 4. |  | 14. |  |
| 5. |  | 15. |  |
| 6. | 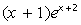 | 16. |  |
| 7. | 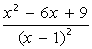 | 17. | 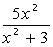 |
| 8. | 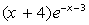 | 18. | 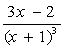 |
| 9. |  | 19. | 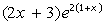 |
| 10. | 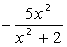 | 20. |  |

1. Что такое табулирование функции?
2. Каково предназначение математического пакета MathCad?
3. Приведите простейший пример вычислительной задачи.
Литература:
1.Информатика: Базовый курс. Учебник под редакцией С.В.Симановича.
3.Ю.Ю.Тарасевич Численные методы на MathCad. – Астраханский гос. Пед. Ун-т: Астрахань,2000.

Порядок выполнения работы
I. Упростить выражение
Ниже приведен фрагмент рабочего документа Mathcad с соответствующими вычислениями.
Большинство вычислений в Mathcad можно выполнить тремя способами выбором операции в меню, с помощью кнопочных панелей инструментов или обращением к соответствующим функциям.
Преобразование алгебраических выражений
В Mathcad можно выполнить следующие символьные преобразования алгебраических выражений:
simplify (упростить) выполнить арифметические операции, привести подобные, сократить дроби, использовать для упрощения основные тождества (формулы сокращенного умножения, тригонометрические тождества и т.п.);
expand (развернуть) раскрыть скобки, перемножить и привести подобные;
factor (разложить на множители) представить, если возможно, выражение в виде произведения простых сомножителей;
substitute (подставить) заменить в алгебраическом выражении букву или выражение другим выражением;
convert to partial fraction разложить рациональную дробь на простейшие дроби.
Если Mathcad не может выполнить требуемую операцию, то он выводит в качестве результата вычислений исходное выражение. Все приведенные вычисления выполнены в предположении, что в меню Math установлен автоматический режим вычислений и отключен режим оптимизации. Следует помнить, что Mathcad далеко не всегда преобразует выражение к самому простейшему виду.

Прежде чем вводить знак умножения и второй сомножитель, нажмите несколько раз клавишу (Пробел); нажимайте пробел до тех пор, пока весь первый сомножитель не будет заключен в выделяющую рамку. Затем введите знак умножения и второй сомножитель нажмите на клавиатуре клавиши в следующей последовательности:*
Рис. 31. Процесс упрощения выражения через меню Symbolics
Рис.32. Упрощение выражений с использованием операции Expand.
III. Разложить на множители выражение
Ниже приведен фрагмент рабочего документа Mathcad с соответствующими вычислениями.

Ниже приведен фрагмент рабочего документа Mathcad с соответствующими вычислениями.
Указание. Введите описанным выше способом выражение для преобразова-ний, выделите переменную х и щелкните по строке Convert to Partial Fraction в пункте Variable меню Symbolics.
V. Построить таблицу значений функции
f(x) = xsin 
Ниже приведен фрагмент рабочего документа Mathcad с соответствующими вычислениями.
Указание. Определите функцию f(x) = xsin 



VI. Построить график функции f(x) =xsin 

Указание. Определите функцию f(x), как в предыдущем примере, щелкните по свободному месту в рабочем документе правее и ниже определения функции f(x), затем щелкните по кнопке декартова графика 

На рисунках 33 и 34 приведен фрагмент рабочего документа Mathcad с соответствующими определениями, графиками и окнами диалога.
Указание. Определите функцию f(x) и постройте ее график, действуя, как в предыдущем примере. Для того чтобы найти корни уравнения абсциссы точек пересечения графика функции с осью у = 0, щелкните по строке Trace в пункте Graph меню Format. Затем щелкните по полю графиков и установите (стрелками клавиатуры или мышью) маркер (перекрещивающиеся пунктирные линии) в точке пересечения графика функции с осью абсцисс. В окне диалога отображаются координаты маркера: значение координаты х в окне и есть искомое приближенное значение корня.
Рис. 33. Определение координат на точки
  |  |
 | Рис. 34. Окна диалога настройки параметров декартова графика |
VIII. Решить символьно уравнение 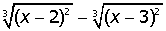
Символьное решение этого уравнения в Mathcad занимает одну строчку.
Указание. Щелкните по кнопке решения уравнений 

Порядок выполнения работы
Задание. Исследуйте и, если решение существует, найдите по формулам Крамера решение системы
Указание:
1. Установите режим автоматических вычислений и режим отображения результатов вычислений по горизонтали.
2. Присвойте переменной ORIGIN значение, равное 1.
3. Введите матрицу и столбец правых частей.
4. Вычислите определитель матрицы.
5. Вычислите определители матриц, полученных заменой соответствующего столбца столбцом правых частей.
Указание. Для вычисления определителей D1, D2, D3, D4 проще всего скопировать матрицу А в буфер обмена ( + или пункт Copy меню Edit), затем вставить в помеченной позиции матрицу из буфера обмена ( + или пункт Insert меню Edit) и затем заменить элементы соответствующего столбца элементами столбца правых частей.
6.Найдите по формулам Крамера решение системы.
Выполните индивидуальные задания приведенные ниже. Подготовьте отчет по лабораторной работе в виде экранного документа.
 |
Индивидуальные задания к лабораторной работе 3.
Исследуйте и, если решение существует, найдите по формулам Крамера решение системы Ах = B.
1. А = 
2. A = 
3. A = 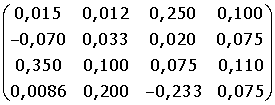
4. A = 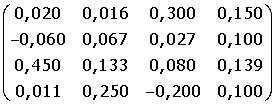
5. A= 
6. A = 
7. A = 

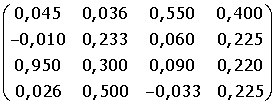
9. A = 
10. A = 
11. A= 
12. A = 
13. A = 

14. A = 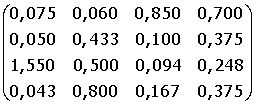
15. A = 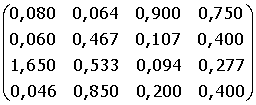


17. A = 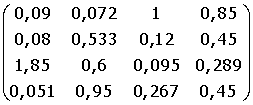
18. A = 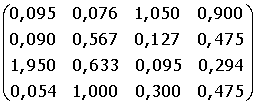
Содержание отчета
2. Решение всех задач с комментариями.
Контрольные вопросы
1. Назовите основные способы решения систем линейных уравнений.
2. Какие операторы позволяют осуществить решение систем нелинейных уравнений?
3. Для чего необходимо выполнять проверку решения уравнений?
5. Назовите порядок построения графика в декартовых системах координат.
6. Назовите порядок построения графика в полярной системе координат.
Литература:
1. Информатика: Базовый курс. Учебник под редакцией С.В.Симановича.
3. Ю.Ю.Тарасевич Численные методы на MathCad. – Астраханский гос. Пед. Ун-т: Астрахань,2000.
Лабораторная работа 4

Цель работы: Освоить работу с процессом символьных вычислений на примере вычисления интегралов, производных, сумм, пределов. Изучить работу с векторами и матрицами.
Задание:
1. По заданным координатам точек A, B, C, D найти координаты векторов a=AB и b=CD.
2. Вычислить скалярное и векторное произведения найденных векторов.
3. Найти следующие произведения векторов на заданную матрицу M: a*M и M*b.
4. Вычислить определитель матрицы M.
5. Для заданного ряда вычислить i-частичную сумму и исследовать сходимость ряда.
6. Вычислить сумму ряда.
7. Найти первообразную неопределенного интеграла и выполнить проверку, полученного результата.
8. Вычислить значения определенного интеграла.
Пример выполнения задания:
1. Для выполнения задания 1 используем известную формулу из курса линейной алгебры, которая гласит, что координаты вектора численно равны разности координат точек конца и начала вектора:

Для этого в MathCAD точки A, B, C и D набираются в следующем виде:
Для чего открываем панель инструментов «Математика» (View\Toolbars\Math) и нажимаем на ней кнопку «Матрицы» ([MMM])
Далее задаем параметр i, меняющийся от 0 до 2 (для чего на панели «Матрица» есть кнопка вида “m..n”).
Примечание. Отметим, что в пакете MathCAD нумерация компонент векторов и элементов матриц начинается с 0:

Для просмотра координат векторов достаточно набрать «a=» и «b=». В данной задаче
Рекомендация: предлагаем читателю самостоятельно вычислить в MathCAD длину полученных векторов.
2. Вычислим скалярное и векторное произведение полученных векторов.
Примечание. Обращаем внимание на то, что вычисление скалярного произведения в MathCAD осуществляется согласно правилу умножения матриц.
В связи с этим вектора следует задавать следующим образом:
Примечание. Верхний индекс Т у вектора а означает операцию транспонирования и является результатом работы кнопки M T на панели «Матрица».
Вычислим скалярное произведение:
Проверим результат, воспользовавшись определением скалярного произведения:
Примечание. Если вектор задан в строчку, то MathCAD воспринимает его не как вектор, а как матрицу с одной строкой и n столбцами. Для набора нижнего индекса можно нажимать на клавиатуре кнопку [.

В качестве примера продемонстрируем проверку антикоммутативности векторного произведения
3. Рассмотрим произведение матрицы на вектор. Матрица задается с помощью встроенных функций пользователя, а произведение ее на вектор в MathCAD имеет вид:
Умножение вектора на матрицу осуществляется следующим образом:
4. Вычисление определителя матрицы выполняется с помощью встроенной символьной операции 
5. Частичные суммы рядов вычисляются с помощью определенных символьных операций, представленных на рис. 1.
Результаты вычислений имеют вид:
Примечание. Из курса математического анализа известно, что частичные суммы в теории рядов представляют собой отправную точку в исследовании их сходимости. Средства MathCAD позволяют, используя фундаментальное определение сходимости числового ряда, рассмотреть этот вопрос для различных числовых рядов. Здесь в качестве примера мы рассматриваем заданный выше ряд.

В среде MathCAD для вычисления пределов используются встроенные символьные операции, представленные на рис. 1. Результаты вычислений выглядят следующим образом:
6. Ряд сходится, следовательно, можно вычислить его сумму:
7. Для вычисления неопределенных интегралов также используются встроенные символьные вычисления (см. рис. 1).
Примечание. Отметим, что в полученном результате отсутствует аддитивная постоянная.
Согласно основному свойству интегралов производная от первообразной должна быть равна подынтегральной функции. Часто это свойство используется в качестве проверки полученных первообразных.
Для вычисления производных снова используем встроенные символьные вычисления (см. рис. 1).
В нашем случае получаем:
8. Для вычисления определенного интеграла, используя символьные операции, получаем
Примечание. Возможности пакета позволяют с помощью указанных символьных операций проводить исследования сходимости несобственных интегралов и изучение поведения разрывных функций на заданном интервале.
В чем предлагаем читателю убедиться самостоятельно, рассмотрев следующие два примера:
1. 


2. Решение всех задач с комментариями.
Контрольные вопросы
1. Назовите способы выполнения символьных операций в MathCAD.
2. Что необходимо сделать с выражением перед применением символьных преобразований в командном режиме?
3. Перечислите символьные операции с выделенными выражениями.
4. Перечислите символьные операции с выделенными переменными.
5. Перечислите символьные операции с выделенными матрицами.
6. Перечислите символьные операции преобразования.
7. Какие параметры определяет стиль представления результатов вычислений и где он задается?
8. В каких случаях результат символьных преобразований помещается в буфер обмена?
9. Каким образом можно вычислить предел в MathCAD?
Литература:
1. Информатика: Базовый курс. Учебник под редакцией С.В.Симановича.
3. Ю.Ю.Тарасевич Численные методы на MathCad. – Астраханский гос. Пед. Ун-т: Астрахань,2000.