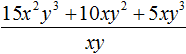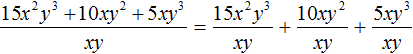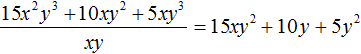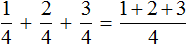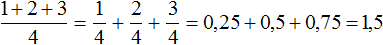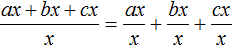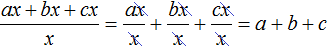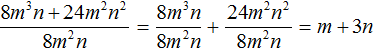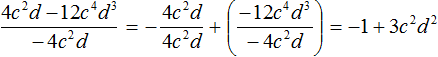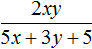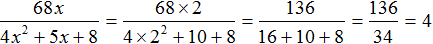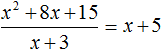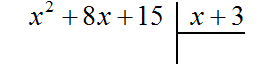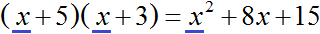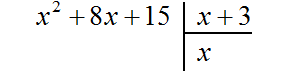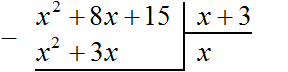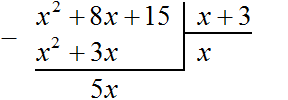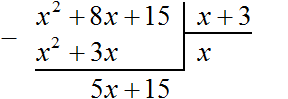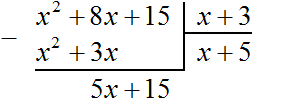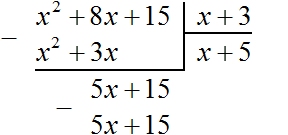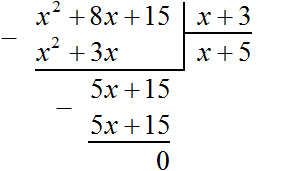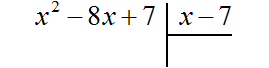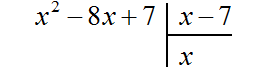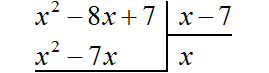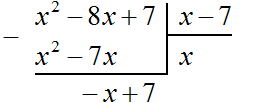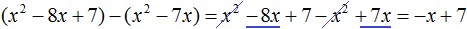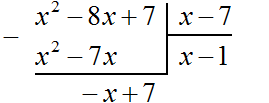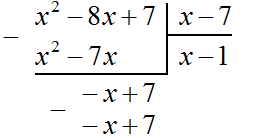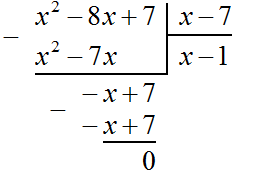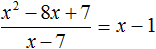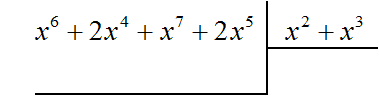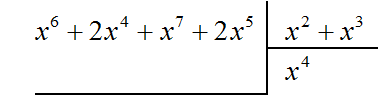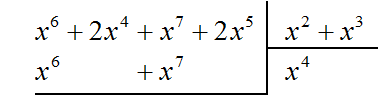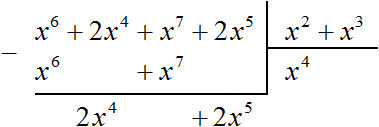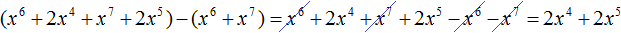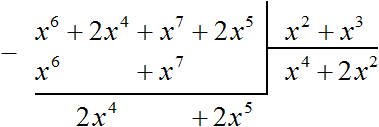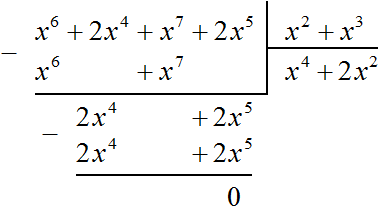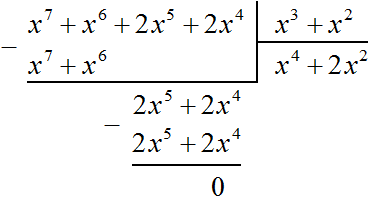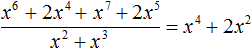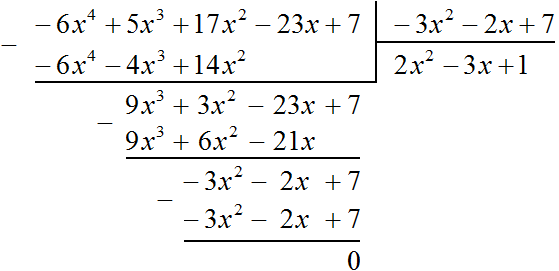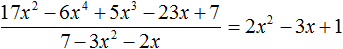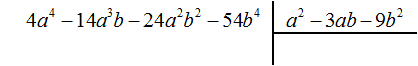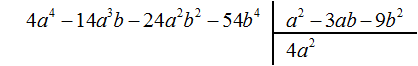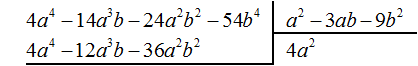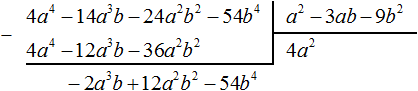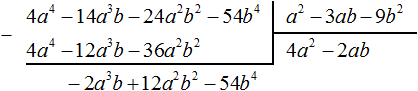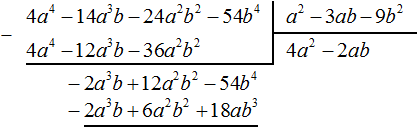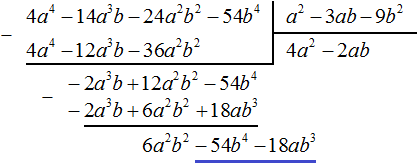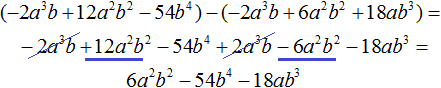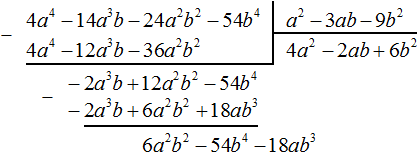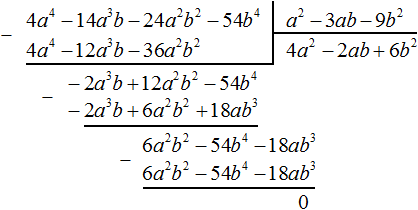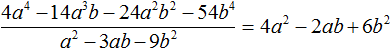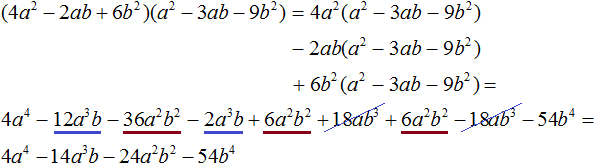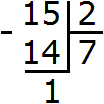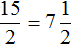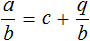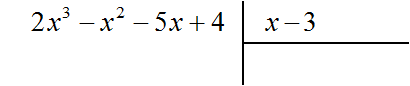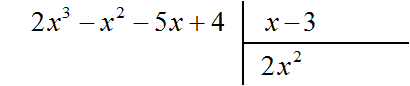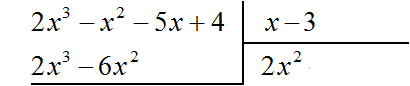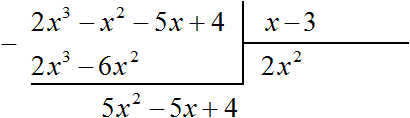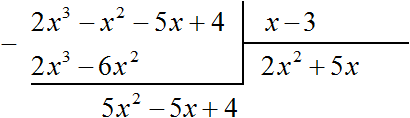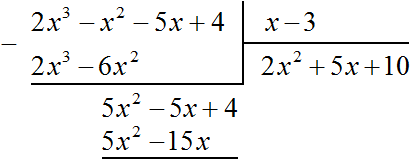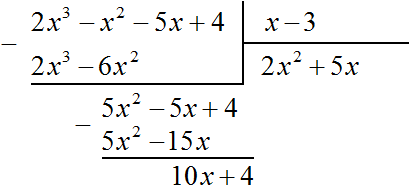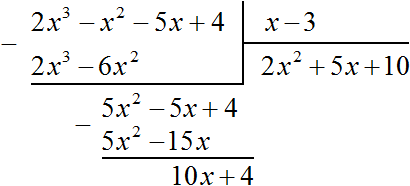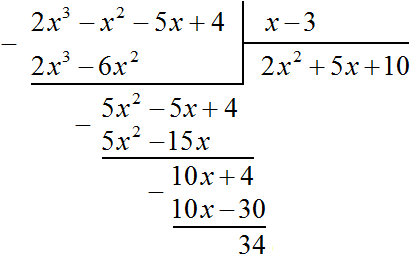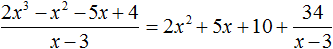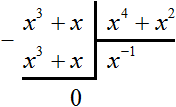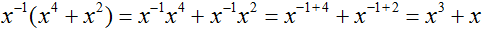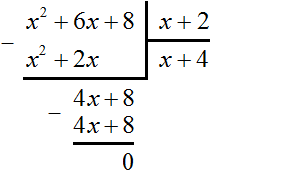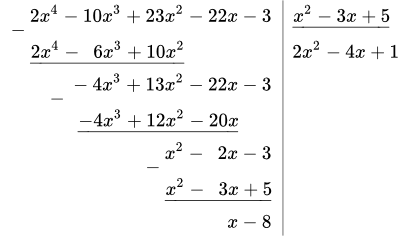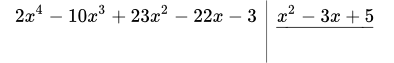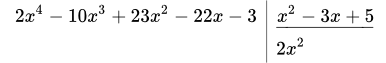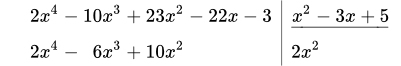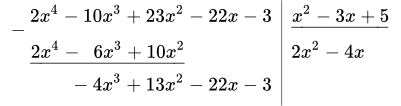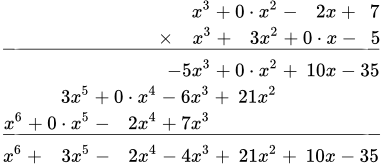Как выполнять деление уголком многочлена

Решение задач по математике онлайн

//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘

Калькулятор онлайн.
Деление многочлена на многочлен (двучлен) столбиком (уголком)

С помощью данной математической программы вы можете поделить многочлены столбиком.
Программа деления многочлена на многочлен не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс решения для того чтобы проконтролировать знания по математике и/или алгебре.

Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

Если вам нужно или упростить многочлен или умножить многочлены, то для этого у нас есть отдельная программа Упрощение (умножение) многочлена

Немного теории.

Деление многочлена на многочлен (двучлен) столбиком (уголком)

В алгебре деление многочленов столбиком (уголком) — алгоритм деления многочлена f(x) на многочлен (двучлен) g(x), степень которого меньше или равна степени многочлена f(x).

Алгоритм деления многочлена на многочлен представляет собой обобщенную форму деления чисел столбиком, легко реализуемую вручную.

Для любых многочленов \( f(x) \) и \( g(x) \), \( g(x) \neq 0 \), существуют единственные полиномы \( q(x) \) и \( r(x) \), такие что
$$ \frac = q(x)+\frac $$
причем \( r(x) \) имеет более низкую степень, чем \( g(x) \).

Целью алгоритма деления многочленов в столбик (уголком) является нахождение частного \( q(x) \) и остатка \( r(x) \) для заданных делимого \( f(x) \) и ненулевого делителя \( g(x) \)

Пример

Разделим один многочлен на другой многочлен (двучлен) столбиком (уголком):
$$ \frac $$

6. Конец алгоритма.
Таким образом, многочлен \( q(x)=x^2-9x-27 \) — частное деления многочленов, а \( r(x)=-123 \) — остаток от деления многочленов.

Результат деления многочленов можно записать в виде двух равенств:
\( x^3-12x^2-42 = (x-3)(x^2-9x-27)-123 \)
или
$$ \frac = x^2-9x-27 + \frac<-123> $$

Источник

Деление многочлена на многочлен «уголком»

Пример:
\(6x^2+6+x^3+11x\) записываем как \(x^3+6x^2+11x+6\)

1) Подбором найдите один из корней многочлена.

Для этого вместо \(x\) подставьте по очереди числа: \(±1,±2,±3,±4,±5\) и т.д. Число, которое сделает многочлен нулем и будет его корнем.

Матхак! Пробуйте сначала числа, на которые свободный член делиться нацело. В данном случае свободный член \(6\), поэтому в первую очередь нужно пробовать числа: \(±1,±2,±3\) и \(±6\).

а) Запишите многочлены как числа при делении столбиком:

б) Подберите такой одночлен, чтобы при умножении его на \(x\), получалось первое слагаемое исходного многочлена, то есть в нашем случае \(x^3\). Очевидно, что таким одночленом будет \(x^2\).

в) Умножьте этот одночлен на делитель и запишите результат под исходным многочленом. Таким образом, мы умножаем \(x^2\) на \(x+1\) и получаем \(x^3+x^2\).

г) Теперь точно так же, как в случае деления натуральных чисел, поставьте знак минус, проведите горизонтальную черту и сделайте вычитание.

д) Повторите шаги б) – г) только уже с новым многочленом:
— подберите такой одночлен, чтобы при умножении на \(x\) первое слагаемое было таким же, как в новом многочлене: в нашем примере этим одночленом будет \(5x\).
— умножьте этот одночлен на делитель: умножив \(5x\) на \(x+1\) получим \(5x^2+5x\).
— вычтите получившиеся многочлены:

е) И вновь повторяем шаги б) – г) до тех пор, пока после вычитания не останется ноль.

3) Запишите новый вид многочлена, представив его как произведение делителя и частного.
\(x^3+6x^2+11x+6=(x+1)(x^2+5x+6)\)

Матхак! Если есть сомнения в правильности разложения, можно проверить его раскрытием скобок – в результате должен получиться исходный многочлен.
Проверим наш случай: \((x+1)(x^2+5x+6)=x^3+5x^2+6x+x^2+5x+6=x^3+6x^2+11x+6\).
Получен исходный многочлен, значит, поделили правильно.

Матхак! Если в результате деления у вас в остатке получился не ноль, значит, скорее всего, в решении есть ошибка.

Давайте теперь решим пример с применением изученного материала.

Пример: Решите неравенство \(x^4-3x^3+6x-4≥0\).

Найдем один из корней многочлена слева. Проверим \(1\).

Поделим многочлен \(x^4-3x^3+6x-4\) на \((x-1)\) уголком. Однако замечаем, что у нас нет слагаемого с квадратом. Чтоб нам было удобнее решать, запишем вместо него выражение \(0·x^2\) (ведь его значение равно нулю, а значит оно ничего не меняет в исходном многочлене).

Запишем новый вид нашего неравенства.

Теперь выносим общую скобку \((x-2)\) за скобку.

Источник

Деление многочленов

Продолжаем изучать многочлены. В данном уроке мы научимся их делить.

Деление многочлена на одночлен

Чтобы разделить многочлен на одночлен, нужно разделить на этот одночлен каждый член многочлена, затем сложить полученные частные.

Теперь делим каждый член многочлена 15x 2 y 3 + 10xy 2 + 5xy 3 на одночлен xy. Получающиеся частные будем складывать:

Получили привычное для нас деление одночленов. Выполним это деление:

При делении одного числа на другое, частное должно быть таким, чтобы при его перемножении с делителем, получалось делимое. Это правило сохраняется и при делении многочлена на одночлен.

Деление многочлена на одночлен очень похоже на сложение дробей с одинаковыми знаменателями. Мы помним, что для сложения дробей с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить без изменений.

Например, чтобы сложить дроби , и нужно записать следующее выражение:

Если мы вычислим выражение 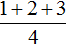, то получим дробь , значение которой равно 1,5.

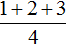
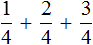
При этом выражение мы можем вернуть в исходное состояние , и вычислить по отдельности каждую дробь, затем сложить полученные частные. Результат по прежнему будет равен 1,5

Вычисление каждой дроби даст в результате многочлен a + b + c

Пример 2. Разделить многочлен 8m 3 n + 24m 2 n 2 на одночлен 8m 2 n

Пример 3. Разделить многочлен 4c 2 d − 12c 4 d 3 на одночлен −4c 2 d

Деление одночлена на многочлен

Не существует тождественного преобразования, позволяющего разделить одночлен на многочлен.

Но в учебниках можно встретить задания на нахождение значения выражения при заданных значениях переменных. В исходных выражениях таких заданий бывает выполнено деление одночлена на многочлен. В этом случае никаких преобразований выполнять не нужно. Достаточно подставить значения переменных в исходное выражение и вычислить получившееся числовое выражение.

Выражение 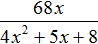представляет собой деление одночлена на многочлен. В данном случае мы не сможем выполнить какие-либо преобразования. Единственное, что мы сможем сделать — это подставить число 2 в исходное выражение вместо переменной x и найти значение выражения:

Деление многочлена на многочлен

Если произведение разделить на множитель, то получится множимое. Это правило распространяется не только для чисел, но и для многочленов.

Деление многочлена на многочлен выполняется уголком. Отличие будет в том, что при делении многочленов не нужно определять первое неполное делимое, как в случае деления обычных чисел.

Результатом деления должен быть новый многочлен. Члены этого многочлена будут появляться один за другим в процессе деления.

Сейчас наша задача найти первый член нового многочлена. Как это сделать?

Этот же принцип нахождения первого члена будет выполняться и при решении других задач на деление многочленов.

Итак, чтобы найти первый член нового многочлена, нужно первый член делимого разделить на первый член делителя.

Если первый член делимого (в нашем случае это x 2 ) разделить на первый член делителя (это x), получится x. То есть первым членом нового многочлена является x. Записываем его под правым углом:

Теперь, как и при делении обычных чисел, сносим следующий член делимого. Следующий член это 15. Сносить его нужно вместе со своим знаком:

На этом деление завершено.

Пример 2. Разделить многочлен x 2 − 8x + 7 на многочлен x − 7

Записываем уголком данное деление:

Следует быть внимательным при вычитании отрицательных членов. Часто на этом этапе допускаются ошибки. Если на первых порах вычитание в столбик даётся тяжело, то можно использовать обычное вычитание многочленов в строку, которое мы изучили ранее. Для этого нужно отдельно выписать делимое и вычесть из него многочлен, который под ним располагается. Преимущество этого метода заключается в том, что следующие члены делимого сносить не нужно — они автоматически перейдут в новое делимое. Давайте воспользуемся этим методом:

Деление завершено. Таким образом, частное от деления многочлена x 2 − 8x + 7 на многочлен x − 7 равно x − 1

Пример 3. Разделить многочлен x 6 + 2x 4 + x 7 + 2x 5 на многочлен x 2 + x 3

Найдём первый член частного. Разделим первый член делимого на первый член делителя, получим x 4

Вычитание многочлена 2x 4 + 2x 5 из многочлена 2x 4 + 2x 5 дало в результате 0, поэтому деление успешно завершилось.

В промежуточных вычислениях члены нового делимого располагались друг от друга, образуя большие расстояния. Это было по причине того, что при умножении частного на делитель, результаты были записаны так, чтобы подобные члены располагались друг под другом.

Эти расстояния между членами нового делимого образуются тогда, когда члены исходных многочленов расположены беспорядочно. Поэтому перед делением желательно упорядочить члены исходных многочленов в порядке убывания степеней. Тогда решение примет более аккуратный и понятный вид.

Тогда деление уголком многочлена x 6 + 2x 4 + x 7 + 2x 5 на многочлен x 2 + x 3 примет следующий вид:

Деление завершено. Таким образом, частное от деления многочлена x 6 + 2x 4 + x 7 + 2x 5 на многочлен x 2 + x 3 равно x 4 + 2x 2

При перемножении многочленов члены исходных многочленов тоже желательно упорядочивать в порядке убывания степеней. Тогда члены полученного многочлена тоже будут упорядочены в порядке убывания степеней.

Перепишем умножение (x 4 + 2x 2 )(x 2 + x 3 ) упорядочив члены многочленов в порядке убывания степеней.

Пример 4. Разделить многочлен 17x 2 − 6x 4 + 5x 3 − 23x + 7 на многочлен 7 − 3x 2 − 2x

Упорядочим члены исходных многочленов в порядке убывания степеней и выполним уголком данное деление:

Пример 5. Разделить многочлен 4a 4 − 14a 3 b − 24a 2 b 2 − 54b 4 на многочлен a 2 − 3ab − 9b 2

Умножим 4a 2 на делитель a 2 − 3ab − 9b 2 и полученный результат запишем под делимым:

Вычтем из делимого полученный многочлен 4a 4 − 12a 3 b − 36a 2 b 2

Умножим −2ab на делитель a 2 − 3ab − 9b 2 и полученный результат запишем под делимым −2a 3 b + 12a 2 b 2 − 54b 4

Этот же результат можно получить, если выполнить вычитание многочленов в строку с помощью скобок:

Деление многочлена на многочлен с остатком

Как и при делении обычных чисел, при делении многочлена на многочлен может образоваться остаток от деления.

Для начала вспомним деление обычных чисел с остатком. Например, разделим уголком 15 на 2. С остатком это деление будет выполнено так:

То есть при делении 15 на 2 получается 7 целых и 1 в остатке. Ответ записывается следующим образом:

Рациональное число читается как семь целых плюс одна вторая. Знак «плюс» по традиции не записывают. Но если при делении многочлена на многочлен образуется остаток, то этот плюс записывать нужно.

Например, разделим многочлен 2x 3 − x 2 − 5x + 4 на многочлен x − 3

Умножим 2x 2 на делитель x − 3 и полученный результат запишем под делимым:

Вычтем из делимого полученный многочлен 2x 3 − 6x 2

Умножим 5x на делитель x − 3 и полученный результат запишем под делимым 5x 2 − 5x + 4

Вычтем из многочлена 5x 2 − 5x + 4 многочлен 5x 2 − 15x

Поэтому при делении многочлена 2x 3 − 2x 2 − 5x + 4 на многочлен x − 3 получается 2x 2 + 5x + 10 и 34 в остатке. Ответ записывается таким же образом, как и при делении обычных чисел. Сначала записывается целая часть (она располагается под правым углом) плюс остаток, разделенный на делитель:

Когда деление многочленов невозможно

Деление многочлена на многочлен невозможно в случае, если степень делимого окажется меньше степени делителя.

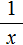
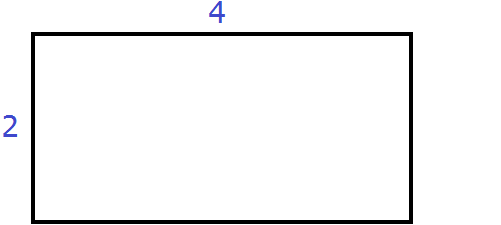
Но при делении многочлена на многочлен должен получаться именно многочлен, а частное x − 1 многочленом не является. Ведь многочлен состоит из одночленов, а одночлен в свою очередь это произведение чисел, переменных и степеней. Выражение x − 1 это дробь , которая не является произведением.

Пусть имеется прямоугольник со сторонами 4 и 2

Площадь этого прямоугольника будет равна 4 × 2 = 8 кв.ед.

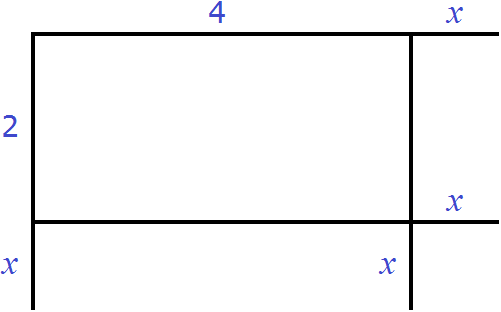
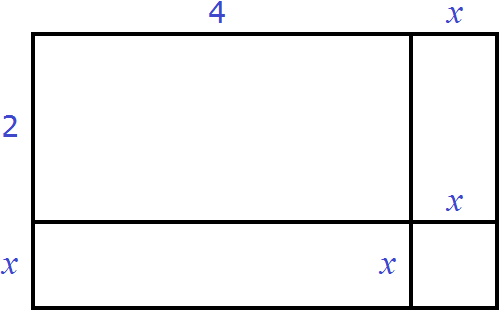
Увеличим длину и ширину этого прямоугольника на x

Достроим отсутствующие стороны:

Источник

Деление и умножение многочленов уголком и столбиком

Теорема

Доказательство

Деление многочленов

Уравнение (4) показывает, что любую неправильную дробь многочленов можно упростить, представив ее в виде суммы целой части и правильной дроби.

Деление многочленов уголком

Поэтому к многочленам можно применить правило деления уголком (иногда его называют делением в столбик), применяемое к делению чисел. Единственное отличие заключается в том, что, при делении многочленов, не нужно переводить числа больше девяти в старшие разряды. Рассмотрим процесс деления многочленов уголком на конкретных примерах.

Пример деления многочленов уголком

Выделить целую часть дроби и найти остаток от деления:
.

Приведем подробное описание процесса деления. Исходные многочлены записываем в левый и правый столбики. Под многочленом знаменателя, в правом столбике, проводим горизонтальную черту (уголок). Ниже этой черты, под уголком, будет целая часть дроби.

1.2 Умножаем 2 x 2 на x 2 – 3 x + 5 :
. Результат записываем в левый столбик:

1.3 Берем разность многочленов в левом столбике:

.

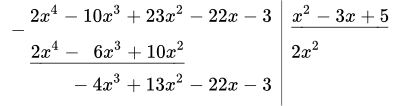
Итак, мы получили промежуточный результат:
.

Дробь в правой части неправильная, поскольку степень многочлена в числителе ( 3 ) больше или равна степени многочлена в знаменателе ( 2 ). Повторяем вычисления. Только теперь числитель дроби находится в последней строке левого столбика.
2.1 Разделим старший член числителя на старший член знаменателя: ;

2.2 Умножаем на знаменатель: ;

2.3 И вычитаем из последней строки левого столбика: ;

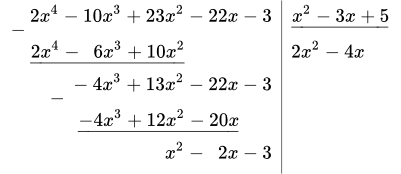
Промежуточный результат:
.

;
2 x 2 – 4 x + 1 – это целая часть;
x – 8 – остаток от деления.

Пример 2

Выделить целую часть дроби и найти остаток от деления:
.

Выполняем те же действия, что и в предыдущем примере:

Здесь остаток от деления равен нулю:
.

Умножение многочленов столбиком

Также можно умножать многочлены столбиком, аналогично умножению целых чисел. Рассмотрим конкретные примеры.

Пример умножения многочленов столбиком

Найти произведение многочленов:
.

Умножаем многочлены столбиком.

1 Записываем исходные многочлены друг под другом в столбик и проводим черту.

2.1 Умножаем младший член второго многочлена на первый многочлен:
.
Результат записываем в столбик.

3 После того, как все члены второго многочлена умножили на первый, проводим черту и складываем члены с одинаковыми степенями x :
;
;
;
.

Заметим, что можно было записывать только коэффициенты, а степени переменной x можно было опустить. Тогда умножение столбиком многочленов будет выглядеть так:

Пример 2

Найти произведение многочленов столбиком:
.

При умножении многочленов столбиком важно записывать одинаковые степени переменной x друг под другом. Если некоторые степени x пропущены, то их следует записывать явно, умножив на нуль, либо оставлять пробелы.

В этом примере некоторые степени пропущены. Поэтому запишем их явно, умноженными на нуль:
.
Умножаем многочлены столбиком.

1 Записываем исходные многочлены друг под другом в столбик и проводим черту.

2.1 Умножаем младший член второго многочлена на первый многочлен:
.
Результат записываем в столбик.

2.2 Следующий член второго многочлена равен нулю. Поэтому его произведение на первый многочлен также равно нулю. Нулевую строку можно не записывать.

3 После того, как все члены второго многочлена умножили на первый, проводим черту и складываем члены с одинаковыми степенями x :
.

Источник