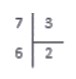
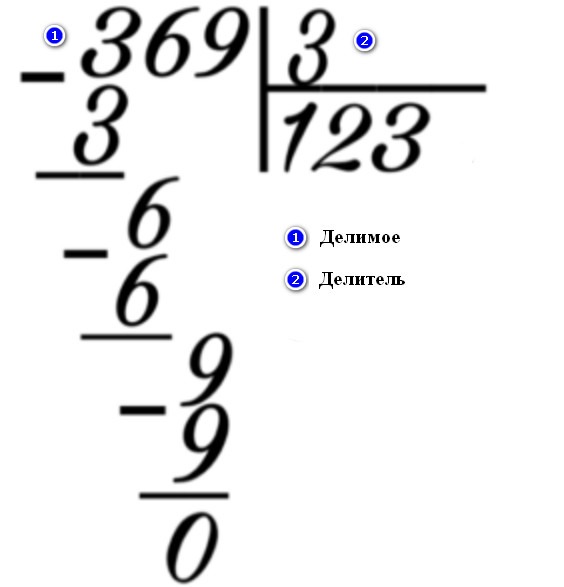
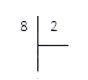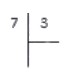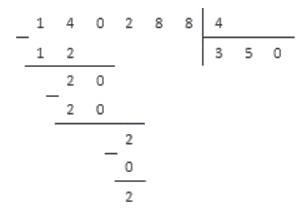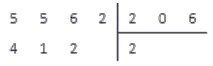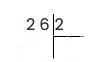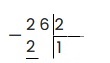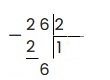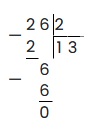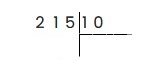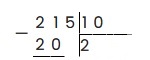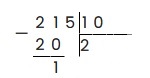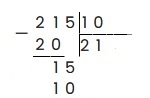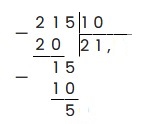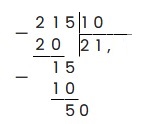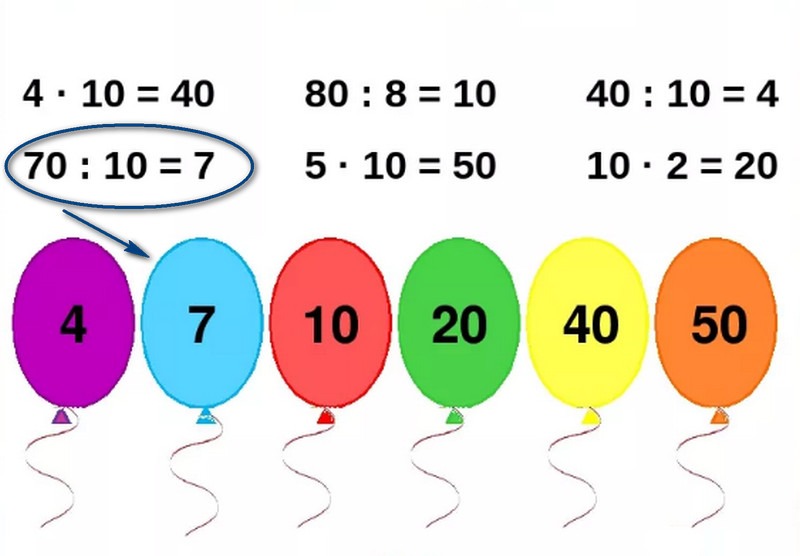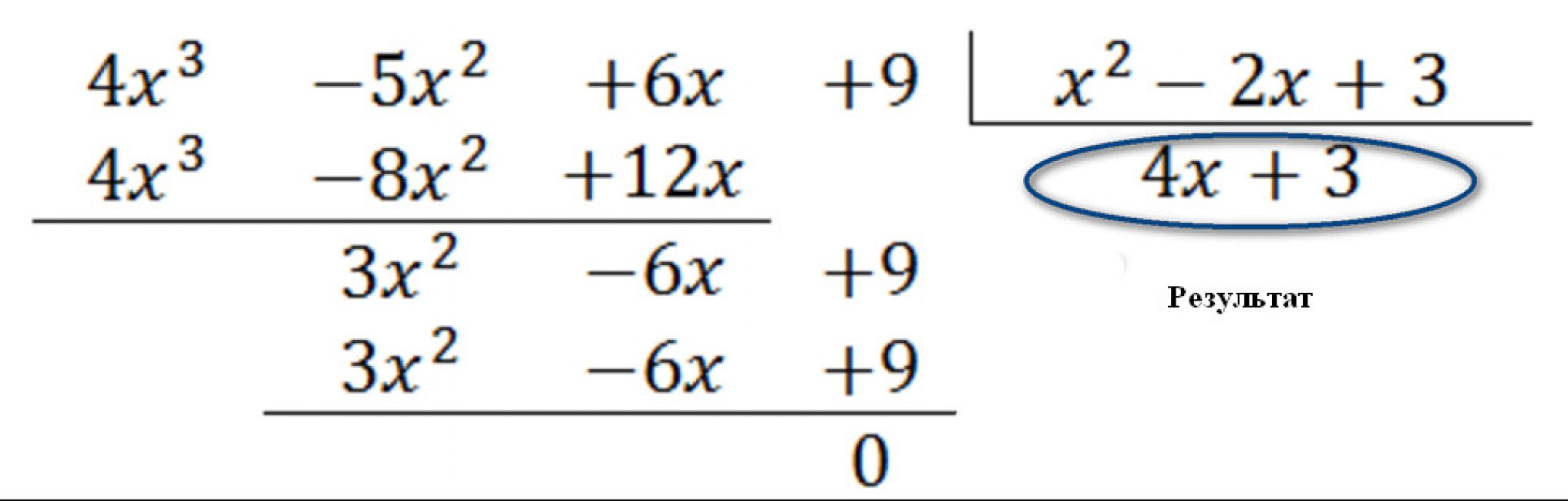Как выглядит знак деления столбиком
Деление в столбик
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Как правильно делить в столбик
Делить столбиком проще, чем высчитывать в уме. Этот способ наглядный, помогает держать во внимании каждый шаг и запомнить алгоритм, который впоследствии будет срабатывать автоматически.
Рассмотрим пример деления трехзначного числа на однозначное 322 : 7. Для начала определимся с терминами:
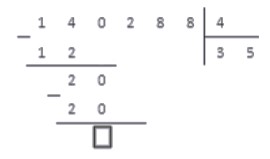
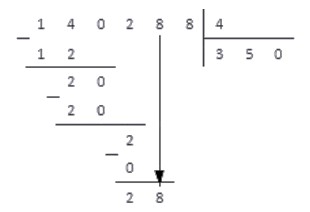
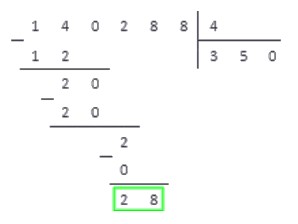
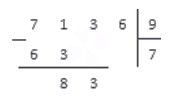
Шаг 1. Слева размещаем делимое 322, справа делитель 7, между ставим уголок, а частное посчитаем и запишем под делителем.
Шаг 2. Смотрим на делимое слева направо и находим ту часть, которая больше делителя. 3, 32 или 322? Нам подходит 32. Теперь нужно определить сколько раз наш делитель 7 содержится в числе 32. Похоже, что четыре раза.
Проверяем: 4 × 7 = 28, а 28
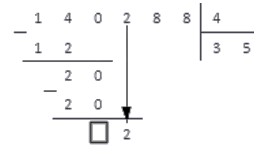
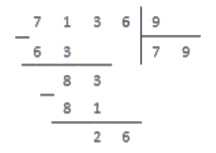
Шаг 3. Остаток равен 4. Для продолжения решения его нужно увеличить. Мы сделаем это за счет следующей цифры делимого. Приписываем к четверке оставшуюся двойку и продолжаем размышлять.
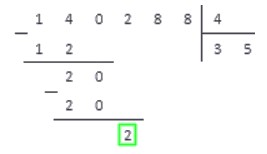
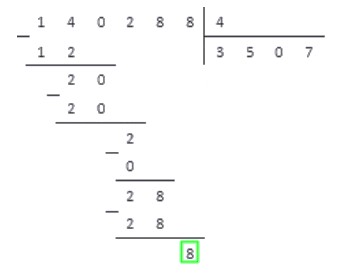
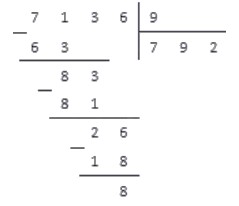
Шаг 4. Сколько раз делитель 7 содержится в числе 42? Кажется, шесть раз. Проверяем: 7 × 6 = 42, 42 = 42 — все верно. Записываем полученное число к четверке справа — это вторая цифра частного. Делаем вычитание в столбик 42 из 42, в остатке получаем 0. Значит, числа разделились нацело.
Мы закончили решать пример и в результате получили целое число 46.
Как выглядит деление в столбик с остатком
Это такое же деление, только в результате получается неровное число, как получилось в примере выше.
Примеры на деление в столбик
Давайте закрепим знания на практике. Для этого разделите столбиком примеры ниже, а после проверьте полученные цифры — чур, не подглядывать!
Деление натуральных чисел столбиком: правило, примеры
Однозначные натуральные числа легко делить в уме. Но как делить многозначные числа? Если в числе уже более двух разрядов, устный счет может занять много времени, да и вероятность ошибки при операциях с многоразрядными числами возростает.
Запись чисел при делении столбиком
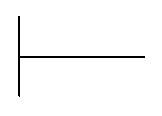
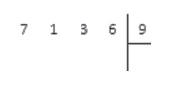
Удобнее всего вести записи на бумаге в клетку, так как при расчетах разлиновка не даст вам запутаться в разрядах. Сначала делимое и делитель записываются слева направо в одну строчку, а затем разделяются специальным знаком деления в столбик, который имеет вид:
Промежуточные вычисление будем записывать под делимым, а результат запишется под делителем. В общем случае схема деления столбиком выглядит так:
Следует помнить, что для вычислений понадобится свободное место на странице. Причем, чем больше разница в разрядах делимого и делителя, тем больше будет вычислений.
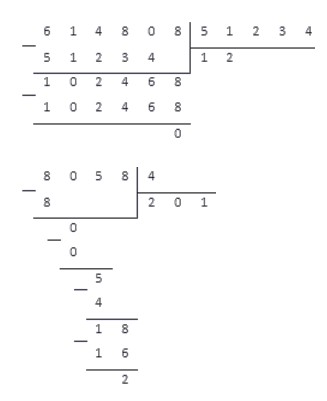
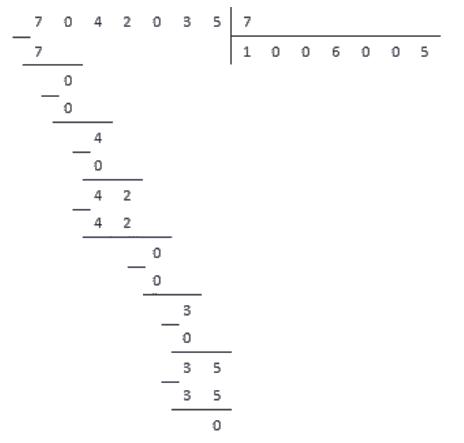
Например, для деления чисел 614 808 и 51 234 понадобится меньше места, чем для деления числа 8 058 на 4. Несмотря на то, что во втором случае числа меньше, разница в числе их разрядов больше, и вычисления будут более громоздкими. Проиллюстрируем это:
Деление столбиком на однозначное число
Итак, сначала запишем делимое и делитель согласно методу деления в столбик.
Иначе, когда получается число, большее чем делимое, под делителем записываем число, вычисленное на предпоследнем шаге.На место неполного частного записываем то число, на которое умножался делитель на предпоследнем шаге.
Вернемся к примеру.
2 · 0 = 0 ; 2 · 1 = 2 ; 2 · 2 = 4 ; 2 · 3 = 6 ; 2 · 4 = 8
3 · 0 = 0 7 ; 3 · 1 = 3 7 ; 3 · 2 = 6 7 ; 3 · 3 = 9 > 7
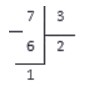
В завершение операции вычитаем 6 из 7 и получаем:
Теперь, после рассмотрения элементарых примеров, перейдем к делению многозначных натуральных чисел на однозначные.
Алгоритм деления столбиком
В соответствии с алгоритмом имеем:
Принимаем это число за рабочее и снова выполняем пункты алгоритма.
4 · 0 = 0 2 ; 4 · 1 = 4 > 2
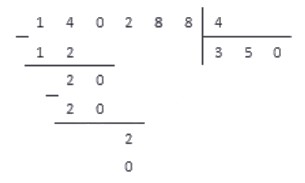
3. Выполняем операцию вычитания и под чертой записываем результат.
Проделав все по правилам, получаем результат:
Приведем другие примеры деления чисел в столбик и примеры записи решений.
Пример 1. Деление натуральных чисел в столбик
После второго, третьего и четвертого шага алгоритма запись примет вид:
Последний проход, и поучаем результат:
При решении практических примеров в иделе вообще не использовать пояснения в виде словесных комментариев.
Пример 2. Деление натуральных чисел в столбик
Деление многозначных натуральных чисел столбиком
Рассмотрим применение алгоритма деления многозначных чисел на примере.
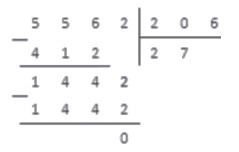
Пример 3. Деление натуральных чисел в столбик
206 · 0 = 0 556 ; 206 · 1 = 206 556 ; 206 · 2 = 412 556 ; 206 · 3 = 618 > 556
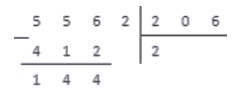
Выполняем вычитание столбиком
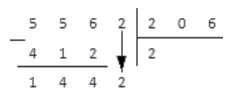
206 · 5 = 1030 1442 ; 206 · 6 = 1236 1442 ; 206 · 7 = 1442
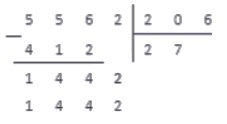
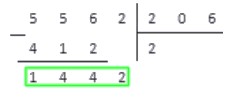
Выполняем вычитание в столбик, и понимаем, что на этом операция деления окончена: в делителе более нет цифр, чтобы записать их правее от результата вычитания.
В завершение данной темы приведем еще один пример деления многозначных чисел в столбик, уже без пояснений.
Пример 5. Деление натуральных чисел в столбик
Деление в столбик.
Столбиком можно проводить как деление натуральных чисел без остатка, так и деление натуральных чисел с остатком.
Правила записи при делении столбиком.
Начнем с изучения правил записи делимого, делителя, всех промежуточных выкладок и результатов при делении натуральных чисел столбиком. Сразу скажем, что письменно выполнять деление столбиком удобнее всего на бумаге с клетчатой разлиновкой – так меньше шансов сбиться с нужной строки и столбца.
Сначала в одной строке слева направо записываются делимое и делитель, после чего между записанными числами изображается символ вида 
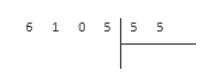
Например, если делимым является число 6105, а делителем 55, то их правильная запись при делении в столбик будет такой:
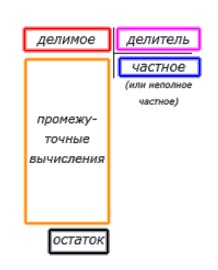
Посмотрите на следующую схему, иллюстрирующую места для записи делимого, делителя, частного, остатка и промежуточных вычислений при делении столбиком:
Из приведенной схемы видно, что искомое частное (или неполное частное при делении с остатком) будет записано ниже делителя под горизонтальной чертой. А промежуточные вычисления будут вестись ниже делимого, и нужно заранее позаботиться о наличии места на странице. При этом следует руководствоваться правилом: чем больше разница в количестве знаков в записях делимого и делителя, тем больше потребуется места.
Деление столбиком натурального числа на однозначное натуральное число, алгоритм деления столбиком.
Как делить в столбик лучше всего объяснить на примере. Вычислить :
Для начала запишем делимое и делитель в столбик. Выглядеть это будет так:
Их частное (результат) будем записывать под делителем. У нас это цифра 8.
1. Определяем неполное частное. Сначала мы смотрим на первую слева цифру в записи делимого. Если число, определяемое этой цифрой, больше делителя, то в следующем пункте нам предстоит работать с этим числом. Если же это число меньше, чем делитель, то нам нужно добавить к рассмотрению следующую слева цифру в записи делимого, и работать дальше с числом, определяемым двумя рассматриваемыми цифрами. Для удобства выделим в нашей записи число, с которым мы будем работать.
2. Берём 5. Цифра 5 меньше 8, значит нужно взять еще одну цифру из делимого. 51 больше 8. Значит. это неполное частное. Ставим точку в частном (под уголком делителя).
После 51 стоит только одно цифра 2. Значит и добавляем в результат ещё одну точку.
3. Теперь, вспоминая таблицу умножения на 8, находим ближайшее к 51 произведение → 6 х 8 = 48 → записываем цифру 6 в частное:
Записываем 48 под 51 (если умножить 6 из частного на 8 из делителя, получим 48).
4. Между 51 и 48 слева поставим «-» (минус). Вычтем по правилам вычитания в столбик 48 и под чертой запишем результат.
Однако, если результатом вычитания является нуль, то его не нужно записывать (если только вычитание в этом пункте не является самым последним действием, полностью завершающим процесс деления столбиком).
В остатке получилось 3. Сравним остаток с делителем. 3 меньше 8.
Внимание! Если остаток получился больше делителя, значит мы ошиблись в расчете и есть произведение более близкое, чем то, которое взяли мы.
5. Теперь под горизонтальной чертой справа от находящихся там цифр (или справа от места, где мы не стали записывать нуль) записываем цифру, расположенную в том же столбце в записи делимого. Если же в записи делимого в этом столбце нет цифр, то деление столбиком на этом заканчивается.
Число 32 больше 8. И опять по таблице умножения на 8, найдем ближайшее произведение → 8 x 4 = 32:
В остатке получился ноль. Значит, числа разделились нацело (без остатка). Если после последнего вычитания получается ноль, а цифр больше не осталось, то это остаток. Его дописываем к частному в скобках (например, 64(2) ).
Деление столбиком многозначных натуральных чисел.
Деление на натуральное многозначное число производится аналогично. При этом, в первое «промежуточное» делимое включается столько старших разрядов, чтобы оно получилось больше делителя.
Значит, 1976 : 26 = 76.
Если на каком-то шаге деления «промежуточное» делимое оказалось меньше делителя, то в частном записывается 0, а число из данного разряда переводится в следующий, более младший разряд.
Деление с десятичной дробью в частном.
Десятичные дроби онлайн. Перевод десятичных дробей в обычные и обычных дробей в десятичные.
Если натуральное число не делится нацело на однозначное натуральное число, можно продолжить поразрядное деление и получить в частном десятичную дробь.
Например, 64 разделим на 5.
Таким образом, если при делении натурального числа на натуральное однозначное или многозначное число получается остаток, то можно поставить в частном запятую, остаток перевести в единицы следующего, меньшего разряда и продолжать деление.
Деление в столбик
Сегодня мы рассмотрим вопрос, касающийся деления в столбик. Познакомимся с алгоритмом и закрепим материал на конкретных примерах.
Алгоритм деления в столбик
Делить столбиком гораздо проще, чем считать в уме. Для этого необходимо воспользоваться простым алгоритмом:
Примеры
Рассмотрим несколько примеров на закрепление алгоритма деления в столбик.
Пример 1: Разделить 26 на 2.
Слева записываем делимое, справа делитель, рисуем уголок.
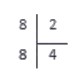
Делимое у нас — 26, делитель — 2. Наименьшее число, которое можно взять из делимого и разделить на 2, будет двойка. 2 делим на 2, получаем 1. 2 умножить на 1 получится 2. Записываем это:
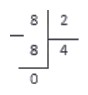
2 — 2 = 0, ноль писать не обязательно, поэтому исходя из алгоритма скидываем следующую цифру из делимого — 6
6 делим на 2 получаем 3, записываем в частное. 3 умножаем на 2 получаем 6. 6 — 6 = 0
Пример 2: Разделить 215 на 10.
Аналогично предыдущему примеру записываем условие уголком:
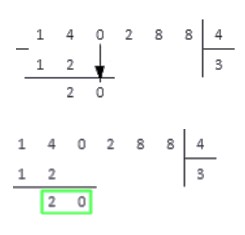
Наименьшее число, которое можно выделить из 215 и разделить на 10 — это 21. 21 делим на 10, и записываем в частное целую часть — 2. 2 умножаем на 10 — получаем 20:
21 — 20 = 1, записываем в остаток:
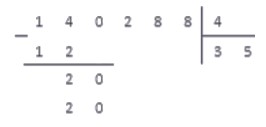
Сбрасываем из делимого оставшуюся цифру — 5, получаем 15. Аналогично делим 15 на 10 и получаем целую часть 1. 1 умножаем на 10, получаем 10, записываем:
15 — 10 = 5, записываем в остаток. 5 нацело на 10 не делится. Возвращаемся к 7 пункту алгоритма и ставим запятую в частном:
А, к остатку добавляем 0:
Теперь 50 мы легко можем разделить на 10 без остатка:
Деление многозначных чисел столбиком на двузначное, трехзначное число в 3,4 классе: как объяснить ребенку + ТОП-10 примеров
Дети во 2-3 классе осваивают новое математическое действие – деление. Школьнику непросто вникнуть в суть данного математического действия, поэтому ему необходима помощь родителей. Родителям нужно понимать, как именно преподносить ребенку новую информацию. ТОП-10 примеров расскажут родителям о том, как нужно учить детей делению чисел столбиком.
Содержание этой статьи:
Обучение делению в столбик в форме игры
Дети устают в школе, они устают от учебников. Поэтому родителям нужно отказаться от учебников. Подавайте информацию в форме увлекательной игры.
Можно поставить задачи таким образом:
Обучение в игровой форме может помочь ребенку быстрее понять весь процесс деления чисел. Он сможет усвоить, что наибольшее число делится на наименьшее или наоборот. То есть, наибольшее число – это конфеты, а наименьшее – участники. В столбике 1 числом будет количество конфет, а 2 – количество участников.
Обучение делению в столбик при помощи таблицы умножения
Ученики до 5 класса смогут разобраться в делении быстрее, при условии того, что они хорошо знают умножениz.
Родителям необходимо разъяснить, что деление имеет сходство с таблицей умножения. Только действия противоположны. Для наглядности нужно привести пример:
Можно воспользоваться таблицей умножения для наглядности деления, если ребенок хорошо ее усвоил.
Обучение делению в столбик в тетради
Начинать обучение нужно тогда, когда ученик понял материал о делении на практике, с помощью игры и таблицы умножения.
Нужно начинать делить таким образом, применяя простые примеры. Так, деление 105 на 5.
Объяснять математическое действие нужно подробно:
Родителям нужно объяснить, что это деление не имеет остатка.
Начать деление можно с цифр 6,8,9, затем переходить к 22, 44, 66, а после к 232, 342, 345, и так далее.
Еще один пример деления
Обучение делению с остатком
Когда ребенок усвоит материал о делении, можно усложнять задачу. Деление с остатком – это следующая ступень обучения. Объяснять нужно на доступных примерах:
Деление с остатком
Простые примеры для ребенка
На этом же примере можно продолжить:
Данный пример может показаться ребенку сложным. Поэтому нужно много раз делить значения, у которых будет остаток.
Обучение делению с помощью игр
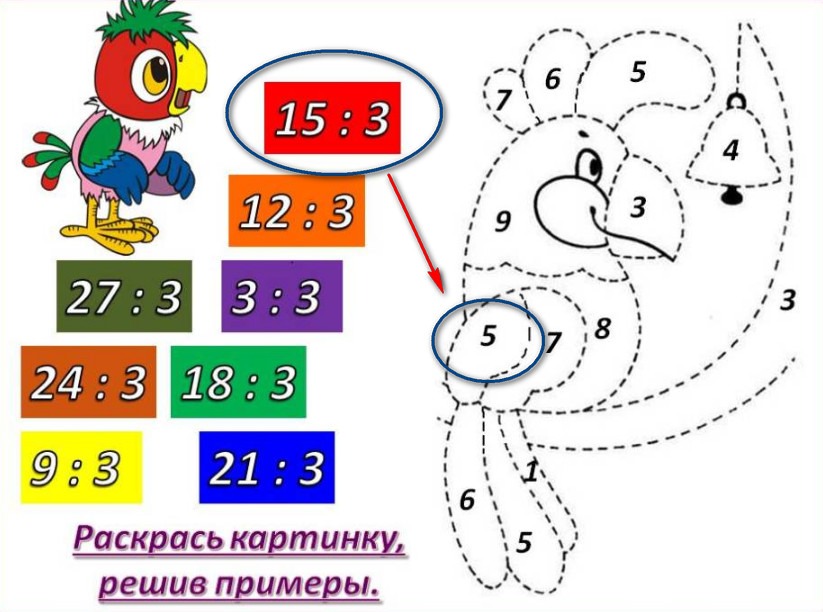
Родители могут использовать игры на деление для обучения школьника. Можно дать ребенку раскраски, в которых нужно определить цвет карандаша путем деления. Нужно выбирать раскраски с легкими примерами, чтобы ребенок мог решить примеры в уме.
Картинка будет поделена на части, в которых будут результаты деления. А цвета, которые нужно использовать, будут примерами. Например, красный цвет помечен примером: 15 разделить на 3. Получится 5. Нужно найти часть картинки под этим номером и раскрасить ее. Математические раскраски увлекают детей. Поэтому родителям стоит попробовать данный способ обучения.
Веселый способ изучить деление чисел
Обучение делению столбиком наименьшего числа на наибольшее
Деление данным методом предполагает, что частное будет начинаться с 0, а после него будет стоять запятая.
Чтобы ученик корректно усвоил полученную информацию, ему необходимо привести такого плана пример:
Обучение делению столбиком десятичных дробей с запятой
Деление десятичных дробей может запутать ребенка из-за постановки запятой.
Деление десятичных дробей
Чтобы ребенок сориентировался в этом математическом действие, ему необходимо разложить информацию «по полочкам»:
Обучение делению чисел столбиком с нолями
Деление чисел с нолями идентично обычному делению. Родителям нужно объяснить ребенку основные нюансы:
Чтобы лучше усваивать материал, можно решить простой пример деления:
Предложите ребенку легкие примеры такого типа:
Далее можно переходить к сложным примерам. Но только после того, как ребенок усвоит результат.
ВИДЕО: Почему нельзя делить на ноль
Почему нельзя делить на 0
Правило школьной математики
Обучение делению столбиком в уме
Родители могут помочь ребенку научиться делить в уме. Это может пригодиться им не только в школе, но и в дальнейшей жизни.
В уме дети считают тоже столбиком. Это удобно и знакомо. У детей развито воображение, поэтому они смогут быстро освоить технику. Приступать к обучению деления столбиком в уме нужно тогда, когда ребенок без труда справляется с делением в тетради. Обучение:
Ребенок не сразу может освоить эту технику деления. Все зависит от родителей. Их задача заключается в помощи ребенку без давления.
ВИДЕО: Как научиться делить в уме
Тренажер быстрого деления в уме
Как научиться быстро и просто делить цифры в уме
Обучение делению многочленов
В 5-6 классе у детей появляется новое сложное математической действие. Деление многочленов.
Детям нужно рассказать тонкости деления данного формата:
Рекомендации для легкого обучения ребенка
Чтобы ребенок быстро осваивал новый математический материал, его необходимо заранее подготовить. Важно научить трехлетнего ребенка понятиям «целое» и «часть». Ребенка важно научить восприятию целого, как неразделимого и частей целого, как самостоятельного объекта.
Также важно пробудить интерес к предмету у ребенка. Этому способствуют аналоги математических игр в процессе игры. Наблюдение за природой тоже можно преобразовать в увлекательную математику.
Родителям нужно тренировать наблюдательность детей. Это ключ к пониманию математики и других предметов.
ВИДЕО: Деление в столбик
Деление в столбик
Как научиться ребенку делить числа в столбик
Родители – это главные помощники детей. Главная их задача – научить ребенка делению, но без применения жестких методов. На обучение может уйти не одна неделя, поэтому нужно готовиться и запасаться терпением. Теперь у родителей есть ТОП-10 примеров обучения. При этом затронуты разные возрастные категории. Если вы не согласны с рейтингом статьи, то просто поставьте свои оценки и аргументируйте их в комментариях. Ваше мнение очень важно для наших читателей. Спасибо!