Как перевести запятую в математике
Перенос запятой в десятичной дроби
Чтобы увеличить десятичную дробь в 10, 100, 1000 и т. д. раз, то есть умножить на 10, 100, 1000 и т. д., нужно в записи дроби перенести запятую вправо на 1, 2, 3 и т. д. цифры, приписав при необходимости нули справа.
1) Увеличив дробь 63,29 в 10 раз, получим дробь 632,9 так как:
Таким образом, увеличение дроби в 10 раз привело к переносу запятой на 1 цифру вправо.
2) Перенеся запятую в дроби 63,29 на 2 цифры вправо, получим число 6329, в 100 раз большее данной дроби 63,29:
3) Если учесть, что 63,29 = 63,2900, то, перенеся запятую в дроби 63,29 на 4 цифры вправо, получим число 632 900, в 10 000 раз большее первоначальной дроби.
Таким образом, перенося запятую в записи дроби на 1, 2 и т. д. цифры вправо, мы увеличиваем эту дробь соответственно в 10, 100 и т. д. раз.
Чтобы уменьшить десятичную дробь в 10, 100, 1000 и т. д. раз, нужно в записи дроби перенести запятую влево соответственно на 1, 2, 3 и т. д. цифры, приписав при необходимости нули слева.
1) Дробь 6,329 в 10 раз меньше дроби 63,29. Первая дробь получена из второй переносом запятой влево на 1 цифру.
2) Если в данной дроби 63,29 перенести запятую на 2 цифры влево, то получим дробь 0,6329, которая в 100 раз меньше данной.
Таким образом, перенося запятую в записи десятичной дроби на 1, 2 и т. д. цифры влево, мы уменьшаем эту дробь соответственно в 10, 100 и т. д. раз.
Десятичные дроби
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие десятичной дроби
Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.
Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которое можно представить число. Есть два формата записи:
В обыкновенной дроби над чертой принято писать делимое, которое становится числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление.
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. По сути, десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.
Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.
Свойства десятичных дробей
Главное свойство десятичной дроби звучит так: если к десятичной дроби справа приписать один или несколько нулей — ее величина не изменится. Это значит, что если в вашей дроби куча нулей — их можно просто отбросить. Например:
Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:
Обучение на курсах по математике — отличный способ закрепить полученные знания на практике и подтянуть сложные темы.
Как записать десятичную дробь
Давайте разберем на примерах, как записывается десятичная дробь. Небольшая напоминалка: сначала пишем целую часть, ставим запятую и после записываем числитель дробной части.
Пример 1. Перевести обыкновенную дробь 16/10 в десятичную.
Пример 2. Перевести 37/1000 в десятичную дробь.
Ответ: 37/1000 = 0,037.
Как читать десятичную дробь
Чтобы учитель вас правильно понял, важно читать десятичные дроби грамотно. Сначала произносим целую часть с добавлением слова «целых», а потом дробную с обозначением разряда — он зависит от количества цифр после запятой:
| Сколько цифр после запятой? | Читается, как |
|---|---|
| одна цифра — десятых; | 1,3 — одна целая, три десятых; |
| две цифры — сотых | 2,22 — две целых, двадцать две сотых; |
| три цифры — тысячных; | 23,885 — двадцать три целых, восемьсот восемьдесят пять тысячных; |
| четыре цифры — десятитысячных; | 0,5712 — ноль целых пять тысяч семьсот двенадцать десятитысячных; |
| и т.д. |
Сохраняй наглядную картинку, чтобы быстрее запомнить.
Преобразование десятичных дробей
Чтобы ни одна задача не смутила вас своей формулировкой, важно знать, как преобразовывать десятичные дроби в другие виды. Сейчас научимся!
Как перевести десятичную дробь в проценты
Уже в пятом классе задачки по математике намекают, что дроби как-то связаны с процентами. И это правда: процент — это одна сотая часть от любого числа, обозначают его значком %.
Чтобы узнать, как перевести проценты в дробь, нужно убрать знак % и разделить наше число на 100, как в примере выше.
А чтобы перевести десятичную дробь в проценты — умножаем дробь на 100 и добавляем знак %. Давайте на примере:
Выразить дробь в процентах просто: сначала превратим её в десятичную дробь, а потом применим предыдущее правило.
2/5 = 0,4
0,4 · 100% = 40%
8/25 = 0,32
0,32 · 100% = 32%
Чтобы разрезать торт на равные кусочки и не обижать гостей, нужно всего-то запомнить соотношения частей и целого. Наглядная табличка — наш друг-помощник:
Преобразование десятичных дробей
Десятичная дробь — это число с остатком, где остаток стоит после целой части и разделяется запятой.
Смешанная дробь — это тоже число с остатком, но остаток записывают в виде простой дроби (с черточкой).
Чтобы переводить десятичные дроби в смешанные, не нужно запоминать особые алгоритмы. Достаточно понимать определения и правильно читать заданную дробь — этим школьники и занимаются в 5 классе. А теперь давайте потренируемся!
Пример 1. Перевести 5,4 в смешанное число.
Пример 2. Перевести 4,005 в смешанное число.
Ответ: 4,005 = 4 1/200.
Пример 3. Перевести 5,60 в смешанное число.
Как перевести десятичную дробь в обыкновенную
Не будем придумывать велосипед и рассмотрим самый простой способ превращения десятичной дроби в обыкновенную. Вот, как это сделать:
Не забывайте про минус в ответе, если пример был про отрицательное число. Очень обидная ошибка!
Действия с десятичными дробями
С десятичными дробями можно производить те же действия, что и с любыми другими числами. Рассмотрим самые распространенные на простых примерах.
Как разделить десятичную дробь на натуральное число
Пример 2. Разделить 183,06 на 45.
Ответ: 183,06 : 45 = 4,068.
Как разделить десятичную дробь на обыкновенную
Чтобы разделить десятичную дробь на обыкновенную или смешанную, нужно представить десятичную дробь в виде обыкновенной, а смешанное число записать, как неправильную дробь.
Пример 1. Разделить 0,25 на 3/4.
Пример 2. Разделить 2,55 на 1 1/3.
Ответ: 2,55 : 1 1/3 = 1 73/80.
Как умножить десятичную дробь на обыкновенную
Чтобы умножить десятичную дробь на обыкновенную или смешанную, используют два правила за 6 класс. При первом приводим десятичную дробь к виду обыкновенной и потом умножаем на нужное число. Во втором случае приводим обыкновенную или смешанную дробь в десятичную и потом умножаем.
Пример 1. Умножить 2/5 на 0,8.
Пример 2. Умножить 0,28 на 6 1/4.
Ответ: 0,28 ∗ 6 1/4 = 0,8.
Правило умножения десятичных дробей на натуральные числа
Умножение десятичных дробей — общие принципы
Десятичная дробь — форма записи обыкновенной дроби, у которой знаменатель равен 10, 100, 1000 и т.д.
Числа со знаменателями 10, 100, 1000 и т.д. записывают без знаменателя. Сначала пишут целую часть, а потом числитель дробной части. Целую часть отделяют от дробной части запятой.
Например, вместо 5 7 10 пишут 5,7 (читают: «5 целых 7 десятых»).
Вместо 3 17 100 пишут 3,17 (читают: «3 целых 17 сотых»).
Десятичные дроби перемножают как целые числа, на запятые внимания не обращают. В результате отделяют запятой столько цифр справа, сколько их стоит после запятой во всех множителях вместе.
Задания подобного плана выполняют по следующему алгоритму:
В двух множителях три цифры после запятой. Нужно отделить три цифры справа в результате и поставить запятую.
Умножение десятичной дроби на обыкновенную дробь или смешанное число
Для того, чтобы умножить десятичную дробь на обыкновенную дробь, необходимо:
Для того, чтобы умножить десятичную дробь на смешанное число, необходимо:
Умножение десятичной дроби на натуральное число
Произведение десятичной дроби и натурального числа — сумма слагаемых, каждое из которых равно этой дроби, а количество слагаемых определяется натуральным числом.
Выражение представляют в виде суммы, в которой слагаемое 0,25 повторяется четыре раза:
Для того, чтобы умножить десятичную дробь на натуральное число, необходимо:
Алгоритм, как ставить запятую, правила переноса
Для того, чтобы в результате умножения правильно поставить запятую, надо:
При умножении десятичной дроби на 10, 100, 1000 и т. д. запятую в десятичной дроби переносят вправо на столько цифр, сколько нулей стоит в множителе после единицы.
Если количество цифр в десятичной дроби после запятой меньше количества нулей после единицы, то нужно:
При умножении десятичной дроби на 0,1; 0,01; 0,001 и т. д. переносят запятую влево на столько цифр, сколько нулей стоит перед единицей в множителе. Нуль целых также учитываем.
Примеры решения задач
Для объяснения решения действуем по алгоритму:
6 5 × 3 4 = 6 × 3 5 × 4 :
Чтобы умножить десятичную дробь на смешанное число:
Решаем пример по схеме:
Запятую в десятичной дроби переносим вправо на две цифры, так как в множителе после единицы стоит два нуля.
Запятую переносим влево на четыре цифры, так как в множителе перед единицей стоит четыре нуля.
Чтобы решить уравнение, нужно найти его корни или доказать, что корней нет.
Для закрепления навыков умножения десятичных дробей используют математические тренажеры.
Как перевести дробь в десятичную и наоборот
Что такое дробь: понятие
Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которой можно представить число. Есть два формата записи:
В обыкновенной дроби над чертой принято писать делимое, которое становится числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление.
Дроби бывают двух видов:
Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 3/7 и 31/45.
Неправильной — ту, у которой числитель больше знаменателя или равен ему. Например, 21/4. Такое число является смешанным и читается, как «пять целых одна четвертая», а записывается — 5 1\4.
Что такое десятичная дробь
Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. По сути, десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.
Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.
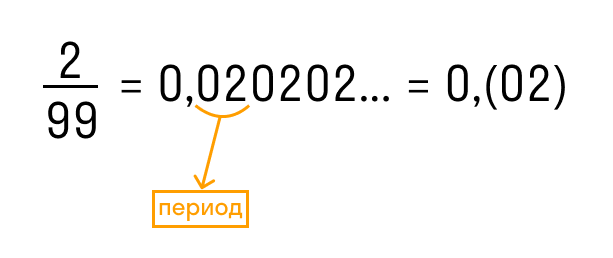
В краткой записи периодической дроби повторяющиеся цифры пишут в скобках и называют периодом дроби. Например, вместо 1,555… записывают 1,(5) и читают «одна целая и пять в периоде».
Обучение на курсах математики в Skysmart поможет улучшить оценки в школе и подготовиться к выпускным экзаменам!
Свойства десятичных дробей
Главное свойство десятичной дроби звучит так: если к десятичной дроби справа приписать один или несколько нулей — ее величина не изменится. Это значит, что если в вашей дроби куча нулей — их можно просто отбросить. Например:
Обыкновенная и десятичная дробь — давние друзья. Вот как они связаны:
Как перевести обычную дробь в десятичную
Прежде чем узнать, как от обычной записи перейти к десятичной, вспомним различия двух видов дробей и сформулируем важное правило.
Обыкновенную дробь можно перевести в конечную десятичную дробь только при условии, что её знаменатель можно разложить на простые множители 2 и 5 любое количество раз. Например:
Дробь 11/40 можно преобразовать в конечную десятичную, потому что знаменатель раскладывается на множители 2 и 5.
Дробь 17/60 нельзя преобразовать в конечную десятичную дробь, потому что в её знаменателе кроме множителей 2 и 5, есть 3.
А теперь перейдем к самому главному вопросу: рассмотрим несколько алгоритмов перевода обыкновенной дроби в десятичную.
Способ 1. Превращаем знаменатель в 10, 100 или 1000
Чтобы превратить дробь в десятичную, нужно числитель и знаменатель умножить на одно и то же число так, чтобы в знаменателе получилось 10, 100, 1000 и т.д. Но прежде, чем приступать к вычислениям, нужно проверить, можно ли вообще превратить данную дробь в десятичную.
Для примера возьмем дробь 3/20. Ее можно привести в конечную десятичную, потому что её знаменатель раскладывается на множители 2 и 5.
Мы можем получить в нижней части 100: достаточно умножить 20 на 5. Про верхнюю часть тоже не забываем: получаем 15.
Теперь запишем числитель отдельно. Отсчитываем справа столько же знаков, сколько нулей стоит в знаменателе, и ставим запятую. В нашем примере в знаменателе 100 (у него два нуля), значит ставим запятую после отсчета двух знаков и получаем 0,15. Преобразование готово.
Способ 2. Делим числитель на знаменатель
Чтобы перевести обыкновенную дробь в десятичную, достаточно разделить ее верхнюю часть на нижнюю. Проще всего это сделать, конечно же, на калькуляторе — но на контрольных им пользоваться не разрешают, поэтому учимся по-другому.
Для примера возьмем дробь 78/100. Убедимся, что дробь можно привести в конечную десятичную.
Делим столбиком числитель на знаменатель — преобразование готово:
Если при делении уголком стало ясно, что процесс не заканчивается и после запятой выстраиваются повторяющиеся цифры — эту дробь нельзя перевести в конечную десятичную. Ответ можно записать в виде периодической дроби — для этого нужно записать повторяющееся число в скобки, вот так: 1/3 = 0,3333.. = 0,(3).
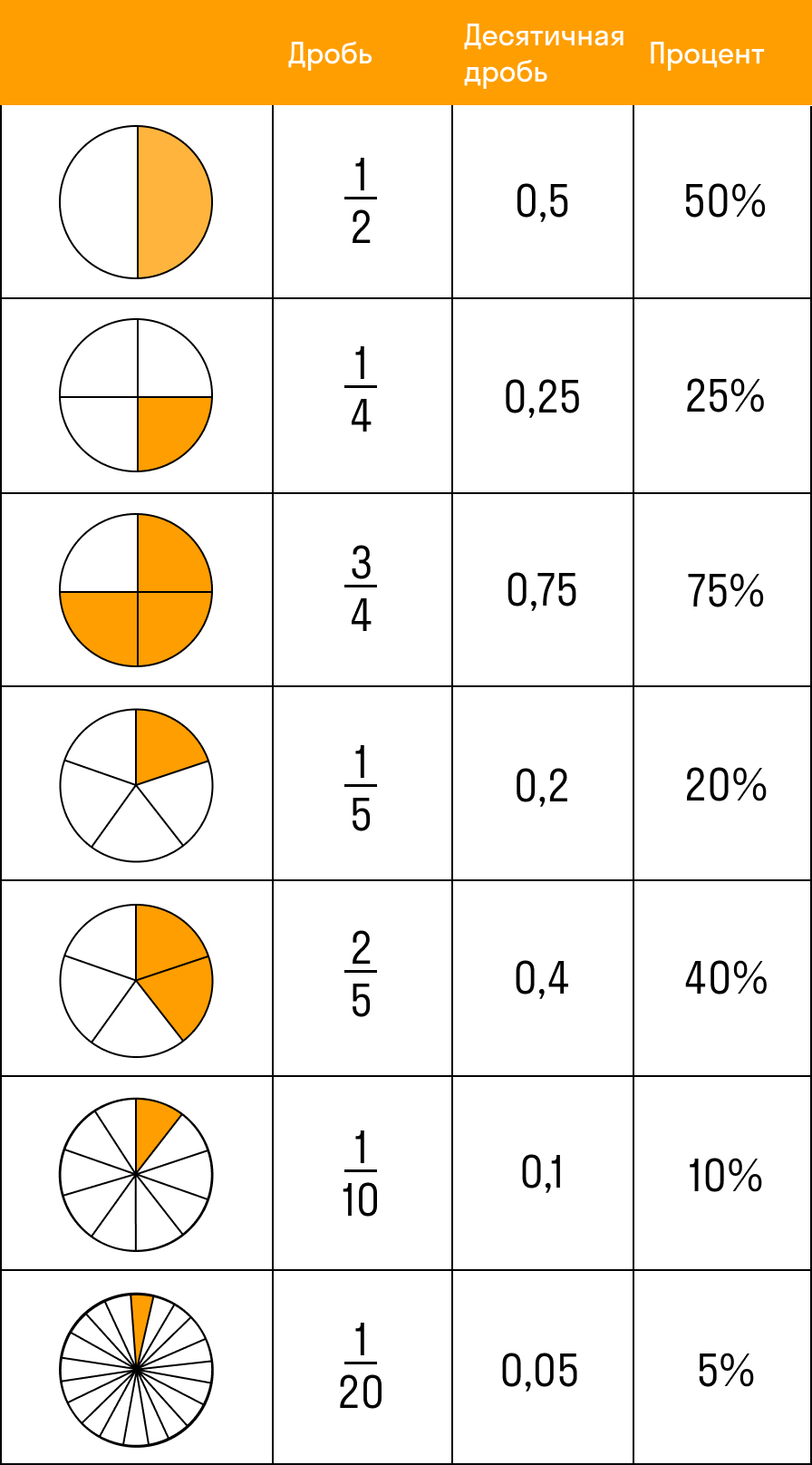
Для удобства мы собрали табличку дробей со знаменателями, которые чаще всего встречаются в заданиях по математике. Скачайте ее на гаджет или распечатайте и храните в учебнике как закладку:
Как перевести десятичную дробь в обыкновенную
Не будем придумывать велосипед. По сути, алгоритм превращения десятичной дроби в обыкновенную противоположен тем, что мы разобрали в предыдущей части. Вот, как это выглядит в обратную сторону:
Не забывайте про минус в ответе, если пример был про отрицательное число. Очень обидная ошибка!





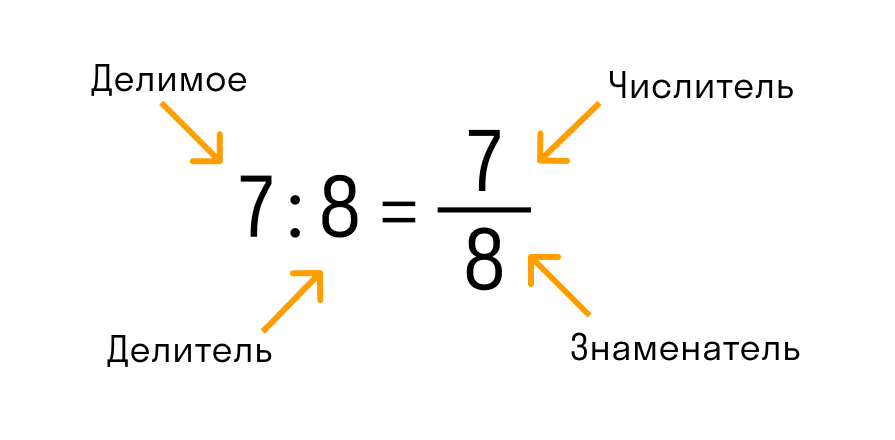
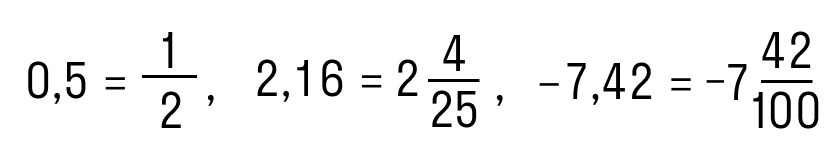
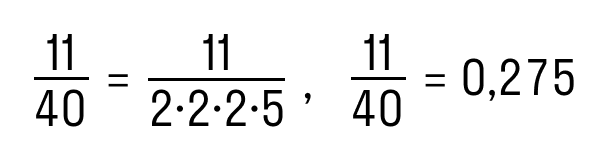
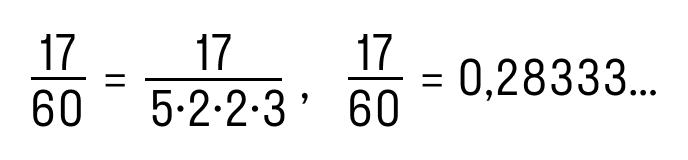
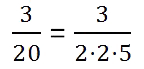
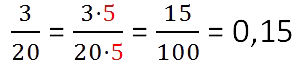
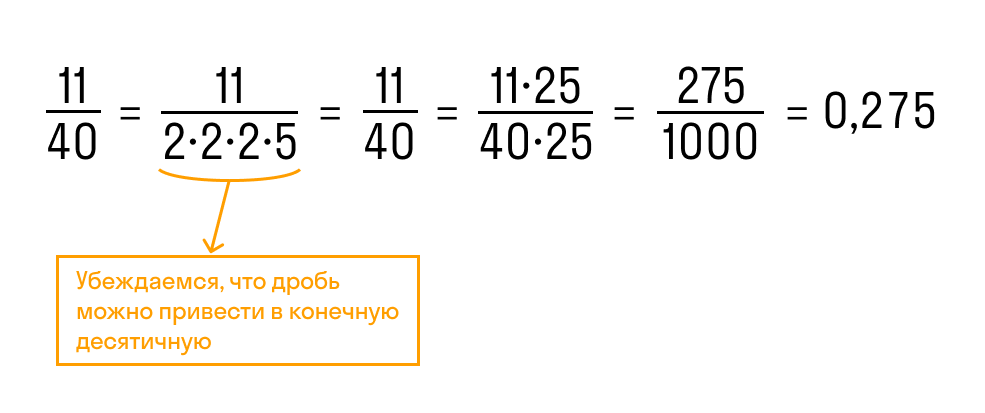
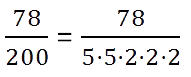
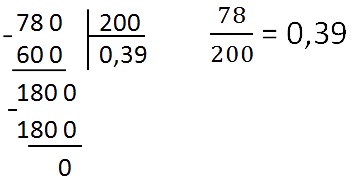
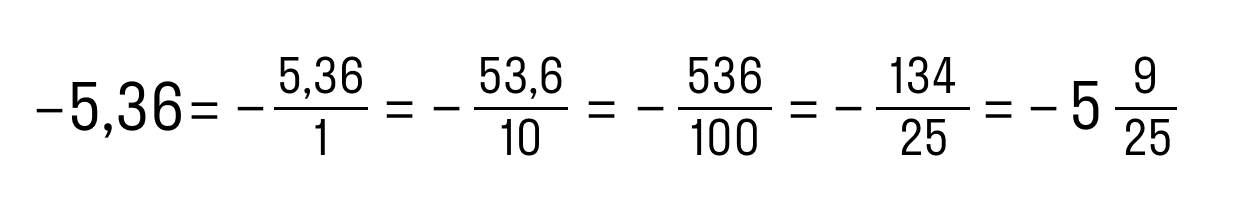
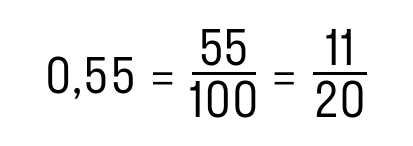

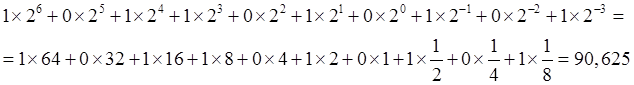 Преобразование дробных десятичных чисел в двоичные
Преобразование дробных десятичных чисел в двоичные | 7450 –
| 7450 –  или читать все.
или читать все.