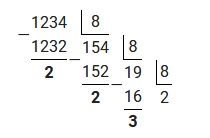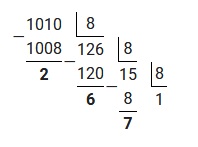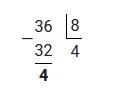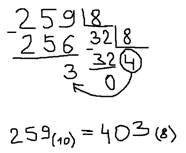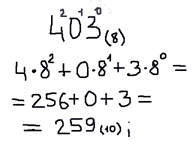Как перевести в восьмеричную систему счисления
Перевод из десятичной системы счисления в восьмеричную
Перед тем как перейти к алгоритму перевода, вспомним алфавит восьмеричной и десятичной системы счисления:
| Основание | Название | Алфавит |
|---|---|---|
| 8 | Восьмеричная | 0, 1, 2, 3, 4, 5, 6, 7 |
| 10 | Десятичная | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 |
Для перевода чисел из десятичной системы в восьмеричную, воспользуемся соответствующим алгоритмом. Важно заметить, что алгоритм перевода целых и дробных чисел будет отличаться.
Алгоритм перевода целых десятичных чисел в восьмеричную систему счисления
Пример 1 : перевести десятичное число 1234 в восьмеричную систему счисления
Для наглядности произведем деление «столбиком». Решение будет выглядеть следующим образом:
Исходя из вышеприведенного алгоритма, полученные остатки необходимо записать в обратном порядке.
Алгоритм перевода десятичной дроби в восьмеричную систему
Пример 2: перевести число 0,1234 в восьмеричную систему.
Решение будет выглядеть следующим образом:
0.1234 ∙ 8 = 0.9872 (0)
0.9872 ∙ 8 = 7.8976 (7)
0.8976 ∙ 8 = 7.1808 (7)
0.1808 ∙ 8 = 1.4464 (1)
0.4464 ∙ 8 = 3.5712 (3)
0.5712 ∙ 8 = 4.5696 (4)
0.5696 ∙ 8 = 4.5568 (4)
0.5568 ∙ 8 = 4.4544 (4)
0.4544 ∙ 8 = 3.6352 (3)
0.6352 ∙ 8 = 5.0816 (5)
0.0816 ∙ 8 = 0.6528 (0)
В данном примере можно продолжить вычисления, но зачастую, такой точности будет достаточно.
Перевод дробного десятичного числа в восьмеричную систему
Для того чтобы перевести десятичное число, содержащее дробную часть, необходимо отдельно перевести целую часть и отдельно дробную.
Пример 3: перевести число 1010,1875 из десятичной системы в восьмеричную
Для решения примера потребуется отдельно перевести 1010 и отдельно 0,1875 из десятичной системы в восьмеричную, используя вышеизложенные алгоритмы. Таким образом переведя 1010, получим:
Перевод десятичной дроби 0,1875 выглядит так:
0.1875 ∙ 8 = 1.5 (1)
0.5 ∙ 8 = 4 (4)
Теперь осталось соединить результаты перевода. Таким образом: 1010.187510=1762.148
Обратите внимание, что данный пример наглядно демонстрирует ситуацию, при которой дробная часть стала равной 0 и дальнейшее вычисление закончилось.
Перевод из двоичной системы счисления в восьмеричную
Для перевода чисел из двоичной системы в восьмеричную, воспользуемся соответствующим алгоритмом. Важно заметить, что алгоритм перевода целых и дробных чисел будет отличаться.
Алгоритм перевода двоичных чисел в восьмеричную систему счисления
Подробно о переводе из двоичной в десятичную систему смотрите на этой странице, о переводе из десятичной в восьмеричную — на смотрите здесь. Для целостного понимания, разберем несколько примеров, но для начала вспомним алфавиты двоичной, восьмеричной и десятичной систем счисления:
| Основание | Название | Алфавит |
|---|---|---|
| 2 | Двоичная | 0, 1 |
| 8 | Восьмеричная | 0, 1, 2, 3, 4, 5, 6, 7 |
| 10 | Десятичная | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 |
Перевод целого двоичного числа в восьмеричную систему счисления
Пример 1: перевести 100100 из двоичной системы в восьмеричную.
Как было сказано выше, необходимо сначала перевести число в десятичное, а полученный ответ в восьмеричное. Решение будет выглядеть следующим образом:
Для перевода двоичного числа 100100 в десятичную систему, воспользуемся формулой:
1001002=1 ∙ 2 5 + 0 ∙ 2 4 + 0 ∙ 2 3 + 1 ∙ 2 2 + 0 ∙ 2 1 + 0 ∙ 2 0 = 1 ∙ 32 + 0 ∙ 16 + 0 ∙ 8 + 1 ∙ 4 + 0 ∙ 2 + 0 ∙ 1 = 32 + 0 + 0 + 4 + 0 + 0 = 3610
Полученное число 36 переведем из десятичной системы счисления в восьмеричную. Для этого, осуществим последовательное деление на 8, до тех пор пока остаток не будет меньше чем 8.
Полученные остатки записываем в обратном порядке, таким образом:
Перевод дробного двоичного числа в восьмеричную систему счисления
Пример 2: перевести 1000010.100 из двоичной в восьмеричную систему счисления.
Общий смысл алгоритма перевода дробного числа, аналогичен алгоритму перевода целого, т.е. вначале переводим в десятичную, а затем в восьмеричную:
1. Для перевода числа 1000010.100 в десятичную систему воспользуемся формулой:
Обратите внимание! Формула перевода дробного числа в десятичную систему, очень похожа на формулу перевода целого, однако немного отличается.
2. Полученное число 66.5 переведем из десятичной системы счисления в восьмеричную. Для этого потребуется перевести вначале целую часть, а затем дробную. Таким образом необходимо:
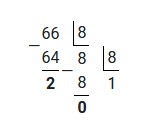
2.1 Для того, чтобы перевести число 66 из десятичной системы счисления в восьмеричную, необходимо осуществить последовательное деление на 8, то тех пор пока остаток не будет меньше чем 8.
Полученные остатки записываем в обратном порядке, таким образом:
2.2 Для перевода десятичной дроби 0.5 в восьмеричную систему, необходимо выполнить последовательное умножение дроби на 8, до тех пор, пока дробная часть не станет равной 0 или пока не будет достигнута заданная точность вычисления. Получаем:
Т.к. дробная часть 0, продолжать умножение не нужно. Ответом станет 0.4, т.е.
2.3. Осталось соединить переведенные части, таким образом:
Перевод чисел из одной системы счисления в другую
Данный конвертер переводит числа между наиболее популярными системами счисления: десятичной, двоичной, восьмеричной, шестнадцатеричной.
Существуют и другие системы счисления, но мы не стали включать их в конвертер из-за низкой популярности.
Для указания системы счисления при записи числа используется нижний индекс, который ставится после числа:
20010 = 110010002 = 3108 = C816
Кратко об основных системах счисления
Десятичная система счисления. Используется в повседневной жизни и является самой распространенной. Все числа, которые нас окружают представлены в этой системе. В каждом разряде такого числа может использоваться только одна цифра от 0 до 9.
Двоичная система счисления. Используется в вычислительной технике. Для записи числа используются цифры 0 и 1.
Восьмеричная система счисления. Также иногда применяется в цифровой технике. Для записи числа используются цифры от 0 до 7.
Перевод в десятичную систему счисления
Перевод из десятичной системы счисления в другие
Делим десятичное число на основание системы, в которую хотим перевести и записываем остатки от деления. Запишем полученные остатки в обратном порядке и получим искомое число.
Переведем число 37510 в восьмеричную систему:
Перевод из двоичной системы в восьмеричную
Так же как и в первом способе разбиваем число на группы. Но вместо преобразований в скобках просто заменим полученные группы (триады) на соответствующие цифры восьмеричной системы, используя таблицу триад:
Перевод из двоичной системы в шестнадцатеричную
Также как и в первом способе разбиваем число на группы по 4 цифры. Заменим полученные группы (тетрады) на соответствующие цифры шестнадцатеричной системы, используя таблицу тетрад:
| Тетрада | 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Цифра | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
Перевод из восьмеричной системы в двоичную
Каждый разряд восьмеричного числа будем делить на 2 и записывать остатки в обратном порядке, формируя группы по 3 разряда двоичного числа. Если в группе получилось меньше 3 разрядов, тогда дополняем нулями. Записываем все группы по порядку, отбрасываем ведущие нули, если имеются, и получаем двоичное число.
Используем таблицу триад:
Каждую цифру исходного восьмеричного числа заменяется на соответствующие триады. Ведущие нули самой первой триады отбрасываются.
Перевод из шестнадцатеричной системы в двоичную
Аналогично переводу из восьмеричной в двоичную, только группы по 4 разряда.
Используем таблицу тетрад:
| Цифра | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Тетрада | 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
Каждую цифру исходного числа заменяется на соответствующие тетрады. Ведущие нули самой первой тетрады отбрасываются.
Перевод из восьмеричной системы в шестнадцатеричную и наоборот
Такую конвертацию можно осуществить через промежуточное десятичное или двоичное число. То есть исходное число сначала перевести в десятичное (или двоичное), и затем полученный результат перевести в конечную систему счисления.
Перевод чисел из десятичной системы счисления в восьмеричную и наоборот.
В этом уроке информатики мы рассмотрим как перевести любое число из десятичной системы счисления в восьмеричную, а затем переведем произвольное число из восьмиричной системы счисления в десятичную, то есть сделаем обратное действие.
Итак в десятичной системе счисления мы пользуемся 10 цифрами с помощью которых можем составить любое число. Это цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
В восьмеричной системе счисления у нас только восемь цифр 0, 1, 2, 3, 4, 5, 6, 7, с помощью которых мы можем составлять любые числа.
В восьмеричной системе счисления после семерки идет цифра 10 т.к. цифры 8 в ней нет. Почему? А потому что когда мы работаем в десятичной системе счисления то когда доходим до 9 то при прибавлении к ней единицы 9+1 получаем, что 9 заменяется на ноль, слева от которого добавляется 1 (к старшему разряду).
Таким образом мы можем попробовать составить небольшую таблицу соответствия чисел десятичной и восьмиричной системы счисления.
Десятичная
Восьмеричная
То есть, смотрите, когда мы выписывали правый столбец (числа в восьмеричной системе счисления) мы руководствовались тем правилом, которое описали выше таблицы. Как только у нас заканчиваются цифры системы счисления мы пишем ноль и добавляем единицу к старшему разряду.
А теперь рассмотрим как перевети число из десятичной системы счисления в восьмеричную. Давайте возьмем число 259 в десятичной системе счисления.
Число в десятичной системе счисления делим на основание степени (восьмерку). Получаем какую то целую часть и остаток. Если целая часть больше либо равна 8, то опять делим на основание степени и получаем целую часть и остаток. Как только целая часть становится меньше восьми, начинаем выписывать, сначала последнюю целую часть, а затем все остатки в обратном порядке. Это и будет число в новой системе счисления, в нашем случае в восьмиричной.
И сделаем обратное преобразование переведем число 403 в восьмеричной системе счисления в десмятичную.
То есть вначале мы нумеруем числа справа налево для того, чтобы затем каждое из чисел в восьмиричной системе счисления умножить на восьмерку в соответствующей степени. Сложив все, мы получим результат в десятичной системе счисления.
Как переводить числа в восьмеричную систему счисления
Во время изучения информатики не всем понятно, как переводить в восьмеричную систему счисления десятичную форму представления. В школьной программе применяется обыкновенная общая методика, но при этом не учитываются умственные способности учеников. Специалисты разработали специальный алгоритм, позволяющий выполнить эту операцию без особых усилий. Однако для начала нужно изучить теорию, а затем перейти к ее практическому применению.
Общие сведения
Для кодирования информации используются различные формы представления данных. Это объясняется тем, что компьютер «не понимает» обыкновенного человеческого языка напрямую. Любая команда переводится в машинный код при помощи специальных алгоритмов кодирования данных. Чтобы в них разобраться, нужно освоить базовые понятия, к которым относятся следующие:
Следует отметить, что каждый пункт необходимо подробно разобрать, поскольку от этого зависит корректность применения алгоритма. Далее нужно ознакомиться с понятием разрядной сетки.
Разрядная сетка
Разрядной сеткой называется совокупность цифр, расположенных в определенном порядке значимости элементов. На первый взгляд, определение является сложным для понимания. Однако это не так. Чтобы в этом убедиться, необходимо разобрать число «126789». Оно состоит из компонентов, которые называются цифрами, где каждая принимает значение из диапазона от 0 до 9. Любая из них находится на определенном месте, а именно:
Следует отметить, что значимость элементов определяется очень просто. Для этого нужно сравнить для примера сотни и единицы. Первые больше, чем вторые. На основании этого примера утверждение о значимости доказано.
Компоненты разрядной сетки можно сложить, т. е. 1*9+10*8+100*7+1000*6+10000*2+100000*1=126789. Каждое число состоит из цифр. В этом и заключается основное отличие между ними. Теперь можно переходить к знакомству с системами счисления.
Виды систем счисления
Системы счисления условно делятся на две группы. К ним относятся следующие:
В первом случае расположение математических символов (цифр) играет важную роль, поскольку влияет на величину числа в целом. Чтобы в этом убедиться, нужно разобрать значение в десятичном формате 192. Для опыта необходимо переставить знаки. При этом получаются пять числовых величин:
Следует отметить, что каждое из них отличается от другого. Все пять чисел можно также сравнить с исходным значением. Из выполненного опыта можно сделать вывод, что расположение компонентов в разрядной сетке имеет значение. К позиционным СС относятся следующие основные формы представления чисел:
Однако существуют и другие формы представления числовых величин, а именно: третичная, четвертичная, пятеричная и т. д. Основным их отличием является основание.
Унарными называются такие СС, какие не зависят от расположения символов. Для примера необходимо вспомнить фильм о Робинзоне Крузо. Он считал дни при помощи обыкновенных палочек, которые чертил на поверхности.
Другим примером является подсчет количества мешков сахара, погруженных на грузовую машину. При загрузке одного мешка бригадир ставит обыкновенный произвольный символ, обозначающий единицу. У каждой системы счисления существует определенный алфавит или символы, используемые для записи цифр и чисел.
Чтобы перевести величину в позиционную восьмеричную СС, необходимо освоить методику конвертации и работы с двоичным кодом.
Двоичный код
Перед тем как начать работу с восьмеричным кодом нужно ознакомиться с двоичным. Чтобы перевести число из десятичной формы в двоичную, требуется воспользоваться следующим алгоритмом:
Обратная операция выполняется по более упрощенной методике. Она имеет такой вид:
Следует отметить, что проверить конвертацию можно при помощи специальных калькуляторов. Последние должны работать с двоичным, восьмеричным и шестнадцатеричным кодами. После освоения материала работы с двоичной формой представления числа можно перейти к восьмеричной.
Восьмеричная форма
Восьмеричная система исчисления применяется в программировании. Однако чтобы в нее перевести десятичную величину, нужно ознакомиться с методикой, позволяющей выполнить эту операцию. Она имеет следующий вид:
Чтобы разобраться в теории, необходимо использовать алгоритм на практическом примере перевода десятичной формы в виде числа 19 в восьмеричный код. Получение искомого результата нужно осуществлять по такой методике:
Для обратного преобразования применяется также определенные правила, составляющие в совокупности отдельный алгоритм. Он выглядит таким образом:
Для примера необходимо рассмотреть величину, равную [23]<8>. Чтобы ее перевести обратно на «человеческий понятный язык» (запись в десятичной форме), следует применить такой алгоритм:
Следует отметить, что в третьем пункте для удобства может не присутствовать нуль, поскольку у двоичного кода есть одно важное правило: если дописывать нули слева, то это действие не повлияет на исходное число.
Кроме того, математики не рекомендуют составлять таблицу для восьмеричной системы счисления, поскольку в этом нет необходимости, как для шестнадцатеричного кода. Для удобства можно записать все методики на отдельные листы бумаги, которые должны находиться постоянно перед глазами ученика.
Таким образом, восьмеричная система представления чисел применяется для кодирования информации в программировании и вычислительной технике. Для этого необходимо получить базовые знания о специальных методиках конвертации величин.