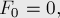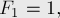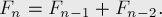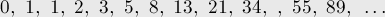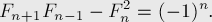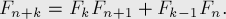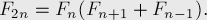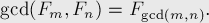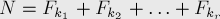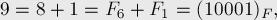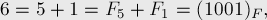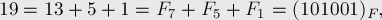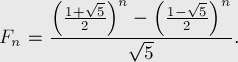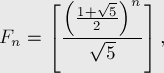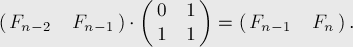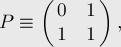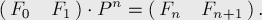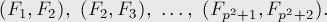Как перевести в систему фибоначчи
Числа Фибоначчи
Определение
Последовательность Фибоначчи определяется следующим образом:
Несколько первых её членов:
История
Эти числа ввёл в 1202 г. Леонардо Фибоначчи (Leonardo Fibonacci) (также известный как Леонардо Пизанский (Leonardo Pisano)). Однако именно благодаря математику 19 века Люка (Lucas) название «числа Фибоначчи» стало общеупотребительным.
Впрочем, индийские математики упоминали числа этой последовательности ещё раньше: Гопала (Gopala) до 1135 г., Хемачандра (Hemachandra) — в 1150 г.
Числа Фибоначчи в природе
Сам Фибоначчи упоминал эти числа в связи с такой задачей: «Человек посадил пару кроликов в загон, окруженный со всех сторон стеной. Сколько пар кроликов за год может произвести на свет эта пара, если известно, что каждый месяц, начиная со второго, каждая пара кроликов производит на свет одну пару?». Решением этой задачи и будут числа последовательности, называемой теперь в его честь. Впрочем, описанная Фибоначчи ситуация — больше игра разума, чем реальная природа.
Индийские математики Гопала и Хемачандра упоминали числа этой последовательности в связи с количеством ритмических рисунков, образующихся в результате чередования долгих и кратких слогов в стихах или сильных и слабых долей в музыке. Число таких рисунков, имеющих в целом 
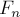
Числа Фибоначчи появляются и в работе Кеплера 1611 года, который размышлял о числах, встречающихся в природе (работа «О шестиугольных снежинках»).
Интересен пример растения — тысячелистника, у которого число стеблей (а значит и цветков) всегда есть число Фибоначчи. Причина этого проста: будучи изначально с единственным стеблем, этот стебель затем делится на два, затем от главного стебля ответвляется ещё один, затем первые два стебля снова разветвляются, затем все стебли, кроме двух последних, разветвляются, и так далее. Таким образом, каждый стебель после своего появления «пропускает» одно разветвление, а затем начинает делиться на каждом уровне разветвлений, что и даёт в результате числа Фибоначчи.
Вообще говоря, у многих цветов (например, лилий) число лепестков является тем или иным числом Фибоначчи.
Также в ботанике известно явление »филлотаксиса». В качестве примера можно привести расположение семечек подсолнуха: если посмотреть сверху на их расположение, то можно увидеть одновременно две серии спиралей (как бы наложенных друг на друга): одни закручены по часовой стрелке, другие — против. Оказывается, что число этих спиралей примерно совпадает с двумя последовательными числами Фибоначчи: 34 и 55 или 89 и 144. Аналогичные факты верны и для некоторых других цветов, а также для сосновых шишек, брокколи, ананасов, и т.д.
Для многих растений (по некоторым данным, для 90% из них) верен и такой интересный факт. Рассмотрим какой-нибудь лист, и будем спускаться от него вниз до тех пор, пока не достигнем листа, расположенного на стебле точно так же (т.е. направленного точно в ту же сторону). Попутно будем считать все листья, попадавшиеся нам (т.е. расположенные по высоте между стартовым листом и конечным), но расположенными по-другому. Нумеруя их, мы будем постепенно совершать витки вокруг стебля (поскольку листья расположены на стебле по спирали). В зависимости от того, совершать витки по часовой стрелке или против, будет получаться разное число витков. Но оказывается, что число витков, совершённых нами по часовой стрелке, число витков, совершённых против часовой стрелки, и число встреченных листьев образуют 3 последовательных числа Фибоначчи.
Впрочем, следует отметить, что есть и растения, для которых приведённые выше подсчёты дадут числа из совсем других последовательностей, поэтому нельзя сказать, что явление филлотаксиса является законом, — это скорее занимательная тенденция.
Свойства
Числа Фибоначчи обладают множеством интересных математических свойств.
Вот лишь некоторые из них:
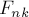
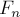
если 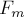
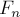


Фибоначчиева система счисления
Теорема Цекендорфа утверждает, что любое натуральное число 
где 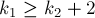
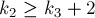

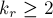
Отсюда следует, что любое число можно однозначно записать в фибоначчиевой системе счисления, например:
причём ни в каком числе не могут идти две единицы подряд.
Нетрудно получить и правило прибавления единицы к числу в фибоначчиевой системе счисления: если младшая цифра равна 0, то её заменяем на 1, а если равна 1 (т.е. в конце стоит 01), то 01 заменяем на 10. Затем «исправляем» запись, последовательно исправляя везде 011 на 100. В результате за линейное время будет получена запись нового числа.
Перевод числа в фибоначчиеву систему счисления осуществляется простым «жадным» алгоритмом: просто перебираем числа Фибоначчи от больших к меньшим и, если некоторое 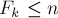
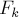

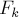

Формула для n-го числа Фибоначчи
Формула через радикалы
Существует замечательная формула, называемая по имени французского математика Бине (Binet), хотя она была известна до него Муавру (Moivre):
Эту формулу легко доказать по индукции, однако вывести её можно с помощью понятия образующих функций или с помощью решения функционального уравнения.
Сразу можно заметить, что второе слагаемое всегда по модулю меньше 1, и более того, очень быстро убывает (экспоненциально). Отсюда следует, что значение первого слагаемого даёт «почти» значение 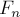
где квадратные скобки обозначают округление до ближайшего целого.
Впрочем, для практического применения в вычислениях эти формулы мало подходят, потому что требуют очень высокой точности работы с дробными числами.
Матричная формула для чисел Фибоначчи
Нетрудно доказать матричное следующее равенство:
Но тогда, обозначая
Таким образом, для нахождения 


Вспоминая, что возведение матрицы в 
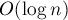

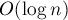
Периодичность последовательности Фибоначчи по модулю
Рассмотрим последовательность Фибоначчи 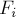

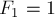
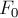
Докажем это от противного. Рассмотрим 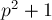

Поскольку по модулю 
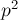
Выберем теперь среди всех таких одинаковых пар две одинаковые пары с наименьшими номерами. Пусть это пары с некоторыми номерами 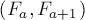
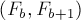
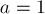
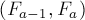
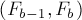
Система счисления на базе ряда Фибоначчи онлайн
| Целое положительное число не больше 1 миллиона |
| Исходное натуральное число |
| Результат кодирования в код Фиббоначи |
| Перевод вычисленного кода в десятиричную систему |
Мы все знаем как можно кодировать число в ту или иную систему счисления: в двоичную, восьмеричную, шестнадцатиричную. В этом материале я познакомлю Вас с кодированием на базе чисел Фиббоначи.
Про эти числа уже говорилось в материале расчет произвольного числа ряда Фибоначчи онлайн и сейчас я только хочу напомнить Вам этот ряд
\(1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946\)
Этим рядом, можно также привести любое натуральное число в совокупность нулей и единиц, как это делается например в двоичной системе.
Алгоритм кодирования (вернее его описание) мы возьмем с википедии без каких либо изменений
«Для кодирования целого числа N :
Но калькулятор который осуществляет кодирование на этой странице построен совсем по другому принципу.
Как минимум не выполняется 4 пункт. Он ставит единицу как маркер окончания слова. В моем калькуляторе этого нет.
Что касается алгоритма.
Фактически, это побочный эффект от реализации алгоритма решения частное решение диофантового уравнения с несколькими неизвестными. Я его(эффект) обнаружил и решил сделать калькулятор.
Калькулятор имеет ограничение сверху в один миллион. Для того что бы понять структуру, применимость кода этого вполне достаточно.
Кроме этого код преобразует полученную совокупность нулей и единиц в десятичную систему по двоичной базе.
Чем же интересен построенный код?
Во первых он избыточен, даже слишком. Для любого числа код Фиббоначи, будет иметь такой вид, что между единицами как минимум(!) будет один ноль.
С одной стороны это плохо. На передачу такого кода понадобится почти в два раза больше времени, чем если бы кодирование осуществлялось двоичной системой.
В чем же плюс: В том, что избыточность кода позволяет нам легко обнаруживать ошибки при передаче. Это незаменимо при плохой связи, при общении с поселениями на различных планетах.
Передача сообщений непрерывным потоком с помощь кодирования Фиббоначи, позволяет в реальном времени (в потоке) исправлять возникшие ошибки, по тому критерию, который был уже озвучен: в коде не может быть рядом стоящих единиц.
Кодирование 8-ми битной таблицы символов ASCII новым кодом потребовало бы 11 разрядов ( 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 ), но туда помещались бы не 256 знаков, а 287 (2*144-1). С учетом уже «встроенной помехоустойчивости» это неплохо, получить еще лишний 31 знак.
Так как букв в алфавите 33, то мы можем зашифровать каждую букву 7-ью битами (1,2,3,5,8,13,21). В этот же размер помещается еще дополнительно 8 знаков(21*2-1-33). Мы можем наш алфавит уменьшить до 31 ( считая что е- ё, и-й одной буквой) и получим что что в 7 бит мы поместили русский алфавит и все цифры.
С английским языком еще проще. Там всего 23 буквы и кодируя 7-ми битным кодом, мы умещаем (не только английский алфавит и все цифры, но и еще 8 символов, например знаки препинания, математические знаки и прочее).
Необычные системы счисления. Фибоначчиева система счисления
В 1202 г. итальянский математик Леонард Пизанский (Leonardo Pisanto, около 1170 – около 1228), известный под именем Фибоначчи (Fibonacci), предложил такую задачу:
Пара кроликов каждый месяц дает приплод – двух кроликов (самца и самку), от которых через два месяца уже получается новый приплод. Сколько кроликов будет через год, если в начале года мы имели одну пару молодых кроликов?
В 1202 г. итальянский математик Леонард Пизанский (Leonardo Pisanto, около 1170 – около 1228), известный под именем Фибоначчи (Fibonacci), предложил такую задачу:
Пара кроликов каждый месяц дает приплод – двух кроликов (самца и самку), от которых через два месяца уже получается новый приплод. Сколько кроликов будет через год, если в начале года мы имели одну пару молодых кроликов?
Числа, соответствующие количеству кроликов составляют последовательность: 1, 1, 2, 3, 5, 8, 13, 21, 34, …
Каждый из членов этой последовательности, начиная с третьего, равен сумме двух предыдущих членов. Эта последовательность называется рядом Фибоначчи, а ее члены – числами Фибоначчи. На уроках математики эти числа связаны с так называемым золотым сечениям. На уроках информатики числа Фибоначчи широко используются для объяснения рекурсивной зависимости, где F(n)=F(n-1) + F(n-2), при n³3, F(1)=1 и F(2)=1.
Таким образом, получаем, что:
В итоге, получаем числа: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, …
Но мало кто знает, что числа Фибоначчи используются в так называемой Фибоначчиевой системе счисления.
В старшей школе при изучении темы «Кодирование информации» я предлагаю обучающимся познакомиться с Фибоначчиевой системой счисления в целях расширения представлений о системах счисления и обобщения принципа позиционности.
Обучающиеся узнают, что принцип разложения любого числа в Фибоначчиевой системе счисления основывается на уже знакомом им переводе десятичного числа в двоичное «Методом подбора степеней числа 2»: исходное десятичное число представляют в виде суммы степеней числа 2, в этой сумме слагаемые выстраивают от большего к меньшему. Затем те степени двойки, которые имеются, заменяются 1, а те, которых нет заменяются на 0.
Например, число 37 будет представлено в двоичной системе счисления, как 100101 согласно разложению:
| исходное десятичное число | степени числа «два» | |||||
| 32 | 16 | 8 | 4 | 2 | 1 | |
| 37 | 1 | 0 | 0 | 1 | 0 | 1 |
Например, число 5 в десятичной системе счисления может быть записано как 110Fib (5 = 1 · 3 + 1 · 2 + 0 · 1).
Разложение (вариант 1)
| исходное десятичное число | Базисные числа фибоначчиевой системы счисления | ||
| 3 | 2 | 1 | |
| 5 | 1 | 1 | 0 |
и 1000Fib (5 = 1 · 5 + 0 · 3 + 0 · 2 + 0 · 1), разложение (вариант 2)
| исходное десятичное число | Базисные числа фибоначчиевой системы счисления | |||
| 5 | 3 | 2 | 1 | |
| 5 | 1 | 0 | 0 | 0 |
Причем, правильным считается второе разложение, где в записи нет двух подряд идущих единиц. В этом случае каждое натуральное число в фибоначчиевой системе счисления записывается единственным образом.
В качестве закрепления изученного обучающимся предлагается освоить перевод чисел в фибоначчиевой системе счисления из десятичной и в десятичную систему счисления (освоить прямой и обратный перевод).
Задание 1. Найдите все способы перевода следующих чисел из десятичной системы счисления в фибоначчиеву, например, чисел 37 и 25.
Вариант решения обучающегося: Перевод числа из десятичной системы счисления в фибоначчиевую:
| исходное десятичное число | Базисные числа фибоначчиевой системы счисления | |||||||
| 34 | 21 | 13 | 8 | 5 | 3 | 2 | 1 | |
| 37 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
3710 = 34 + 3 = 1*34+0*21+0*13+0*8+0*5+1*3+0*2+0*1= 10000100Fib
| исходное десятичное число | Базисные числа фибоначчиевой системы счисления | |||||||
| 21 | 13 | 8 | 5 | 3 | 2 | 1 | ||
| 25 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | |
2510 = 21 + 3 + 1 = 1*21+0*13+0*8+0*5+1*3+0*2+1*1=100101Fib
Задание 2. Переведите в десятичную систему числа, записанные в фибоначчиевой системе, например числа: 10010101 и 101010101.
Вариант решения обучающегося: Перевод числа из фибоначчиевой системы счисления в десятичную:
| неизвестное десятичное число | Базисные числа фибоначчиевой системы счисления | |||||||
| 34 | 21 | 13 | 8 | 5 | 3 | 2 | 1 | |
| ? | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 1 |
| неизвестное десятичное число | Базисные числа фибоначчиевой системы счисления | ||||||||
| 55 | 34 | 21 | 13 | 8 | 5 | 3 | 2 | 1 | |
| ? | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
Необходимо отметить, что, хотя для записи числа в этой системе счисления используются только цифры 0 и 1, эту запись нельзя считать двоичным представлением числа.
Список литературы:
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.