ПР 10 Перевод чисел из десятичной системы счисления в другие системы счисления

Цель : Сформировать умение переводить числа из десятичной системы счисления в другие.

Набор этих цифр называется алфавитом системы счисления.

Различают позиционные и непозиционные системы счисления.

Если для каждого числа системы счисления выполняется правило: вес цифры (ее значе­ние) зависит от положения цифры в числе, такая система счисления называется позицион­ной. Если хотя бы для одного числа это правило не выполняется, система счисления называ­ется непозиционной.

Количество цифр в позиционной системе счисления называется основанием системы счисления.

При записи чисел в различных системах счисления принято записывать основание систе­мы счисления справа внизу возле числа. Например, число 6 в восьмеричной системе счисле­ния записывают: 68. (Если основание системы счисления справа внизу возле числа не указа­но, считается, что это десятичная система счисления.)

Для перевода десятичного числа в другую систему счисления необходимо:

1) делить нацело с остатком число на нужное основание системы счисления;

2) получившееся частное (целое) тоже делить нацело с остатком на это основание;

3) продолжать деления до тех пор, пока частное не получится меньше основания системы счисления;

4) выписать последнее частное и остатки в порядке, обратном их получению

П еревод из десятичной системы счисления в двоичную:

Задача 1: Переведите число 25 из десятичной системы счисления в двоичную

25 10 _________ 2

Делим с остатком на 2 до тех пор пока не получим частное 1.

25:2=12(ост 1) 12:2=6 ( ост 0) 6:2=3(ост 0) 3:2=1(ост 1)

На этом деление заканчиваем, т.к. 1 на 2 не делится нацело

Выпишем последнее частное и остатки в обратном порядке.

Ответ: 25 10 11001 2

П еревод из десятичной системы счисления в троичную,……, восьмеричную:

Делим на то число, какое основание у новой системы счисления.

Например, для перевода в троичную систему делим на 3, для перевода в шестеричную систему делим на 6, для перевода в восьмеричную систему делим на 8.

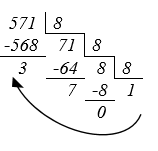
Задача 2: Переведите число 571 из десятичной системы счисления в восьмеричную

571 10 _________ 8

Делим с остатком на 8 до тех пор пока не получим частное меньшее 8.

Выпишем последнее частное и остатки в обратном порядке.

Ответ: 571 10 1073 8

Задача 3: Переведите число 357 из десятичной системы счисления в троичную

357 10 _________ 3

Делим с остатком на 3 до тех пор пока не получим частное меньшее 3.

Выпишем последнее частное и остатки в обратном порядке.

Ответ: 357 10 111020 3

Задача 4: Переведите число 123 из десятичной системы счисления в шестеричную

123 10 _________ 6

Делим на 6 до тех пор пока не получим частное меньшее 6.

Выпишем последнее частное и остатки в обратном порядке.

Ответ: 123 10 323 6

П еревод из десятичной системы счисления в шестнадцатеричную

Делим на 16 до тех пор пока не получим число меньшее 16.

7467 10 _________ 16

Делим на 16 до тех пор пока не получим число меньшее 16.

Выпишем остатки в обратном порядке,

Ответ: 7467 10 1 D 2 B 16

Переведите числа в указанные системы счисления.

По окончании урока сдайте тетрадь преподавателю для проверки вычислений.

По окончании работы, нажмите кнопку Ответить, проверьте результаты своей работы. При наличии времени, исправьте ошибки.

В форму обратной связи введите свою Фамилию Имя, № группы, адрес электронной почты и перешлите результат выполнения практической работы преподавателю.

По окончании урока сдайте тетрадь преподавателю для проверки вычислений.

Источник

Перевод чисел в различные системы счисления с решением

Исходное число записано в -ой системе счисления.

Хочу получить запись числа в -ой системе счисления.

Системы счисления

Системы счисления делятся на два типа: позиционные и не позиционные. Мы пользуемся арабской системой, она является позиционной, а есть ещё римская − она как раз не позиционная. В позиционных системах положение цифры в числе однозначно определяет значение этого числа. Это легко понять, рассмотрев на примере какого-нибудь числа.

Пример 1. Возьмём число 5921 в десятичной системе счисления. Пронумеруем число справа налево начиная с нуля:

Число:	5	9	2	1
Позиция:	3	2	1	0

Пример 2. Рассмотрим вещественное десятичное число 1234.567. Пронумеруем его начиная с нулевой позиции числа от десятичной точки влево и вправо:

Число:	1	2	3	4	5	6	7
Позиция:	3	2	1	0	-1	-2	-3

Перевод чисел из одной системы счисления в другую

Наиболее простым способом перевода числа с одной системы счисления в другую, является перевод числа сначала в десятичную систему счисления, а затем, полученного результата в требуемую систему счисления.

Перевод чисел из любой системы счисления в десятичную систему счисления

Для перевода числа из любой системы счисления в десятичную достаточно пронумеровать его разряды, начиная с нулевого (разряд слева от десятичной точки) аналогично примерам 1 или 2. Найдём сумму произведений цифр числа на основание системы счисления в степени позиции этой цифры:

Перевод чисел из десятичной системы счисления в другую систему счисления

Для перевода чисел из десятичной системы счисления в другую систему счисления целую и дробную части числа нужно переводить отдельно.

Перевод целой части числа из десятичной системы счисления в другую систему счисления

Целая часть переводится из десятичной системы счисления в другую систему счисления с помощью последовательного деления целой части числа на основание системы счисления до получения целого остатка, меньшего основания системы счисления. Результатом перевода будет являться запись из остатков, начиная с последнего.

Рассмотрим перевод правильных десятичных дробей в различные системы счисления.

Перевод дробной части числа из десятичной системы счисления в другую систему счисления

Напомним, правильной десятичной дробью называется вещественное число с нулевой целой частью. Чтобы перевести такое число в систему счисления с основанием N нужно последовательно умножать число на N до тех пор, пока дробная часть не обнулится или же не будет получено требуемое количество разрядов. Если при умножении получается число с целой частью, отличное от нуля, то целая часть дальше не учитывается, так как последовательно заносится в результат.

Programforyou — это сообщество, в котором Вы можете подтянуть свои знания по программированию, узнать, как эффективно решать те или иные задачи, а также воспользоваться нашими онлайн сервисами.

Источник

Изменение системы счисления

Изменение основания для позиционных систем счисления

В позиционной системе счисления с основанием q число может быть представлено в виде полинома

где коэффициенты a_i – это цифры системы счисления с основанием q.

Например, в десятичной системе счисления

Например, нужно найти минимальное основание системы счисления, в которой записано число 7832. Так как максимальная цифра равна 8, то минимальное значение q = 8 + 1 = 9.

Основанием системы счисления может быть, в принципе, любой число: целое, отрицательное, рациональное, иррациональное, комплексное и т.д. Будем рассматривать только положительные целые основания.

Особый интерес для нас будут представлять основание 2 и основания, являющиеся степенью двойки – 8 и 16.

В случае, если основание с. с. больше десяти, то новые цифры берутся по порядку из алфавита. Например, для 16-ричной системы это будут цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.

Перевод целой части десятичной системы счисления

Первый способ перевода из десятичной системы счисления в n-ричную заключается в последовательном делении числа на новое основание.

Собираем в обратном порядке, сначала последнее значение (это 0), потом сверху вниз все остатки. Получаем 0A3 = A3

Собираем обратно, получаем 10723

Собираем вместе: 0D15 = D15

Собираем 01000100001 = 1000100001

Перевод на бумаге обычно осуществляется делением в столбик. Пока деление не приведёт к нулю, каждый следующий ответ делится на основание с. с. В конце, из остатков от деления собирается ответ.

Перевод из десятичной системы счисления в двоичную на бумаге

Например, 129 очевидно 128 + 1 = 2 7 + 1 = 10000001₂

Перевод в десятичную систему счисления целой части

1∙q 4 + 0∙q 3 + 7∙q 2 + 2∙q 1 + 3∙q 0 = 1∙8 4 + 0 + 7∙8 2 + 2∙8 + 3 = 1∙4096 + 7∙64 + 2∙8 + 3 = 4563

D∙16 2 + 1∙16 1 +5∙16 0 = 13∙256 + 16 + 5 = 3349

2 9 + 2 5 + 1 = 512 + 32 + 1 = 545.

Перевод на бумаге обычно осуществляется следующим образом. Над каждой цифрой по порядку пишут номер степени. Затем уже выписывают все слагаемые.

Перевод из шестеричной системы счисления в десятичную на бумаге

Перевод дробной части из десятичной системы

Во время перевода дробной части часто случается ситуация, когда конечная десятичная дробь превращается в бесконечную. Поэтому обычно при переводе указывается точность, с которой необходимо переводить. Перевод осуществляется путём последовательного умножения дробной части на основание системы счисления. Целая часть при этом откидывается и входит в состав дроби.

0 – дальнейшее умножение будет давать только нули
Собираем сверху вниз, получаем 0.101

0.2 … получим периодическую дробь
Собираем, получаем 0.0100110011001… = 0.0(1001)

Перевод дробной части в десятичную систему

Осуществляется аналогично переводу целой части, путём домножения цифры разряда на основание в степени, равной положению разряда в числе.

Перевод из произвольной системы счисления в произвольную

Перевод из произвольной системы счисления в произвольную с. с. осуществляется с помощью десятичной с. с.

1221201₃ = 1∙3 6 + 2∙3 5 + 2∙3 4 + 1∙3 3 + 2∙3 2 + 1 = 729 + 2∙243 + 2∙81 + 27 + 9 + 1 = 1414₁₀

Родственные системы счисления

Системы счисления называют родственными, когда их основания являются степенями одного числа. Например, 2, 4, 8, 16. Перевод между родственными системами счисления можно осуществлять, воспользовавшись таблицей

Таблица для перевода между родственными системами счисления с базой 2

10	2	4	8	16
0	0000	000	00	0
1	0001	001	01	1
2	0010	002	02	2
3	0011	003	03	3
4	0100	010	04	4
5	0101	011	05	5
6	0110	012	06	6
7	0111	013	07	7
8	1000	020	10	8
9	1001	021	11	9
10	1010	022	12	A
11	1011	023	13	B
12	1100	030	14	C
13	1101	031	15	D
14	1110	032	16	E
15	1111	033	17	F

Для перевода из одной родственной системы счисления в другую, сначала нужно перевести число в двоичную систему. Для перевода в двоичную систему счисления каждая цифра числа подменяется на соответствующую двойку (для четверичной), тройку (для восьмеричной) или четвёрку (для шестнадцатеричной).

Для 123₄ единица подменяется на 01, двойка на 10, тройка нa 11, получаем 11011₂

Для 5721₈ соответственно 101, 111, 010, 001, итого 101111010001₂

Для E12₁₆ получим 111000010010₂

Для перевода из двоичной системы следует разбить число на двойки (4-я), тройки (8-я) или четвёрки чисел (16-я), а затем подменить на соответствующие значения.

110100101₂ = 0001.1010.0101 = 1A5₁₆

Переход из одной родственной системы в другую осуществляется транзитом через наименьшее основание, в нашем случае через двойку.

33232₄ → 1111101110₂ → 0011.1110.1110 → 3EE₁₆

Понятно, что все эти рассуждения применимы и для систем счисления 3, 9, 21, 81 и 5, 25, 125 и т.п.

Источник

Шестеричная система счисления примеры

Сложение и вычитание

Таблица 1 – Сложение в двоичной системе

Например, таблица сложения в шестеричной системе счисления:

Таблица 2 – Сложение в шестеричной системе

Сложение любых двух чисел, записанных в системе счисления с основанием с, производится так же, как в десятичной системе, по разрядам, начиная с первого разряда, с использованием таблицы сложения данной системы. Складываемые числа подписываются одно за другим так, чтобы цифры одинаковых разрядов стояли по вертикали. Результат сложения пишется под горизонтальной чертой, проведенной ниже слагаемых чисел. Так же как при сложении чисел в десятичной системе, в случае, когда сложение цифр в каком-либо разряде дает число двузначное, в результат пишется последняя цифра этого числа, а первая цифра прибавляется к результату сложения следующего разряда.

Можно обосновать указанное правило сложения чисел, используя представление чисел в виде:

Разберем один из примеров:

Последовательно выделяем слагаемые по степени основания 7, начиная с низшей, нулевой, степени.

Вычитание производится также по разрядам, начиная с низшего, причем если цифра уменьшаемого меньше цифры вычитаемого, то из следующего разряда уменьшаемого «занимается» единица и из полученного двузначного числа вычитается соответствующая цифра вычитаемого; при вычитании цифр следующего разряда в этом случае нужно мысленно уменьшить цифру уменьшаемого на единицу, если же эта цифра оказалась нулем (и тогда уменьшение ее невозможно), то следует «занять» единицу из следующего разряда и затем произвести уменьшение на единицу. Специальной таблицы для вычитания составлять не нужно, так как таблица сложения дает результаты вычитания.

Умножение и деление

Для выполнения действий умножения и деления в системе с основанием с составляется таблица умножения однозначных чисел.

Таблица 3 – Умножение однозначных чисел

Таблица 4 – Умножение в шестеричной системе счисления

Умножение двух произвольных чисел в системе с основанием с производится так же, как в десятичной системе – «столбиком», то есть множимое умножается на цифру каждого разряда множителя (последовательно) с последующим сложением этих промежуточных результатов.

При умножении многозначных чисел в промежуточных результатах индекс основания не ставится:

Деление в системах с основанием с производится углом, так же, как в десятичной системе счисления. При этом используется таблица умножения и таблица сложения соответствующей системы. Сложнее дело обстоит, если результат деления не является конечной с-ичной дробью (или целым числом). Тогда при осуществлении операции деления обычно требуется выделить непериодическую часть дроби и ее период. Умение выполнять операцию деления в с-ичной системе счисления полезно при переводе дробных чисел из одной системы счисления в другую.

Перевод чисел из одной системы счисления в другую

Существует много различных способов перевода чисел из одной системы счисления в другую.

Для получения записи числа N в системе с основанием h следует представить его в виде:

Войти

Шестеричная система счисления

На русских счетах есть особый ряд из четырёх костяшек. Выше находятся рубли, ниже два ряда копеек (Существует ещё вариант с тремя рядами снизу. Он помогает считать тысячные, но это только для математиков). Особый ряд нужен для подсчёта четвертинок. Число десять легко поделить пополам – для этого служат чёрные костяшки в середине ряда, но уже деление на четыре части требует манипуляций на двух рядах. Про деление на три лучше и не вспоминать, оно в десятичной системе записывается бесконечным числом цифр, а значит не может быть сделано на счётах.

В этот момент популяризаторы математики тяжело вздыхают: «Как жаль, что у человека на руке пять пальцев, а не шесть. Сложись иначе и мы бы считали не десятками, а дюжинами». Действительно, дюжина существенно удобнее в быту, поскольку легко делится на два, на три и на четыре. Она, конечно, не делится на пять, но деление на пять частей довольно редкий случай в торговле или в разрезании листа бумаги на открытки.

Надо заметить, что пять пальцев действительно повлияли на традиционные системы счёта.

Возьмём к примеру русский язык: один дом, два дом(А), три дом (А), четыре дом (А), но: пять дом(ОВ).

Римская запись чисел колебалась между пятью и десятью: I,II,III,IIII (IV – сокращённая на одну черту запись), V. Потом комбинации V и I, затем X. Продолжая дальше мы встречаем десять пятёрок L и десять десяток C. Пять пятёрок римляне пропустили, а зря.

Похожая система была и у индейцев майя, которые комбинировали единицы точки и пятёрки чёрточки:

Сегодня, пока я лежал в кресле стоматолога и пытался занять себя чем-нибудь полезным, мне в голову пришла мысль, что счёт шестёрками на пальцах даже более естественен, чем счёт пятёрками.

Подумайте об обычной десятичной записи: у нас есть цифры от 0 до 9, а второй разряд мы используем для записи первого числа (10), для которого у нет своей цифры.

Теперь следите за руками. Вот естественная запись чисел от нуля до шести

Дальше всё продолжается в том же духе. Вот семь, одиннадцать и искомая дюжина.

Если вы попробуете выполнить на пальцах сложение и вычитание, то обнаружите, что они происходят естественнее, чем если бы мы откладывали на левой руке традиционные пятёрки.

Если бы у французских математиков, вводивших революционную метрическую систему мер было бы чуть больше воображения, то наполеоновская Европа перешла бы на двенадцатеричную систему мер, а дальше к ней с удовольствием подтянулись бы и англоговорящие страны, поскольку в шиллинге 12 пенсов, в футе 12 дюймов и это естественно!

В комментариях подсказали про ещё один (десятичный) вариант «Кафрский счёт»

Войти

Шестеричная система счисления

На русских счетах есть особый ряд из четырёх костяшек. Выше находятся рубли, ниже два ряда копеек (Существует ещё вариант с тремя рядами снизу. Он помогает считать тысячные, но это только для математиков). Особый ряд нужен для подсчёта четвертинок. Число десять легко поделить пополам – для этого служат чёрные костяшки в середине ряда, но уже деление на четыре части требует манипуляций на двух рядах. Про деление на три лучше и не вспоминать, оно в десятичной системе записывается бесконечным числом цифр, а значит не может быть сделано на счётах.

В этот момент популяризаторы математики тяжело вздыхают: «Как жаль, что у человека на руке пять пальцев, а не шесть. Сложись иначе и мы бы считали не десятками, а дюжинами». Действительно, дюжина существенно удобнее в быту, поскольку легко делится на два, на три и на четыре. Она, конечно, не делится на пять, но деление на пять частей довольно редкий случай в торговле или в разрезании листа бумаги на открытки.

Надо заметить, что пять пальцев действительно повлияли на традиционные системы счёта.

Возьмём к примеру русский язык: один дом, два дом(А), три дом (А), четыре дом (А), но: пять дом(ОВ).

Римская запись чисел колебалась между пятью и десятью: I,II,III,IIII (IV – сокращённая на одну черту запись), V. Потом комбинации V и I, затем X. Продолжая дальше мы встречаем десять пятёрок L и десять десяток C. Пять пятёрок римляне пропустили, а зря.

Похожая система была и у индейцев майя, которые комбинировали единицы точки и пятёрки чёрточки:

Сегодня, пока я лежал в кресле стоматолога и пытался занять себя чем-нибудь полезным, мне в голову пришла мысль, что счёт шестёрками на пальцах даже более естественен, чем счёт пятёрками.

Подумайте об обычной десятичной записи: у нас есть цифры от 0 до 9, а второй разряд мы используем для записи первого числа (10), для которого у нет своей цифры.

Теперь следите за руками. Вот естественная запись чисел от нуля до шести

Дальше всё продолжается в том же духе. Вот семь, одиннадцать и искомая дюжина.

Если вы попробуете выполнить на пальцах сложение и вычитание, то обнаружите, что они происходят естественнее, чем если бы мы откладывали на левой руке традиционные пятёрки.

Если бы у французских математиков, вводивших революционную метрическую систему мер было бы чуть больше воображения, то наполеоновская Европа перешла бы на двенадцатеричную систему мер, а дальше к ней с удовольствием подтянулись бы и англоговорящие страны, поскольку в шиллинге 12 пенсов, в футе 12 дюймов и это естественно!

В комментариях подсказали про ещё один (десятичный) вариант «Кафрский счёт»

Источник