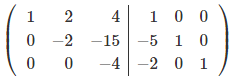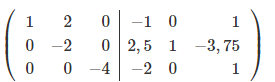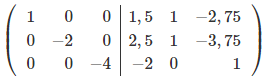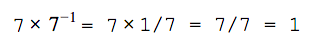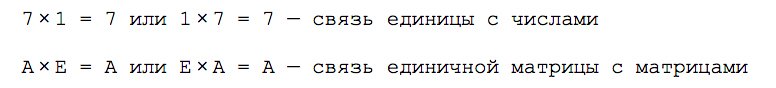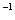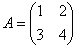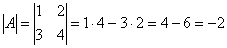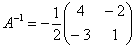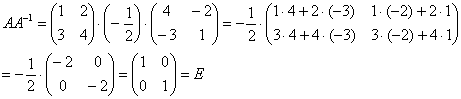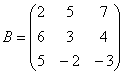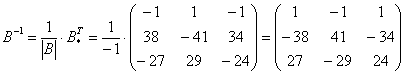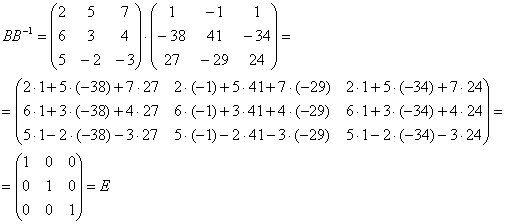Как перевести матрицу в обратную

Обратная матрица с помощью элементарных преобразований

Для того что бы найти обратную матрицу можно использовать два метода: с помощью алгебраических дополнений (метод присоединённой (союзной) матрицы) или элементарных преобразований (метод Жордано-Гаусса). Рассмотрим как найти обратную матрицу с помощью элементарных преобразований.

Алгоритм нахождения обратной матрицы с помощью элементарных преобразований:

Пример

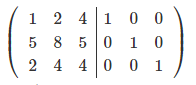
Рассмотрим данный метод на примере. Дана матрицы 3х3:

Допишем к нашей матрице слева единичную матрицу.

Чтобы сделать нули под элементом a₁₁, вычтем 1-ую строку из всех строк, что расположены ниже её, при чём, для того, чтобы работать с меньшими числами, поделим каждую из этих строк на a₁₁.

Чтобы сделать нули над элементом a₃₃, вычтем 3-ую строку с всех строк, что расположены выше её, при чём, для того, чтобы работать с меньшими числами, поделим каждую из этих строк на a₃₃.

Чтобы сделать нули над элементом a₂₂, вычтем 2-ую строку с всех строк, что расположены выше её, при чём, для того, чтобы работать с меньшими числами, поделим каждую из этих строк на a₂₂.

Поделим каждую строку на элемент, который стоит на главной диагонали.

Источник

Обратная матрица.

Метод обратной матрицы.

Метод обратной матрицы – это один из самых распространенных методов решения матриц и применяется для решения систем линейных алгебраических уравнений (СЛАУ) в случаях, когда число неизвестных соответствует количеству уравнений.

Суть метода обратной матрицы.

Пусть есть система n линейных уравнений с n неизвестными:

Такую систему можно записать как матричное уравнение A* X = B,

где – матрица системы,

– столбец неизвестных,

– столбец свободных коэффициентов.

Обратная матрица к матрице A существует лишь тогда, когда det A ≠ 0. Ввиду этого при решении СЛАУ методом обратной матрицы первым делом находится det A. Если det A ≠ 0, то у системы есть только одно решение, которое можно получить методом обратной матрицы, если же det A = 0, то такая система методом обратной матрицы не решается.

Решение обратной матрицы.

Последовательность действий для решения обратной матрицы:

Приведенный ниже алгоритм решения обратной матрицы по сути такой же, как и приведенный выше, разница только в нескольких шагах: первым делом определяем алгебраические дополнения, а уже после этого вычисляем союзную матрицу C.

Нахождение обратной матрицы.

Нахождение обратной матрицы – это лучше всего делать с помощью присоединённой матрицы.

Теорема: Если к квадратной матрице с правой стороны приписать единичную матрицу такого же порядка и при помощи элементарных преобразований над строками преобразовать начальную матрицу, стоящую слева, в единичную, то полученная с правой стороны будет обратной к начальной.

Пример нахождения обратной матрицы.

Задание. Для матрицы найти обратную методом присоединенной матрицы.

Решение. Дописываем к заданной матрице А справа единичную матрицу 2го порядка:

Из 1й строки вычитаем 2ю:

От второй строки отнимаем 2 первых:

1ю и 2ю строки меняем местами:

От 2й строки отнимаем 2 первых:

Вторую строку умножаем на (-1), а к первой строке добавляем 2ю:

Итак, слева имеем единичную матрицу, а, значит, матрица, которая стоит справа, будет обратной к заданной изначально.

Т.о., имеем .

Ответ после нахождения обратной матрицы:

Замечание. Если на каком-либо этапе в «левой» матрице образуется нулевая строка, значит, что заданная изначально не имеет обратной.

Источник

Что такое обратная матрица

Сложная тема из линейной алгебры.

Недавно мы начали говорить о линейной алгебре и матрицах. Сначала всё было хорошо и легко:

Но начав заниматься линейной алгеброй, бывает трудно остановиться. Сегодня мы познакомимся с обратной матрицей и научимся её вычислять. Это навык, который в будущем нам пригодится для решения матричных уравнений.

С точки зрения арифметики материал не сложный. Но он требует вдумчивого чтения для понимания правил. В итоге статья довольно большая, мозги кипят и танки наши быстры.

Читать ли эту статью?

❌ Если вам нужны простые быстрые решения для жизни — нет, можно объявить, что у вас сегодня выходной.

✅ Если вашему мозгу не хватает вызова и новых горизонтов — велком ту зе матрикс.

Обратное — это как?

В математике есть взаимно обратные числа. Они получаются так: вы берёте какое-то число, добавляете отрицательную степень и получаете обратное число:

Обратные числа при умножении друг на друга всегда дают единицу:

Обратная матрица

В линейной алгебре есть обратные матрицы. По свойствам они напоминают обратные числа: если обычную матрицу умножить на обратную к ней, получится единичная матрица.

Единичная матрица работает как единица с числами: если умножить любое число на единицу, получится исходное число; если умножить любую матрицу на единичную матрицу — получится исходная матрица:

Единичная матрица состоит из единиц и нулей: на диагонали находятся единицы; остальные элементы — нули. Единичные матрицы не используются при расчёте обратных матриц, но без них не получится решать матричные уравнения.

Пример квадратной единичной матрицы размером 5×5. Единичная матрица может быть любого размера — состоять из любого количества строк и столбцов

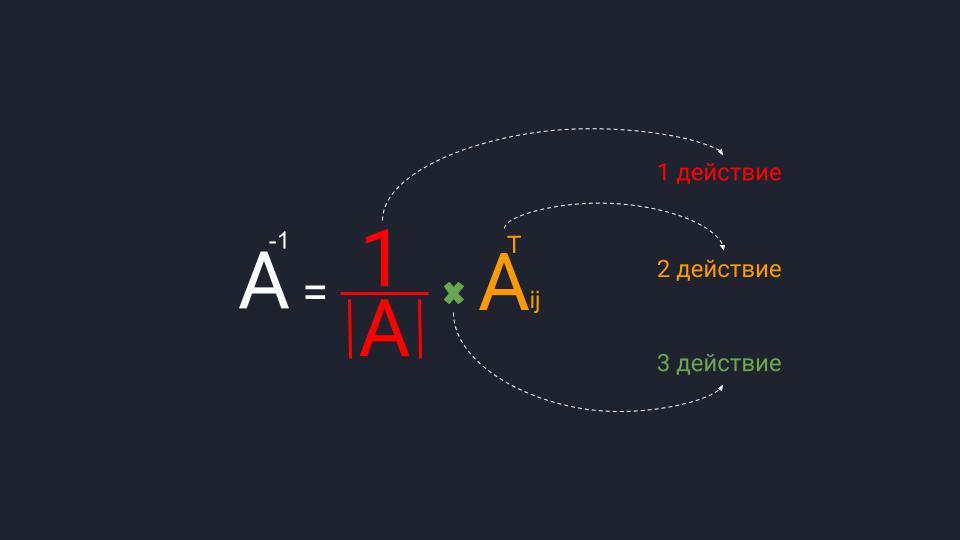
Как рассчитать обратную матрицу

Для расчёта обратной матрицы нужно выполнить три действия. Пока что не обращайте внимание на термины:

Далее мы по порядку во всём разберёмся.

Формула расчёта обратной матрицы: |A| — матричный определитель; Aᵀᵢⱼ — матрица алгебраических дополнений

Определитель — это особое число, которое «определяет» свойства матрицы.

Порядок вычисления определителя зависит от размера матрицы, которому он соответствует — чем больше матрица, тем сложнее считать определитель. Мы только знакомимся с матрицами, поэтому остановимся на определителях второго и третьего порядка — они подходят для квадратных матриц размером 2×2 и 3×3.

Чтобы найти определитель второго порядка, нам достаточно умножить элементы главной диагонали и вычесть из значения произведение чисел второй диагонали.

Формула для расчёта определителя второго порядка

Пример расчёта определителя второго порядка

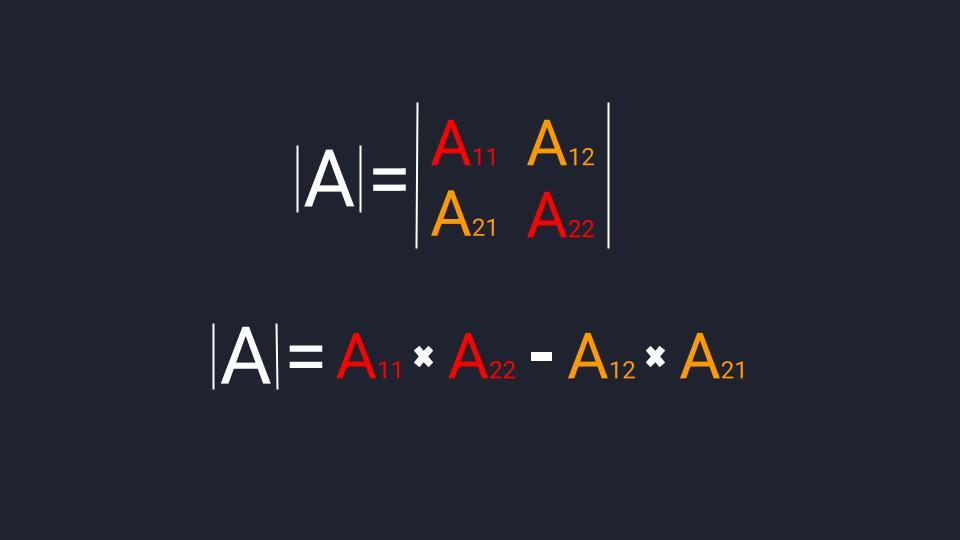
Определитель третьего порядка находится путём умножения диагоналей на треугольники. Здесь много операций, поэтому формулу соберём по частям.

Сначала работаем по главной диагонали: идём от верхнего левого элемента и движемся к правому нижнему элементу. Перемножаем элементы между собой.

Считаем определитель третьего порядка: 1-й этап — главная диагональ

Прибавляем к произведению элементов первой диагонали произведение первого треугольника. Основание первого треугольника находится параллельно главной диагонали и состоит из элементов А₂₁ и А₃₂. Вершина — элементА₁₃.

Считаем определитель третьего порядка: 2-й этап — первый треугольник

Прибавляем к полученному результату произведение второго треугольника, в котором основание состоит из элементов А₁₂ и А₂₃, а вершина — А₃₁.

Считаем определитель третьего порядка: 3-й этап — второй треугольник

Вычитаем из полученного значения произведение элементов второй диагонали. Вторая диагональ начинается в левом нижнем углу и идёт в правый верхний угол.

Считаем определитель третьего порядка: 4-й этап — вторая диагональ

Вычитаем произведение элементов третьего треугольника, в котором основание — элементы А₁₂ и А₂₁, а вершина — А₃₃.

Считаем определитель третьего порядка: 5-й этап — третий треугольник

Последний шаг: вычитаем произведение четвёртого треугольника, с основанием из элементов А₂₃ и А₃₂ и вершиной А₁₁.

Считаем определитель третьего порядка: 6-й этап — четвёртый треугольник

Общий вид формулы для расчёта определителя третьего порядка

Пример расчёта определителя третьего порядка

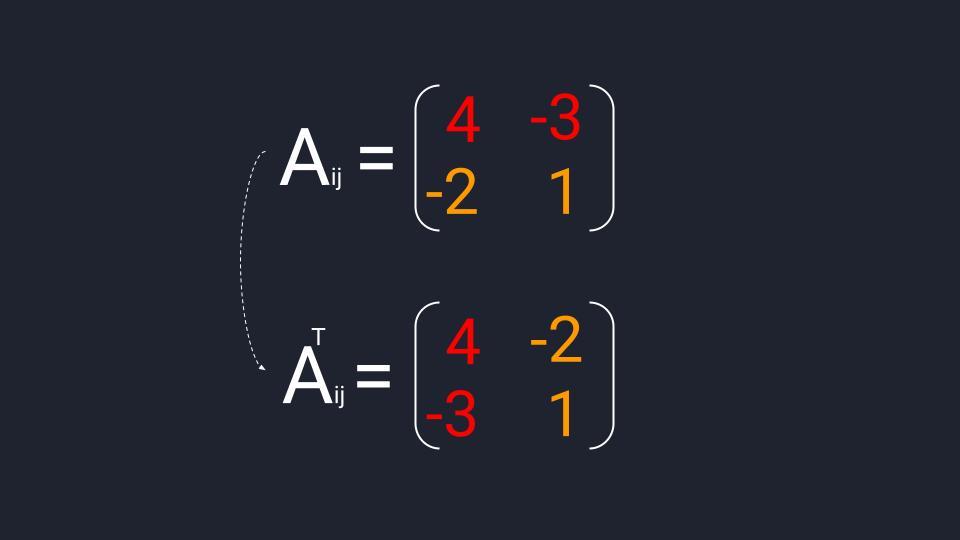
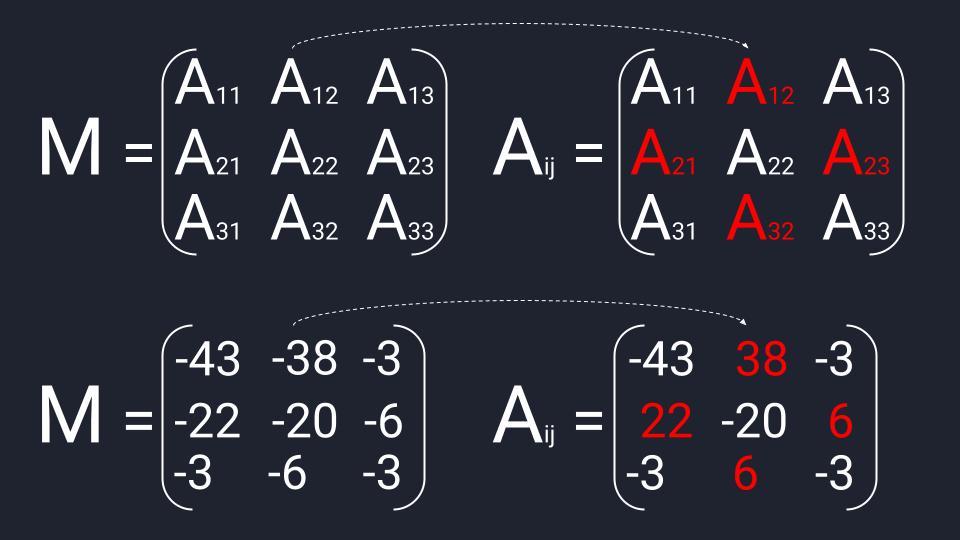
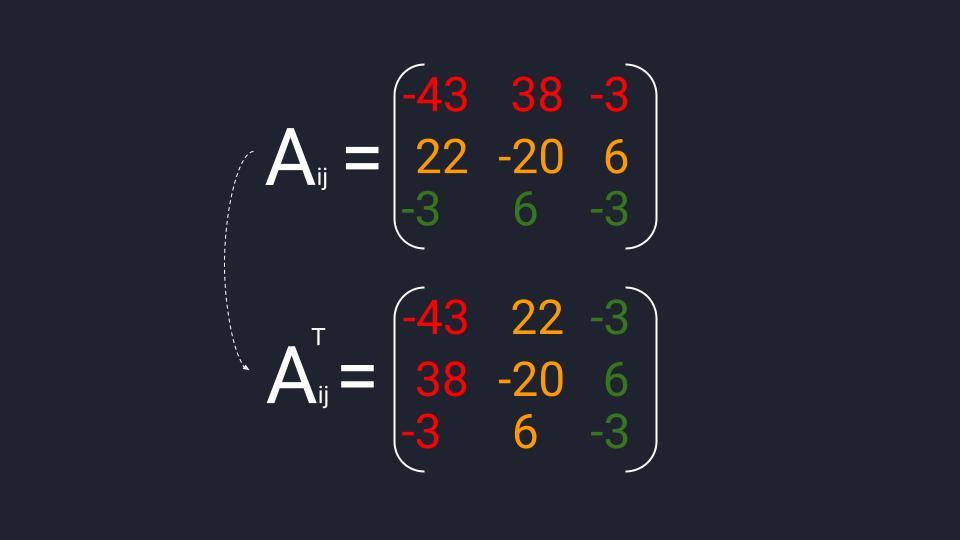
Транспонированная матрица алгебраических дополнений вычисляется в три шага:

Алгоритм вычислений матрицы миноров и матрицы алгебраических дополнений зависит от размера исходной матрицы — чем она больше, тем сложнее формула расчёта. Поэтому мы рассматриваем только матрицы второго и третьего порядка.

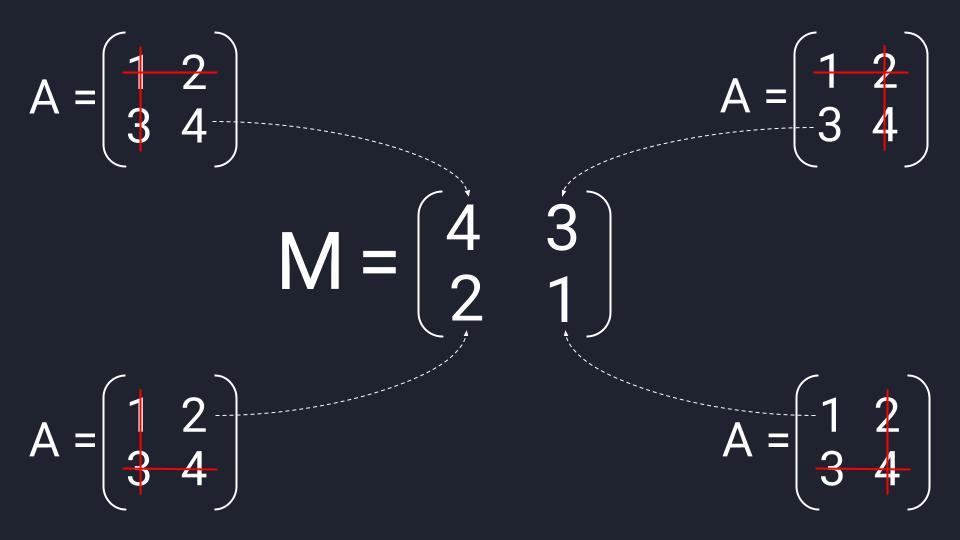
Чтобы найти матрицу миноров второго порядка, нам нужно последовательно зачеркнуть три элемента исходной матрицы:

Когда матрица миноров составлена — меняем знаки элементов второй диагонали и получаем матрицу алгебраических дополнений. Теперь берём эту матрицу и проводим транспонирование — меняем расположение строк и столбцов. Готово.

Пример вычисления матрицы миноров из матрицы второго порядка

Пример вычисления матрицы алгебраических дополнений (Aᵢⱼ ) из матрицы миноров второго порядка

Пример вычисления транспонированной матрицы алгебраических дополнений (Aᵀᵢⱼ), полученной из матрицы миноров второго порядка

Матрица миноров третьего порядка рассчитывается по следующему принципу:

Чтобы не запоминать порядок вычёркивания элементов — попробуйте схему:

После вычёркивания останется квадратная двухразмерная матрица, определитель которой равен разности произведений двух диагоналей.

Пример вычисления первого элемента матрицы миноров из матрицы третьего порядка. Треугольник, или греческая дельта, — это обозначение определителя вне матрицы

Матрицу миноров третьего порядка удобно находить на бумаге с помощью ручки, карандаша и ластика — записываете исходную матрицу, карандашом вычёркиваете линии, считаете определитель, вытираете линии и повторяете процедуру. Рекомендуем попробовать и сверить результат с нашими расчётами.

1-я строка 1-й элемент:

1-я строка 2-й элемент:

1-я строка 3-й элемент:

2-я строка 1-й элемент:

2-я строка 2-й элемент:

2-я строка 3-й элемент:

3-я строка 1-й элемент:

3-я строка 2-й элемент:

3-я строка 3-й элемент:

Считаем матрицу алгебраических дополнений: берём матрицу миноров и меняем на противоположный знак в четырёх элементах — изменяем А₁₂, А₂₁, А₂₃ и А₃₂. Транспонируем полученную матрицу и можем переходить к последнему действию.

Получаем из матрицы третьего порядка матрицу миноров

Меняем знаки в матрице миноров и получаем матрицу алгебраических дополнений (Aᵢⱼ)

Пример вычисления транспонированной матрицы алгебраических дополнений (Aᵀᵢⱼ), полученной из матрицы миноров третьего порядка

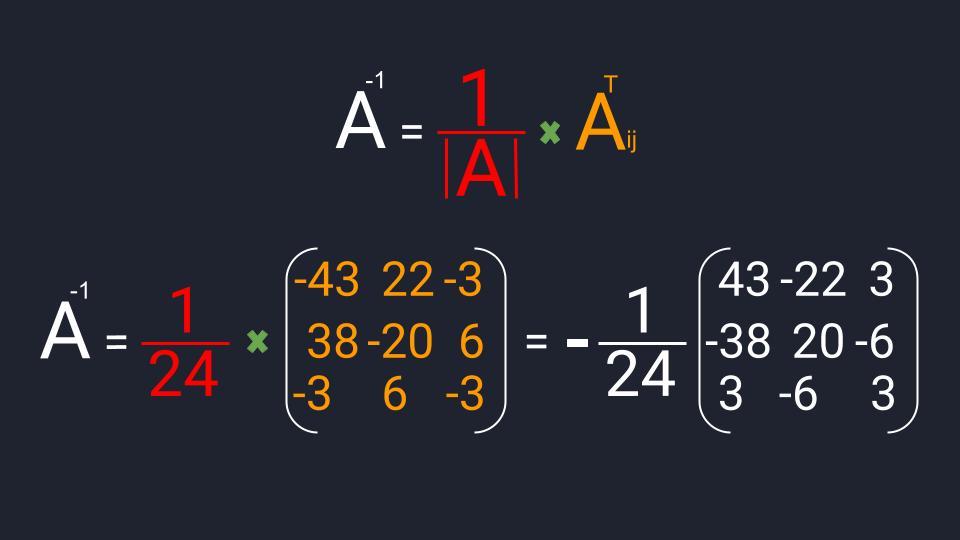
Мы нашли все компоненты для вычисления обратной матрицы. Осталось их подставить в формулу, перемножить и записать ответ:

Пример вычисления обратной матрицы второго порядка: мы внесли дробь в матрицу, но могли этого не делать — просто так захотелось

Пример вычисления обратной матрицы третьего порядка: мы оставили дробь за пределами матрицы и вынесли из матрицы минус. Матрица — это таблица с числами, поэтому не обращайте внимание, если числа получаются большими или неудобными

Господи, зачем всё это?

Мы понимаем, что это всё кажется совершенно оторванным от жизни. Какие-то миноры, детерминанты, о чём вообще речь?

Источник

Как найти обратную матрицу?

Продолжаем разговор о действиях с матрицами. А именно – в ходе изучения данной лекции вы научитесь находить обратную матрицу. Научитесь. Даже если с математикой туго.

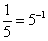
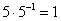
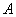
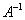
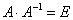
Что такое обратная матрица? Здесь можно провести аналогию с обратными числами: рассмотрим, например, оптимистичное число 5 и обратное ему число . Произведение данных чисел равно единице: . С матрицами всё похоже! Произведение матрицы на обратную ей матрицу равно – единичной матрице, которая является матричным аналогом числовой единицы. Однако обо всём по порядку – сначала решим важный практический вопрос, а именно, научимся эту самую обратную матрицу находить.

Что необходимо знать и уметь для нахождения обратной матрицы? Вы должны уметь решать определители. Вы должны понимать, что такое матрица и уметь выполнять некоторые действия с ними.

Есть? Тогда поехали дальше. А хотя… ехать могут все, если что-то не знаете, я буду ставить нужную ссылку по ходу объяснений.

Существует два основных метода нахождения обратной матрицы:
с помощью алгебраических дополнений и с помощью элементарных преобразований.

Сегодня мы изучим первый, более простой способ.

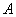
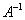
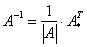
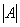
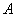
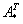
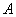
Начнем с самого ужасного и непонятного. Рассмотрим квадратную матрицу . Обратную матрицу можно найти по следующей формуле:

, где – определитель матрицы , – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .

Понятие обратной матрицы существует только для квадратных матриц, матриц «два на два», «три на три» и т.д.

Обозначения: Как вы уже, наверное, заметили, обратная матрица обозначается надстрочным индексом

Начнем с простейшего случая – матрицы «два на два». Чаще всего, конечно, требуется найти обратную матрицу для матрицы «три на три», но, тем не менее, настоятельно рекомендую изучить более простое задание, для того чтобы усвоить общий принцип решения.

Найти обратную матрицу для матрицы

Решаем. Последовательность действий удобно разложить по пунктам.

1) Сначала находим определитель матрицы.

Если с пониманием сего действа плоховато, ознакомьтесь с материалом Как вычислить определитель?

Важно! В том случае, если определитель матрицы равен НУЛЮ – обратной матрицы НЕ СУЩЕСТВУЕТ.

В рассматриваемом примере, как выяснилось, , а значит, всё в порядке.

2) Находим матрицу миноров .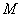

Для решения нашей задачи не обязательно знать, что такое минор, однако, желательно ознакомиться со статьей Как вычислить определитель.

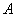
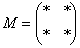
Матрица миноров имеет такие же размеры, как и матрица , то есть в данном случае .
Дело за малым, осталось найти четыре числа и поставить их вместо звездочек.

Возвращаемся к нашей матрице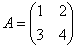
Сначала рассмотрим левый верхний элемент: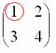

Как найти его минор?
А делается это так: МЫСЛЕННО вычеркиваем строку и столбец, в котором находится данный элемент: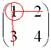

Оставшееся число и является минором данного элемента, которое записываем в нашу матрицу миноров: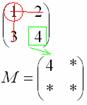

Рассматриваем следующий элемент матрицы :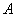

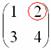
Мысленно вычеркиваем строку и столбец, в котором стоит данный элемент: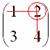

То, что осталось, и есть минор данного элемента, который записываем в нашу матрицу: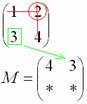

Аналогично рассматриваем элементы второй строки и находим их миноры: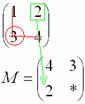


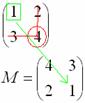
Готово.

– матрица миноров соответствующих элементов матрицы .

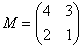
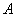
3) Находим матрицу алгебраических дополнений .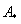

Это просто. В матрице миноров нужно ПОМЕНЯТЬ ЗНАКИ у двух чисел: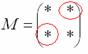

Именно у этих чисел, которые я обвел в кружок!

– матрица алгебраических дополнений соответствующих элементов матрицы .

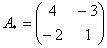
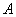
4) Находим транспонированную матрицу алгебраических дополнений .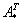

Что такое транспонирование матрицы, и с чем это едят, смотрите в лекции Действия с матрицами.

– транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .

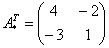
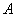
5) Ответ.

Вспоминаем нашу формулу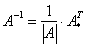
Всё найдено!

Таким образом, обратная матрица:

Ответ лучше оставить в таком виде. НЕ НУЖНО делить каждый элемент матрицы на 2, так как получатся дробные числа. Более подробно данный нюанс рассмотрен в той же статье Действия с матрицами.

Как проверить решение?

Необходимо выполнить матричное умножение 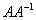либо

Проверка:

Получена уже упомянутая единичная матрица – это матрица с единицами на главной диагонали и нулями в остальных местах.

Таким образом, обратная матрица найдена правильно.

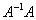
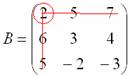
Если провести действие , то в результате тоже получится единичная матрица. Это один из немногих случаев, когда умножение матриц перестановочно, более подробную информацию можно найти в статье Свойства операций над матрицами. Матричные выражения. Также заметьте, что в ходе проверки константа (дробь) выносится вперёд и обрабатывается в самом конце – после матричного умножения. Это стандартный приём.

Переходим к более распространенному на практике случаю – матрице «три на три»:

Найти обратную матрицу для матрицы

Алгоритм точно такой же, как и для случая «два на два».

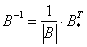
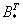
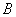
Обратную матрицу найдем по формуле: , где – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .

1) Находим определитель матрицы.

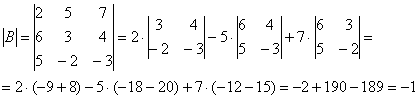
Здесь определитель раскрыт по первой строке.

Также не забываем, что 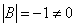, а значит, всё нормально – обратная матрица существует.

2) Находим матрицу миноров .

Матрица миноров имеет размерность «три на три» 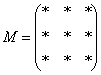, и нам нужно найти девять чисел.

Я подробно рассмотрю парочку миноров:

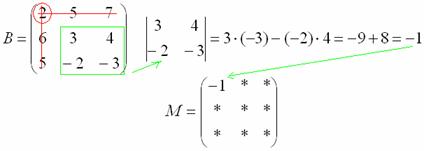
Рассмотрим следующий элемент матрицы: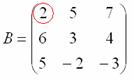

МЫСЛЕННО вычеркиваем строку и столбец, в котором находится данный элемент:

Оставшиеся четыре числа записываем в определитель «два на два»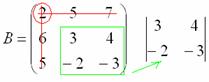

Этот определитель «два на два» и является минором данного элемента. Его нужно вычислить: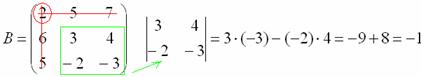

Всё, минор найден, записываем его в нашу матрицу миноров:

Как вы, наверное, догадались, необходимо вычислить девять определителей «два на два». Процесс, конечно, муторный, но случай не самый тяжелый, бывает хуже.

Ну и для закрепления – нахождение еще одного минора в картинках: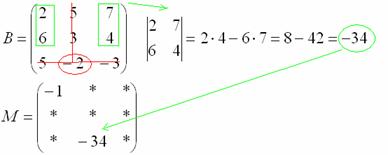

Остальные миноры попробуйте вычислить самостоятельно.

Окончательный результат:
– матрица миноров соответствующих элементов матрицы .

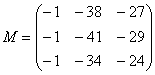
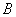
То, что все миноры получились отрицательными – чистая случайность.

3) Находим матрицу алгебраических дополнений .

В матрице миноров необходимо СМЕНИТЬ ЗНАКИ строго у следующих элементов: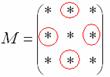

В данном случае:
– матрица алгебраических дополнений соответствующих элементов матрицы .

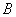
4) Находим транспонированную матрицу алгебраических дополнений .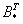

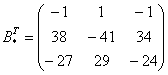
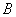
– транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .

5) Ответ:

Проверка:

Таким образом, обратная матрица найдена правильно.

Как оформить решение на чистовик? Примерный образец чистового оформления задания можно найти на странице Правило Крамера. Метод обратной матрицы в параграфе, где идет речь о матричном методе решения системы линейных уравнений. По существу, основная часть упомянутой задачи – и есть поиск обратной матрицы.

Нахождение обратной матрицы для матрицы «четыре на четыре» не рассматриваем, так как такое задание может дать только преподаватель-садист (чтобы студент вычислил один определитель «четыре на четыре» и 16 определителей «три на три»). В моей практике встретился только один такой случай, и заказчик контрольной работы заплатил за мои мучения довольно дорого =).

В ряде учебников, методичек можно встретить несколько другой подход к нахождению обратной матрицы, однако я рекомендую пользоваться именно вышеизложенным алгоритмом решения. Почему? Потому что вероятность запутаться в вычислениях и знаках – гораздо меньше.

Иногда обратную матрицу требуется найти методом Гаусса-Жордана, но второй способ доступен для студентов с приличной техникой элементарных преобразований.

Автор: Емелин Александр

(Переход на главную страницу)

Zaochnik.com – профессиональная помощь студентам

cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5

Tutoronline.ru – онлайн репетиторы по математике и другим предметам

Источник