Как перевести число в тригонометрическую форму

Тригонометрическая форма комплексного числа

Рассмотрим комплексное число, заданной в обычной (алгебраической) форме:

Задача заключается в представлении комплексного числа (1) в тригонометрической форме. Для этого на комплексной плоскости введем полярные координаты. Примем за полюс начало координат, а за полярную ось вещественную ось R.

Как известно, полярными координатами точки z являются длина r ее радиус-вектора, равной расстоянию от точки z до полюса, и величина ее полярного угла, т.е. угла, образованного между полярной осью и вектором-радиусом точки z. Отметим, что направление отсчета угла берется от полярной оси до вектора-радиуса против часовой стрелки (Рис.1, Рис.2).

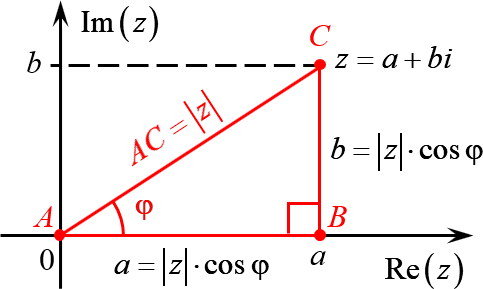
На Рис.3 изображено комплексное число z. Координаты этого числа в декартовой системе координат (a, b). Из определения функций sin и cos любого угла, следует:

Подставляя (2) в (1), получим:

Эта форма записи называется тригонометрической формой записи комплексного числа.

Уравнения (2) возведем в квадрат и сложим:

.

r−длина радиус-вектора комплексного числа z называется модулем комплексного числа и обозначается |z|. Очевидно |z|≥0, причем |z|=0 тогда и только тогда, когда z=0.

Величина полярного угла точки, соответвующей комплексному числу z, т.е. угла φ, называется аргументом этого числа и обозначается arg z. Заметим, что arg z имеет смысл лишь при z≠0. Аргумент комплексного числа 0 не имеет смысла.

Аргумент комплексного числа определен неоднозначно. Если φ аргумент комплексного числа, то φ+2πk, k=0,1. также является аргументом комплексного числа, т.к. cos(φ+2πk)=cosφ, sin(φ+2πk)=sinφ.

Приведение комплексного числа из алгебраической формы в тригонометрическую

Пусть комплексное число представлено в алгебраической форме: z=a+bi. Представим это число в тригонометрической форме. Вычисляем модуль комплексного числа: . Вычисляем аргумент φ комплексного числа из выражений или . Полученные значения вставляем в уравнение (3).

Пример 1. Представить комплексное число z=1 в тригонометрической форме.

Решение. Комплексное число z=1 можно представить так: z=1+0i. Вычислим модуль этого числа: . Вычислим аргумент этого числа: cosφ=1/1. Откуда имеем φ=0. Подставляя значения модуля и аргумента в (3), получим: z=1(cos0+isin0).

Пример 2. Представить комплексное число z=i в тригонометрической форме.

Решение. Комплексное число z=i можно представить так: z=0+1i. Вычислим модуль этого числа: . Вычислим аргумент этого числа: cosφ=0/1. Откуда имеем φ=π/2. Подставляя значения модуля и аргумента в (3), получим: .

Ответ. .

Пример 3. Представить комплексное число z=4+3i в тригонометрической форме.

Решение. Вычислим модуль этого числа: . Вычислим аргумент этого числа: cosφ=4/5. Откуда имеем φ=arccos(4/5). Подставляя значения модуля и аргумента в (3), получим: .

Ответ. , где φ=arccos(4/5).

Умножение комплексных чисел в тригонометрической форме записи

В результате умножения комплексных чисел в тригонометрической форме мы получили комплексное число в тригонометрической форме, следовательно |z₁z₂|=r₁r₂, или

Пример 4. Умножить комплексные числа и .

Решение. Воспользуемся формулой (5):

Ответ. .

Деление комплексных чисел в тригонометрической форме записи

Отсюда следует, что или

Далее , или

Пример 5. Делить комплексные числа и .

Решение. Воспользуемся формулой (8):

Ответ. .

Источник

Тригонометрическая форма комплексных чисел

Второй урок по комплексным числам. Если вы только начинаете изучать эту тему (что такое комплексная единица, модуль, сопряжённые), см. первый урок: «Что такое комплексное число».

Начнём с ключевого определения.

1. Тригонометрическая форма

Определение. Тригонометрическая форма комплексного числа — это выражение вида

\[z=\left| z \right|\cdot \left( \cos \text< >\!\!\varphi\!\!\text< >+i\sin \text< >\!\!\varphi\!\!\text < >\right)\]

Выносим модуль за скобки:

\[z=\sqrt<3>+1\cdot i=2\cdot \left( \frac<\sqrt<3>><2>+\frac<1><2>\cdot i \right)\]

Вспоминаем тригонометрию, 10-й класс:

2. Умножение и деление комплексных чисел

Комплексные числа, записанные в тригонометрической форме, очень удобно умножать и делить.

Теорема. Пусть даны два комплексных числа:

\[\begin & <_<1>>=\left| <_<1>> \right|\cdot \left( \cos \alpha +i\sin \alpha \right) \\ & <_<2>>=\left| <_<2>> \right|\cdot \left( \cos \beta +i\sin \beta \right) \\ \end\]

Тогда их произведение равно

\[<_<1>>\cdot <_<2>>=\left| <_<1>> \right|\cdot \left| <_<2>> \right|\cdot \left( \cos \left( \alpha +\beta \right)+i\sin \left( \alpha +\beta \right) \right)\]

Получается, что при умножении комплексных чисел мы просто умножаем их модули, а аргументы складываем. При делении — делим модули и вычитаем аргументы. И всё!

Найти произведение и частное двух комплексных чисел:

\[\begin <_<1>>\cdot <_<2>> & =2\cdot 5\cdot \left( \cos \left( \frac<\pi ><3>+\frac<\pi > <6>\right)+i\sin \left( \frac<\pi ><3>+\frac<\pi > <6>\right) \right)= \\ & =10\cdot \left( \cos \frac<\pi ><2>+i\sin \frac<\pi > <2>\right) \\ \end\]

\[\begin \frac<<_<1>>><<_<2>>> & =\frac<2><5>\cdot \left( \cos \left( \frac<\pi ><3>-\frac<\pi > <6>\right)+i\sin \left( \frac<\pi ><3>-\frac<\pi > <6>\right) \right)= \\ & =0,4\cdot \left( \cos \frac<\pi ><6>+i\sin \frac<\pi > <6>\right) \\ \end\]

По сравнению со стандартной (алгебраической) формой записи комплексных чисел экономия сил и времени налицо.:)

3. Формула Муавра

Пусть дано комплексное число в тригонометрической форме:

\[z=\left| z \right|\cdot \left( \cos \text< >\!\!\varphi\!\!\text< >+i\sin \text< >\!\!\varphi\!\!\text < >\right)\]

Возведём его в квадрат, умножив на само себя:

\[\begin <^<2>> & =z\cdot z = \\ & =\left| z \right|\left| z \right|\cdot \left( \cos \left( \text< >\!\!\varphi\!\!\text< + >\!\!\varphi\!\!\text < >\right)+i\sin \left( \text< >\!\!\varphi\!\!\text< + >\!\!\varphi\!\!\text < >\right) \right)= \\ & =<<\left| z \right|>^<2>>\cdot \left( \cos 2\text< >\!\!\varphi\!\!\text< >+i\sin 2\text< >\!\!\varphi\!\!\text < >\right) \\ \end\]

Затем возведём в куб, умножив на себя ещё раз:

Формула Муавра. При возведении всякого комплексного числа

\[z=\left| z \right|\cdot \left( \cos \varphi +i\sin \varphi \right)\]

Представим первое число в тригонометрической форме:

Последним шагом мы воспользовались периодичностью синуса и косинуса, уменьшив аргумент сразу на 28π.

Следующую задачу в разных вариациях любят давать на контрольных работах и экзаменах:

Теперь второе число запишем в комплексной форме:

Вот так всё просто! Следующие два раздела предназначены для углублённого изучения. Для тех, кто хочет действительно разобраться в комплексных числах.

4. Дополнение 1. Геометрический подход

А теперь объединим эти картинки и попробуем перейти из декартовой системы координат в полярную:

\[\begin & AB=AC\cdot \cos \varphi =\left| z \right|\cdot \cos \varphi \\ & BC=AC\cdot \sin \varphi =\left| z \right|\cdot \sin \varphi \\ \end\]

\[\begin a+bi & =\left| z \right|\cos \varphi +i\cdot \left| z \right|\sin \varphi = \\ & =\left| z \right|\left( \cos \varphi +i\sin \varphi \right) \\ \end\]

Такой угол обязательно найдётся, поскольку выполняется основное тригонометрическое тождество:

На практике основная трудность заключается именно в поиске подходящего аргумента.

5. Дополнение 2. Как найти аргумент?

В учебниках пишут много разной дичи, типа вот этой:

Формула правильная, но пользы от неё — ноль. Запомнить сложно, а применять и вовсе невозможно. Мы пойдём другим путём.

5.1. Точки на координатных осях

Для начала рассмотрим точки, лежащие осях координат.

5.2. Точки с арктангенсом

Очевидно, это острый угол:

В правой полуплоскости мы откладываем от «нулевого» луча:

\[\begin 3+4i & =5\cdot \left( \cos \varphi +i\sin \varphi \right) \\ \varphi & =\operatorname\frac<4> <3>\end\]

\[\begin -5-3i & =\sqrt<34>\cdot \left( \cos \varphi +i\sin \varphi \right) \\ \varphi & =\pi +\operatorname\frac<3> <5>\end\]

Звучит просто, выглядит красиво, работает идеально! Но требует небольшой практики. Пробуйте, тренируйтесь и берите на вооружение.

А в следующем уроке мы научимся извлекать корни из комплексных чисел.:)

Источник

Алгебра и начала математического анализа. 11 класс

Конспект урока

Алгебра и начала математического анализа, 11 класс

Урок №40. Тригонометрическая форма комплексного числа.

Перечень вопросов, рассматриваемых в теме

1) понятие модуля комплексного числа;

2) понятие тригонометрической формы комплексного числа;

3) перевод комплексного числа в тригонометрическую форму.

Модулем комплексного числа z называется расстояние от начала координат до соответствующей точки комплексной плоскости. Попросту говоря, модуль – это длина радиус-вектора, который на чертеже обозначен красным цветом.

Аргументом комплексного числа z называется угол φ между положительной полуосью действительной оси Re z и радиус-вектором, проведенным из начала координат к соответствующей точке. Аргумент не определён для единственного числа: z=0.

Для этого рассмотрим формулы для нахождения в зависимости от а и b.

1.

2.

3.

4.

5.

6.

7.

8.

Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., Учебник комплект под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл.– М.: Просвещение, 2014.

Шабунин М.И., Ткачева М.В., Федорова Н.Е.Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл.– М.: Просвещение, 2017.

Теоретический материал для самостоятельного изучения

Но в электротехнике, электрооборудовании, электронике, автоматике и других дисциплинах комплексное число записывается в тригонометрической форме.

Тригонометрическая форма комплексного числа r(cos φ+sin φ).

На любом трансформаторе стоит маркировка cos φ=. Это энергетический показатель ГОС стандартов. Он показывает эффективность работы, КПД, cos φ- активный показатель мощности, тока, напряжения. sin φ- реактивный показатель.

Любое комплексное число (кроме нуля) z=a+bi можно записать в тригонометрической форме: z=|z|∙(cosφ+isinφ), где |z| – это модуль комплексного числа, а φ – аргумент комплексного числа.

Модулем комплексного числа z называется расстояние от начала координат до соответствующей точки комплексной плоскости. Попросту говоря, модуль – это длина радиус-вектора, который на чертеже обозначен красным цветом.

Модуль комплексного числа z стандартно обозначают: |z| или r.

По теореме Пифагора легко вывести формулу для нахождения модуля комплексного числа: . Данная формула справедлива для любых значений a и b.

Аргументом комплексного числа z называется угол φ между положительной полуосью действительной оси Re z и радиус-вектором, проведенным из начала координат к соответствующей точке. Аргумент не определён для единственного числа: z=0.

Аргумент комплексного числа z стандартно обозначают: φ или arg z.

Из геометрических соображений получается следующая формула для нахождения аргумента:

Внимание! Данная формула работает только в правой полуплоскости! Если комплексное число располагается не в 1-ой и не 4-ой координатной четверти, то формула будет немного другой.

Для этого рассмотрим формулы для нахождения в зависимости от а и b.

1.

2.

3.

4.

5.

6.

7.

8.

Поскольку a 0, то – вот здесь нечетностью арктангенса воспользоваться нужно. К сожалению, в таблице отсутствует значение arctg 2, поэтому в подобных случаях аргумент приходится оставлять в громоздком виде:

— число z в тригонометрической форме.

Разбор решения заданий тренировочного модуля

№1. Тип задания: единичный выбор

Найдем его модуль и аргумент.

Поскольку a 0, то – вот здесь нечетностью арктангенса воспользоваться нужно. К сожалению, в таблице отсутствует значение arctg 2, поэтому в подобных случаях аргумент приходится оставлять в громоздком виде:

— число z в тригонометрической форме.

Значит, верный ответ 1

№2. Тип задания: ввод с клавиатуры пропущенных элементов в тексте.

Найдите куб суммы z= (3+4i) 3 =_____________

Возведем данное выражение в третью степень

Упрощаем полученное выражение, учитывая, что i 2 =-1

Ответ:

Источник