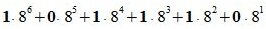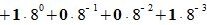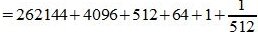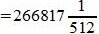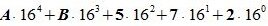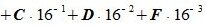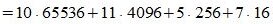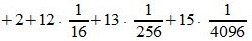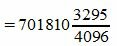Как перевести число в десятичную систему
Перевод из любой системы счисления в десятичную
Перевести любое число позиционной системы счисления в десятичное достаточно просто, для этого необходимо воспользоваться формулой. Важное замечание состоит в том, что для перевода целого и дробного q-ичного числа используются разные, хоть и схожие, формулы.
Таблица соответствия популярных систем счисления
Перед тем как перейти к алгоритму перевода, вспомним таблицу соответствия:
| Десятичная система | Двоичная система | Восьмеричная система | Шестнадцатеричная система |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 2 | 10 | 2 | 2 |
| 3 | 11 | 3 | 3 |
| 4 | 100 | 4 | 4 |
| 5 | 101 | 5 | 5 |
| 6 | 110 | 6 | 6 |
| 7 | 111 | 7 | 7 |
| 8 | 1000 | 10 | 8 |
| 9 | 1001 | 11 | 9 |
| 10 | 1010 | 12 | A |
| 11 | 1011 | 13 | B |
| 12 | 1100 | 14 | C |
| 13 | 1101 | 15 | D |
| 14 | 1110 | 16 | E |
| 15 | 1111 | 17 | F |
Алгоритм перевода целого q-ичного числа в десятичную систему счисления
Для перевода целого числа с основанием q в десятичное, обратимся к развернутой форме записи числа для позиционной системы счисления:
где A — число, q — основание системы счисления, а n — количество разрядов числа.
Пример 1: Перевести число 10011 из двоичной системы в десятичную
Применив развернутую форму записи числа, получим:
100112=1 ∙ 2 4 + 0 ∙ 2 3 + 0 ∙ 2 2 + 1 ∙ 2 1 + 1 ∙ 2 0 = 1 ∙ 16 + 0 ∙ 8 + 0 ∙ 4 + 1 ∙ 2 + 1 ∙ 1 = 16 + 0 + 0 + 2 + 1 = 1910
Пример 2: Перевести число 17 из восьмеричной системы в десятичную
Аналогично предыдущему примеру, применив развернутую форму записи числа, получим:
178=1 ∙ 8 1 + 7 ∙ 8 0 = 1 ∙ 8 + 7 ∙ 1 = 8 + 7 = 1510
Ответ можно сравнить с таблицей соответствия и убедиться, что 178 = 1510.
Пример 3: Перевести число 20341 из пятеричной системы в десятичную
203415=2 ∙ 5 4 + 0 ∙ 5 3 + 3 ∙ 5 2 + 4 ∙ 5 1 + 1 ∙ 5 0 = 2 ∙ 625 + 0 ∙ 125 + 3 ∙ 25 + 4 ∙ 5 + 1 ∙ 1 = 1250 + 0 + 75 + 20 + 1 = 134610
Алгоритм перевода q-ичной дроби в десятичную систему счисления
Как и в предыдущем случае, для перевода q-ичной дроби в десятичную систему, воспользуемся развернутой формой представления дробей в позиционных системах:
где A — число, q — основание системы счисления, n — количество целых разрядов, а m — количество дробных разрядов числа.
Пример 4: Перевести число 0,F3D0 из шестнадцатеричной системы в десятичную
Применив развернутую форму записи дробного числа, получим:
Ответ: 0.F3D016 = 0.95239257812510
Перевод чисел из одной системы счисления в другую
Данный конвертер переводит числа между наиболее популярными системами счисления: десятичной, двоичной, восьмеричной, шестнадцатеричной.
Существуют и другие системы счисления, но мы не стали включать их в конвертер из-за низкой популярности.
Для указания системы счисления при записи числа используется нижний индекс, который ставится после числа:
20010 = 110010002 = 3108 = C816
Кратко об основных системах счисления
Десятичная система счисления. Используется в повседневной жизни и является самой распространенной. Все числа, которые нас окружают представлены в этой системе. В каждом разряде такого числа может использоваться только одна цифра от 0 до 9.
Двоичная система счисления. Используется в вычислительной технике. Для записи числа используются цифры 0 и 1.
Восьмеричная система счисления. Также иногда применяется в цифровой технике. Для записи числа используются цифры от 0 до 7.
Перевод в десятичную систему счисления
Перевод из десятичной системы счисления в другие
Делим десятичное число на основание системы, в которую хотим перевести и записываем остатки от деления. Запишем полученные остатки в обратном порядке и получим искомое число.
Переведем число 37510 в восьмеричную систему:
Перевод из двоичной системы в восьмеричную
Так же как и в первом способе разбиваем число на группы. Но вместо преобразований в скобках просто заменим полученные группы (триады) на соответствующие цифры восьмеричной системы, используя таблицу триад:
Перевод из двоичной системы в шестнадцатеричную
Также как и в первом способе разбиваем число на группы по 4 цифры. Заменим полученные группы (тетрады) на соответствующие цифры шестнадцатеричной системы, используя таблицу тетрад:
| Тетрада | 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Цифра | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
Перевод из восьмеричной системы в двоичную
Каждый разряд восьмеричного числа будем делить на 2 и записывать остатки в обратном порядке, формируя группы по 3 разряда двоичного числа. Если в группе получилось меньше 3 разрядов, тогда дополняем нулями. Записываем все группы по порядку, отбрасываем ведущие нули, если имеются, и получаем двоичное число.
Используем таблицу триад:
Каждую цифру исходного восьмеричного числа заменяется на соответствующие триады. Ведущие нули самой первой триады отбрасываются.
Перевод из шестнадцатеричной системы в двоичную
Аналогично переводу из восьмеричной в двоичную, только группы по 4 разряда.
Используем таблицу тетрад:
| Цифра | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Тетрада | 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
Каждую цифру исходного числа заменяется на соответствующие тетрады. Ведущие нули самой первой тетрады отбрасываются.
Перевод из восьмеричной системы в шестнадцатеричную и наоборот
Такую конвертацию можно осуществить через промежуточное десятичное или двоичное число. То есть исходное число сначала перевести в десятичное (или двоичное), и затем полученный результат перевести в конечную систему счисления.
Перевод чисел из одной системы счисления в другую онлайн
С помощю этого онлайн калькулятора можно перевести целые и дробные числа из одной системы счисления в другую. Дается подробное решение с пояснениями. Для перевода введите исходное число, задайте основание сисемы счисления исходного числа, задайте основание системы счисления, в которую нужно перевести число и нажмите на кнопку «Перевести». Теоретическую часть и численные примеры смотрите ниже.
Предупреждение
Перевод целых и дробных чисел из одной системы счисления в любую другую − теория, примеры и решения
Существуют позиционные и не позиционные системы счисления. Арабская система счисления, которым мы пользуемся в повседневной жизни, является позиционной, а римская − нет. В позиционных системах счисления позиция числа однозначно определяет величину числа. Рассмотрим это на примере числа 6372 в десятичном системе счисления. Пронумеруем это число справа налево начиная с нуля:
| число | 6 | 3 | 7 | 2 |
| позиция | 3 | 2 | 1 | 0 |
Тогда число 6372 можно представить в следующем виде:
Число 10 определяет систему счисления (в данном случае это 10). В качестве степеней взяты значения позиции данного числа.
Рассмотрим вещественное десятичное число 1287.923. Пронумеруем его начиная с нуля позиции числа от десятичной точки влево и вправо:
| число | 1 | 2 | 8 | 7 | . | 9 | 2 | 3 |
| позиция | 3 | 2 | 1 | 0 | -1 | -2 | -3 |
Тогда число 1287.923 можно представить в виде:
В общем случае формулу можно представить в следующем виде:
В таблице Таб.1 представлены числа в разных системах счисления.
| Таблица 1 | |||
|---|---|---|---|
| Система счисления | |||
| 10 | 2 | 8 | 16 |
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 2 | 10 | 2 | 2 |
| 3 | 11 | 3 | 3 |
| 4 | 100 | 4 | 4 |
| 5 | 101 | 5 | 5 |
| 6 | 110 | 6 | 6 |
| 7 | 111 | 7 | 7 |
| 8 | 1000 | 10 | 8 |
| 9 | 1001 | 11 | 9 |
| 10 | 1010 | 12 | A |
| 11 | 1011 | 13 | B |
| 12 | 1100 | 14 | C |
| 13 | 1101 | 15 | D |
| 14 | 1110 | 16 | E |
| 15 | 1111 | 17 | F |
Перевод чисел из одной системы счисления в другую
Для перевода чисел с одной системы счисления в другую, проще всего сначала перевести число в десятичную систему счисления, а затем, из десятичной системы счисления перевести в требуемую систему счисления.
Перевод чисел из любой системы счисления в десятичную систему счисления
С помощью формулы (1) можно перевести числа из любой системы счисления в десятичную систему счисления.
Пример 1. Переводить число 1011101.001 из двоичной системы счисления (СС) в десятичную СС. Решение:
Пример 2. Переводить число 1011101.001 из восьмеричной системы счисления (СС) в десятичную СС. Решение:
Пример 3. Переводить число AB572.CDF из шестнадцатеричной системы счисления в десятичную СС. Решение:
Перевод чисел из десятичной системы счисления в другую систему счисления
Для перевода чисел из десятичной системы счисления в другую систему счисления нужно переводить отдельно целую часть числа и дробную часть числа.
Пример 4. Переведем число 159 из десятичной СС в двоичную СС:
| 159 | 2 | ||
| 158 | 79 | 2 | |
| 1 | 78 | 39 | 2 |
| 1 | 38 | 19 | 2 |
| 1 | 18 | 9 | 2 |
| 1 | 8 | 4 | 2 |
| 1 | 4 | 2 | 2 |
| 0 | 2 | 1 | |
| 0 |
Как видно из Рис. 1, число 159 при делении на 2 дает частное 79 и остаток 1. Далее число 79 при делении на 2 дает частное 39 и остаток 1 и т.д. В результате построив число из остатков деления (справа налево) получим число в двоичной СС: 10011111. Следовательно можно записать:
Пример 5. Переведем число 615 из десятичной СС в восьмеричную СС.
| 615 | 8 | ||
| 608 | 76 | 8 | |
| 7 | 72 | 9 | 8 |
| 4 | 8 | 1 | |
| 1 |
При приведении числа из десятичной СС в восьмеричную СС, нужно последовательно делить число на 8, пока не получится целый остаток меньшее, чем 8. В результате построив число из остатков деления (справа налево) получим число в восьмеричной СС: 1147(см. Рис. 2). Следовательно можно записать:
Пример 6. Переведем число 19673 из десятичной системы счисления в шестнадцатеричную СС.
| 19673 | 16 | ||
| 19664 | 1229 | 16 | |
| 9 | 1216 | 76 | 16 |
| 13 | 64 | 4 | |
| 12 |
Далее рассмотрим перевод правильных десятичных дробей в двоичную СС, в восьмеричную СС, в шестнадцатеричную СС и т.д.
Для перевода правильных десятичных дробей (вещественное число с нулевой целой частью) в систему счисления с основанием s необходимо данное число последовательно умножить на s до тех пор, пока в дробной части не получится чистый нуль, или же не получим требуемое количество разрядов. Если при умножении получится число с целой частью, отличное от нуля, то эту целую часть не учитывать (они последовательно зачисливаются в результат).
Рассмотрим вышеизложенное на примерах.
Пример 7. Переведем число 0.214 из десятичной системы счисления в двоичную СС.
| 0.214 | |
| x | 2 |
| 0 | 0.428 |
| x | 2 |
| 0 | 0.856 |
| x | 2 |
| 1 | 0.712 |
| x | 2 |
| 1 | 0.424 |
| x | 2 |
| 0 | 0.848 |
| x | 2 |
| 1 | 0.696 |
| x | 2 |
| 1 | 0.392 |
Как видно из Рис.4, число 0.214 последовательно умножается на 2. Если в результате умножения получится число с целой частью, отличное от нуля, то целая часть записывается отдельно (слева от числа), а число записывается с нулевой целой частью. Если же при умножении получиться число с нулевой целой частью, то слева от нее записывается нуль. Процесс умножения продолжается до тех пор, пока в дробной части не получится чистый нуль или же не получим требуемое количество разрядов. Записывая жирные числа (Рис.4) сверху вниз получим требуемое число в двоичной системе счисления: 0. 0011011.
Следовательно можно записать:
Пример 8. Переведем число 0.125 из десятичной системы счисления в двоичную СС.
| 0.125 | |
| x | 2 |
| 0 | 0.25 |
| x | 2 |
| 0 | 0.5 |
| x | 2 |
| 1 | 0.0 |
Для приведения числа 0.125 из десятичной СС в двоичную, данное число последовательно умножается на 2. В третьем этапе получилось 0. Следовательно, получился следующий результат:
Пример 9. Переведем число 0.214 из десятичной системы счисления в шестнадцатеричную СС.
| 0.214 | |
| x | 16 |
| 3 | 0.424 |
| x | 16 |
| 6 | 0.784 |
| x | 16 |
| 12 | 0.544 |
| x | 16 |
| 8 | 0.704 |
| x | 16 |
| 11 | 0.264 |
| x | 16 |
| 4 | 0.224 |
Следуя примерам 4 и 5 получаем числа 3, 6, 12, 8, 11, 4. Но в шестнадцатеричной СС числам 12 и 11 соответствуют числа C и B. Следовательно имеем:
Пример 10. Переведем число 0.512 из десятичной системы счисления в восьмеричную СС.
| 0.512 | |
| x | 8 |
| 4 | 0.096 |
| x | 8 |
| 0 | 0.768 |
| x | 8 |
| 6 | 0.144 |
| x | 8 |
| 1 | 0.152 |
| x | 8 |
| 1 | 0.216 |
| x | 8 |
| 1 | 0.728 |
Пример 11. Переведем число 159.125 из десятичной системы счисления в двоичную СС. Для этого переведем отдельно целую часть числа (Пример 4) и дробную часть числа (Пример 8). Далее объединяя эти результаты получим:
Пример 12. Переведем число 19673.214 из десятичной системы счисления в шестнадцатеричную СС. Для этого переведем отдельно целую часть числа (Пример 6) и дробную часть числа (Пример 9). Далее объединяя эти результаты получим:
Способы перевода чисел из одной системы счисления в другую
Сдающим ЕГЭ и не только…
Странно, что в школах на уроках информатики обычно показывают ученикам самый сложный и неудобный способ перевода чисел из одной системы в другую. Это способ заключается в последовательном делении исходного числа на основание и сборе остатков от деления в обратном порядке.
Например, нужно перевести число 81010 в двоичную систему:

Результат записываем в обратном порядке снизу вверх. Получается 81010 = 11001010102
Если нужно переводить в двоичную систему довольно большие числа, то лестница делений приобретает размер многоэтажного дома. И как тут собрать все единички с нулями и ни одной не пропустить?
В программу ЕГЭ по информатике входят несколько задач, связанных с переводом чисел из одной системы в другую. Как правило, это преобразование между 8- и 16-ричными системами и двоичной. Это разделы А1, В11. Но есть и задачи с другими системами счисления, как например, в разделе B7.
Для начала напомним две таблицы, которые хорошо бы знать наизусть тем, кто выбирает информатику своей дальнейшей профессией.
Таблица степеней числа 2:
| 2 1 | 2 2 | 2 3 | 2 4 | 2 5 | 2 6 | 2 7 | 2 8 | 2 9 | 2 10 |
| 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1024 |
Она легко получается умножением предыдущего числа на 2. Так, что если помните не все эти числа, остальные нетрудно получить в уме из тех, которые помните.
Таблица двоичных чисел от 0 до 15 c 16-ричным представлением:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
Недостающие значения тоже нетрудно вычислить, прибавляя по 1 к известным значениям.
Перевод целых чисел
Итак, начнем с перевода сразу в двоичную систему. Возьмём то же число 81010. Нам нужно разложить это число на слагаемые, равные степеням двойки.
Способ 2: Распишем слагаемые как степени двойки друг под другом, начиная с большего.
Вот и всё. Попутно также просто решается задача «сколько единиц в двоичной записи числа 810?».
Ответ — столько, сколько слагаемых (степеней двойки) в таком его представлении. У 810 их 5.
Теперь пример попроще.
Ну и, наконец, совсем лёгкие переводы между 8- и 16-ричными системами. Так как их основанием является степень двойки, то перевод делается автоматически, просто заменой цифр на их двоичное представление. Для 8-ричной системы каждая цифра заменяется тремя двоичными разрядами, а для 16-ричной четырьмя. При этом все ведущие нули обязательны, кроме самого старшего разряда.
Переведем в двоичную систему число 5478.
| 5478= | 101 | 100 | 111 |
| 5 | 4 | 7 |
Ещё одно, например 7D6A16.
| 7D6A16= | (0)111 | 1101 | 0110 | 1010 |
| 7 | D | 6 | A |
Перевод отрицательных чисел
Здесь нужно учесть, что число будет представлено в дополнительном коде. Для перевода числа в дополнительный код нужно знать конечный размер числа, то есть во что мы хотим его вписать — в байт, в два байта, в четыре. Старший разряд числа означает знак. Если там 0, то число положительное, если 1, то отрицательное. Слева число дополняется знаковым разрядом. Беззнаковые (unsigned) числа мы не рассматриваем, они всегда положительные, а старший разряд в них используется как информационный.
Для перевода отрицательного числа в двоичный дополнительный код нужно перевести положительное число в двоичную систему, потом поменять нули на единицы и единицы на нули. Затем прибавить к результату 1.
Перевод дробных чисел
Дробные числа переводятся способом, обратным делению целых чисел на основание, который мы рассмотрели в самом начале. То есть при помощи последовательного умножения на новое основание с собиранием целых частей. Полученные при умножении целые части собираются, но не участвуют в следующих операциях. Умножаются только дробные. Если исходное число больше 1, то целая и дробная части переводятся отдельно, потом склеиваются.
Переведем число 0,6752 в двоичную систему.
| 0 | ,6752 |
| *2 | |
| 1 | ,3504 |
| *2 | |
| 0 | ,7008 |
| *2 | |
| 1 | ,4016 |
| *2 | |
| 0 | ,8032 |
| *2 | |
| 1 | ,6064 |
| *2 | |
| 1 | ,2128 |
Процесс можно продолжать долго, пока не получим все нули в дробной части или будет достигнута требуемая точность. Остановимся пока на 6-м знаке.
Системы счисления. Перевод из одной системы в другую.
1. Порядковый счет в различных системах счисления.
В современной жизни мы используем позиционные системы счисления, то есть системы, в которых число, обозначаемое цифрой, зависит от положения цифры в записи числа. Поэтому в дальнейшем мы будем говорить только о них, опуская термин «позиционные».
Для того чтобы научиться переводить числа из одной системы в другую, поймем, как происходит последовательная запись чисел на примере десятичной системы.
Поскольку у нас десятичная система счисления, мы имеем 10 символов (цифр) для построения чисел. Начинаем порядковый счет: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Цифры закончились. Мы увеличиваем разрядность числа и обнуляем младший разряд: 10. Затем опять увеличиваем младший разряд, пока не закончатся все цифры: 11, 12, 13, 14, 15, 16, 17, 18, 19. Увеличиваем старший разряд на 1 и обнуляем младший: 20. Когда мы используем все цифры для обоих разрядов (получим число 99), опять увеличиваем разрядность числа и обнуляем имеющиеся разряды: 100. И так далее.
Попробуем сделать то же самое в 2-ной, 3-ной и 5-ной системах (введем обозначение для 2-ной системы, для 3-ной и т.д.):
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 2 | 10 | 2 | 2 |
| 3 | 11 | 10 | 3 |
| 4 | 100 | 11 | 4 |
| 5 | 101 | 12 | 10 |
| 6 | 110 | 20 | 11 |
| 7 | 111 | 21 | 12 |
| 8 | 1000 | 22 | 13 |
| 9 | 1001 | 100 | 14 |
| 10 | 1010 | 101 | 20 |
| 11 | 1011 | 102 | 21 |
| 12 | 1100 | 110 | 22 |
| 13 | 1101 | 111 | 23 |
| 14 | 1110 | 112 | 24 |
| 15 | 1111 | 120 | 30 |
Если система счисления имеет основание больше 10, то нам придется вводить дополнительные символы, принято вводить буквы латинского алфавита. Например, для 12-ричной системы кроме десяти цифр нам понадобятся две буквы ( и ):
| 0 | 0 |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | 5 |
| 6 | 6 |
| 7 | 7 |
| 8 | 8 |
| 9 | 9 |
| 10 | |
| 11 | |
| 12 | 10 |
| 13 | 11 |
| 14 | 12 |
| 15 | 13 |
2.Перевод из десятичной системы счисления в любую другую.
Чтобы перевести целое положительное десятичное число в систему счисления с другим основанием, нужно это число разделить на основание. Полученное частное снова разделить на основание, и дальше до тех пор, пока частное не окажется меньше основания. В результате записать в одну строку последнее частное и все остатки, начиная с последнего.
Пример 1. Переведем десятичное число 46 в двоичную систему счисления.
Пример 2. Переведем десятичное число 672 в восьмеричную систему счисления.
Пример 3. Переведем десятичное число 934 в шестнадцатеричную систему счисления.
3. Перевод из любой системы счисления в десятичную.
Для того, чтобы научиться переводить числа из любой другой системы в десятичную, проанализируем привычную нам запись десятичного числа.
Например, десятичное число 325 – это 5 единиц, 2 десятка и 3 сотни, т.е.
Точно так же обстоит дело и в других системах счисления, только умножать будем не на 10, 100 и пр., а на степени основания системы счисления. Для примера возьмем число 1201 в троичной системе счисления. Пронумеруем разряды справа налево начиная с нуля и представим наше число как сумму произведений цифры на тройку в степени разряда числа:
Это и есть десятичная запись нашего числа, т.е.
Пример 4. Переведем в десятичную систему счисления восьмеричное число 511.
Пример 5. Переведем в десятичную систему счисления шестнадцатеричное число 1151.
4. Перевод из двоичной системы в систему с основанием «степень двойки» (4, 8, 16 и т.д.).
Для преобразования двоичного числа в число с основанием «степень двойки» необходимо двоичную последовательность разбить на группы по количеству цифр равному степени справа налево и каждую группу заменить соответствующей цифрой новой системы счисления.
Например, Переведем двоичное 1100001111010110 число в восьмеричную систему. Для этого разобьем его на группы по 3 символа начиная справа (т.к. ), а затем воспользуемся таблицей соответствия и заменим каждую группу на новую цифру:
Таблицу соответствия мы научились строить в п.1.
| 0 | 0 |
| 1 | 1 |
| 10 | 2 |
| 11 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
Пример 6. Переведем двоичное 1100001111010110 число в шестнадцатеричную систему.
| 0 | 0 |
| 1 | 1 |
| 10 | 2 |
| 11 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
| 1000 | 8 |
| 1001 | 9 |
| 1010 | A |
| 1011 | B |
| 1100 | C |
| 1101 | D |
| 1110 | E |
| 1111 | F |
5.Перевод из системы с основанием «степень двойки» (4, 8, 16 и т.д.) в двоичную.
Этот перевод аналогичен предыдущему, выполненному в обратную сторону: каждую цифру мы заменяем группой цифр в двоичной системе из таблицы соответствия.
Пример 7. Переведем шестнадцатеричное число С3A6 в двоичную систему счисления.
Для этого каждую цифру числа заменим группой из 4 цифр (т.к. ) из таблицы соответствия, дополнив при необходимости группу нулями вначале: