Как перевести число неправильную дробь
Перевод смешанного или целого числа в неправильную дробь
Общие сведения о дробях
Дробь — форма записи рационального числа в виде доли целого.
В стандартном виде дроби записываются так: \( \frac mn.\)
Число над чертой называется числителем, под ней — знаменателем. Такую запись можно передать словами, как m частей из n, причем \(\frac nn\) равняется единице.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Например, \(\frac67\) — это 6 частей из 7.
В такой форме можно записать любое рациональное число, в том числе целое. При этом в качестве знаменателя может выступать любое натуральное число.
Так, единицу можно представить как \(\frac88,\;\frac<13><13>,\;\frac<857><857>\) и так далее.
Для записи чисел больше одного в дробной форме необходимо это число умножить на числитель:
Существует понятие правильных и неправильных дробей.
Правильной называют дробь, у которой модуль числителя меньше модуля знаменателя.
Соответственно, у неправильной дроби числитель больше или равен знаменателю. Из приведенных выше примеров \( \frac67\) — правильная дробь, а \(\frac88,\;\frac<13><13>,\;\frac<857><857>\) и \(\frac<10>5\) — неправильные.
Формы дробной записи
Как уже описывалось выше, стандартный способ записи обыкновенных дробей — через горизонтальную черту. Числитель помещается сверху, знаменатель — под чертой: \(\frac mn.\)
Один из самых распространенных и часто используемых на практике методов записи дробей — десятичная дробь. В этом случае число записывается как результат деления числителя на знаменатель. При этом, целая часть отделяется от остаточной при помощи запятой (в стандарте стран СНГ) или точкой.
По своей сути, все десятичные дроби являются смешанными числами.
Понятие смешанного числа
Смешанное число — комбинация целочисленной и дробной форм записи рациональных чисел.
Как соотносятся между собой неправильные дроби и смешанные числа
Неправильные дроби отличаются от правильных тем, что в них числитель больше знаменателя. То есть, если представлять их буквально как операцию деления, то делимое больше делителя. Это значит, что в них содержится целая часть, выделив которую можно получить смешанное число.
Необходимость и алгоритм преобразования
При решении задач зачастую необходимо преобразовать смешанные числа в дробные, так как с ними проще проводить вычисления.
Как перевести смешанное число в неправильную дробь
Чтобы записать смешанное число в форме неправильной дроби необходимо выполнить два действия: умножить целую часть на знаменатель и прибавить полученный результат к числителю.
Этот упрощенный способ преобразования работает на том принципе, что любое целое число можно представить в виде произведения этого числа на единицу. Единицу же в свою очередь можно представить в виде дроби, где числитель равен знаменателю. Разберем предыдущий пример более подробно:
Как выделить из неправильной дроби целую часть
Обратное преобразование работает на принципе, согласно которому, при делении двух некратных друг другу чисел, делимое можно представить в виде суммы кратного делителю числа и некоего остатка. В качестве примера возьмем число из предыдущего пункта:
В этом преобразовании можно пойти дальше и представить смешанное число в виде десятичной дроби. Для этого целая часть отделяется запятой, а операция деления продолжается с остатком, умноженным на 10. Само деление продолжается до тех пор, пока остаток не окажется равен нулю.
В случае с бесконечными десятичными дробями, деление продолжается до тех пор, пока число знаков после запятой не удовлетворит условие задачи. В таком случае, последняя цифра округляется согласно установленным правилам.
Неправильная дробь
Что такое неправильная дробь
Неправильной называется дробь, числитель которой по своей величине превышает знаменатель либо одинаков с ним.
Основные математические действия с неправильными дробями
Неправильная дробь — полноценный представитель числового множества, поэтому с ней можно производить основные математические действия:
Сравнение
6 / 5 7 / 5 ; 9 / 7 > 8 / 7 ; 5 / 5 = 5 / 5
Однако, бывает необходимо вычислить, насколько значение неправильной дроби больше (либо меньше) значения другой неправильной дроби с иным знаменателем.
Сложение
Определить сумму двух неправильных дробей с одинаковым знаменателем легко: 5/4+7/4=12/4=3
Схематически это можно записать с помощью формулы:
Сложение неправильных дробей с различными знаменателями. Для таких случаев существует два варианта: перевести дроби в смешанные либо использовать правило для перехода к общему знаменателю.
Переход к смешанным дробям осуществляется путем деления числителя на знаменатель (бывает, что с остатком):
Тактика приведения к общему знаменателю при сложении неправильных дробей (и их вычитании) следующая:
Аналогичным образом поступают, когда необходимо провести вычитание с неправильными дробями.
Умножение
При умножении друг на друга двух неправильных дробей получается дробь, числитель которой равен произведению числителей первоначальных дробей, а знаменатель — произведению знаменателей.
Деление
При делении неправильных дробей деление имеет обратное свойство. Делитель необходимо записать наоборот: числитель и знаменатель поменять местами. Когда это проведено, делимое умножают на делитель и получают искомый результат.
Перевод неправильной дроби в смешанную дробь и обратно
Неправильную дробь можно легко перевести в смешанную, произведя следующие действия:
Например, необходимо превратить в смешанную дробь 13/8.
Разделив 13 на 8, получаем 1 и 5/8. Разделив 5 на 8, получаем 0,625. В итоге 1,625.
Бывают случаи, когда нужно произвести обратное действие: превратить смешанную дробь в неправильную. Объяснение изложено в следующей формуле:
Подставим в эту формулу значения. 21 / 3 = ( 1 + 2 * 3 ) / 3 = 7 / 3
Примеры задач
Рассмотрим приведенные выше правила на примерах.
Сложение с одинаковым знаменателем: 8 / 5 + 7 / 5 = 15 / 5 = 3
Объяснение: приводим слагаемые к общему знаменателю. Для этого на знаменатель правой дроби умножаем числитель левой, а знаменатель левой — на числитель правой. В знаменателе дроби-произведения стоит произведение обоих знаменателей. После проведения расчетов получается смешанная дробь 3,625.
Объяснение: приводим вычитаемые к общему знаменателю. Для этого на знаменатель правой дроби умножаем числитель левой, а знаменатель левой — на числитель правой. В знаменателе дроби-частного стоит произведение обоих знаменателей. После проведения расчетов получается смешанная дробь 3,875.
Задача на умножение:
7 / 5 * 9 / 4 = 63 / 20
8 / 6 * 10 / 9 = 80 / 54
Объяснение: умножаем числитель на знаменатель и получаем искомое произведение.
4 / 7 : 2 / 5 = 4 / 7 * 5 / 2 = ( 4 * 5 ) / ( 7 * 2 ) = 20 / 14 = 16 / 14
Поменяв местами числитель и знаменатель в делителе, производим действие умножения двух дробей. После этого в числителе итоговой дроби ставится произведение двух числителей, а в ее знаменателе — произведение двух знаменателей.
Смешанные числа, перевод смешанного числа в неправильную дробь и обратно
В этом материале мы разберем такое понятие, как смешанные числа. Начнем, как всегда, с определения и небольших примеров, потом поясним связь смешанных чисел и неправильных дробей. После этого мы изучим, как правильно выделять целую часть из дроби и получать в результате целое число.
Понятие смешанного числа
Числа вида 0 3 14 также не относятся к смешанным. Здесь не выполняется первая часть условия: целая часть должна быть представлена только натуральным числом, а нуль им не является.
Как соотносятся между собой неправильные дроби и смешанные числа
Эту связь проще всего проследить на конкретном примере.
Наш пример доказывает, что в виде смешанного числа можно представить любую неправильную дробь.
Мы поняли, как приводить неправильную дробь к виду смешанного числа. Если в числителе неправильной дроби стоит такое число, которое можно разделить на знаменатель без остатка, то можно сделать это, и тогда наша неправильная дробь станет натуральным числом.
Как перевести смешанное число в неправильную дробь
Чтобы успешно решать задачи, полезно уметь производить и обратное действие, то есть делать из смешанных чисел неправильные дроби. В этом пункте мы разберем, как правильно это сделать.
Для этого нужно воспроизвести следующую последовательность действий:
1. Для начала представляем имеющееся смешанное число n a b как сумму целой и дробной части. Получается n + a b
2. Далее заменяем целую часть на дробь со знаменателем, равным единице (то есть записываем n как n 1 ).
Разберем это действие на конкретном примере.
Представьте 5 3 7 в виде неправильной дроби.
Решение
Последний шаг – сложение дробей, имеющих разные знаменатели:
5 1 + 3 7 = 35 7 + 3 7 = 38 7
Представьте 15 2 5 в виде неправильной дроби.
Решение
Как выделить из неправильной дроби целую часть
Обычно мы не указываем неправильную дробь в качестве итогового ответа. Принято доводить вычисления до конца и заменять ее либо натуральным числом (разделив числитель на знаменатель), либо смешанным числом. Как правило, первый способ используется, когда разделить числитель на знаменатель можно без остатка, а второй – если такое действие невозможно.
Когда мы выделяем из неправильной дроби целую часть, мы просто заменяем ее равным смешанным числом.
Разберем, как именно это делается.
Приведем доказательство этого утверждения.
Выделение целой части из неправильной дроби a b осуществляется таким образом:
1) производим деление a на b с остатком и записываем неполное частное q и остаток r отдельно.
Представьте 107 4 в виде смешанного числа.
Решение
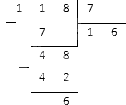
Делим 104 на 7 столбиком:
Нам осталось посмотреть, как заменить неправильную дробь натуральным числом (при условии, что ее числитель делится на знаменатель без остатка).
Как перевести смешанную дробь в неправильную и наоборот
Объяснения с примерами
Как перевести смешанную дробь в неправильную
Смешанная дробь — это запись целого числа с обыкновенной дробью.
Читается 5 целых три восьмых.
Чтобы нагляднее себе представить, можно мысленно добавлять знак «+» между целым числом и обыкновенной дробью. И это не будет ошибкой, так как знак «плюс» для упрощения записи опускается.
Эта запись означает 5 целых пирогов и 3 восьмых пирога.
5 площадей определенных размеров и 3 восьмых данной площади.
Неправильная дробь — эта та, у которой числитель больше знаменателя. Соответственно, из неё можно выделить 1 целое число или больше. Так как любая неправильная дробь больше единицы.
Можно сделать действие и наоборот — превратить смешанное число в неправильную дробь.
Чтобы перевести смешанное число в неправильную дробь нужно целое число умножить на знаменатель и прибавить числитель. Полученное значение записываем в числитель. Знаменатель оставляем без изменений.
Объяснение почему именно так мы переводим:
Целое число мы можем записать дробью, как сорок восьмых (40: 8 = 5). Не забывайте, что дробь — это деление. Число 40 мы получаем умножением целого числа на знаменатель. Теперь нам осталось сложить две дроби с одинаковыми знаменателями.
Примеры для перевода смешанных дробей в неправильные
Как перевести неправильную дробь в смешанную
Как мы уже говорили, неправильная дробь всегда больше единицы.
Чтобы перевести неправильную дробь в смешанную нужно начать делить числитель на знаменатель до целых. Полученное целое число пишем перед дробью, остаток деления — в числитель. Знаменатель остаётся без изменения.
Схема для запоминания:
Примеры
Как перевести неправильную дробь в правильную
Смешанную дробь иногда называют правильной, поэтому объяснение перевода будет являться дублированием предыдущего абзаца. Если у вас остались вопросы, то смотрите разбор в видео:
Как перевести в неправильную дробь

Всего получено оценок: 172.
Всего получено оценок: 172.
Перевод неправильной дроби – это необходимая процедура для правильной записи ответа. К тому же в некоторых ситуациях, куда удобнее вести вычисления со смешанными дробями, нежели с неправильными числами. Рассмотрим правила перевода неправильных дробей в смешанные числа.
Виды дробей
Дроби можно разделить на:
Помимо этого все дроби, как и другие числа, делятся на положительные и отрицательные.
Если числитель больше знаменателя, то дробь неправильная. Если числитель меньше знаменателя – правильная. Но нет названия для дроби, у которой числитель и знаменатель равны, так как она автоматически превращается в единицу. Как только в расчетах ученик видит такую ситуацию, следует сразу же преобразовать число в 1.
Перевод неправильной дроби в смешанное число
Для того, чтобы перевести неправильную дробь в смешанное число, нужно выделить в ней целую часть. Для этого числитель делится на знаменатель с остатком. Результат такого деления это целая часть числа, а остаток это числитель дробной части. При этом знаменатель нового числа будет таким же, как и знаменатель дроби.
Значит, перевод будет выглядеть так:
Можно как перевести в неправильную дробь смешанное число, так и наоборот: выделить целую часть в неправильной дроби. Ученик выполняет эти действия для записи ответа или облегчения расчетов. Но нельзя превратить неправильную дробь в правильную и наоборот. Это два разных вида чисел, которые между собой никак не связаны.
Что мы узнали?
Мы поговорили о правиле перевода неправильной дроби в смешанное число. Сказали, как правильно выделить целую часть дроби, и привели пример. Также отметили, что нельзя превратить неправильное число в правильное.