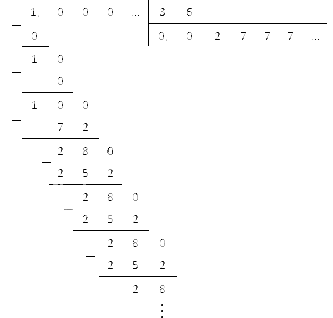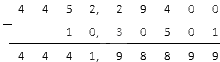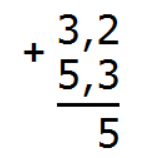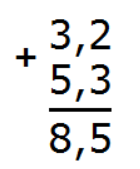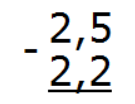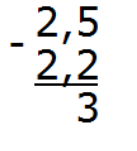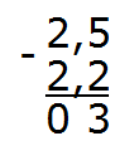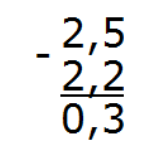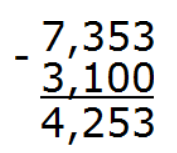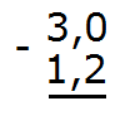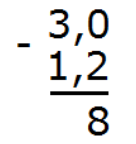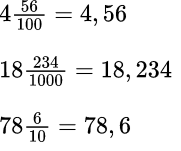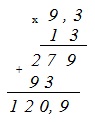Как отнимать десятичные дроби в столбик
Вычитание десятичных дробей
Также как и сложение, вычитание десятичных дробей производим по правилам вычитания в столбик натуральных чисел.
Основные правила вычитания десятичных дробей.
Как вычитать десятичные дроби другим способом
Если вы чувствуете себя уверенно в десятичных дробях и хорошо понимаете, что называется десятыми, сотыми и т.д., предлагаем вам попробовать другой способ вычитания (сложения) десятичных дробей без их записи в столбик.
Другой способ вычитания десятичных дробей, как и сложение, основывается на трёх основных правилах.
Вычитают десятичные дроби справа налево. То есть, начиная с самой правой цифры после запятой.
Вычитать нужно по цифрам разрядов. Целые из целых, десятые из десятых, сотые из сотых, тысячные из тысячных и т.д.
При вычитании большей цифры из меньшей, у соседа слева меньшей цифры занимаем десяток.
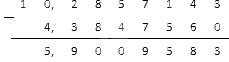
Как обычно, рассмотрим пример:
Вычитаем справа налево с самой правой цифры. У нас самая правая цифра в обеих дробях — сотые. 1 — в первом числе, 1 — во втором. Вот их и вычитаем.
И наконец, вычитаем целые части. 14 — в первом числе (не забудьте, что мы из 5 вычли 1 ), 8 — во втором числе.
Десятые можно вычитать только из десятых, сотые из сотых, тысячные из тысячных и т.д. Если в одной из десятичных дробей, отсутствует цифра нужного разряда, вместо неё пишем ноль.
Во втором числе самая правая цифра это 2 (сотые), а в первом числе сотых нет в явном виде. Поэтому, к первому числу справа от 9 добавляем ноль и вычитаем согласно основным правилам.
вычесть из целого десятичную
Как вычесть из целого десятичную, сколько возможных вариантов существует!? Можно вычитать из целого десятичную дробь столбиком, либо на калькуляторе. И конечно же наоборот : вычитание из десятичной целое число.
И еще вариант, когда второе число(вычитаемое) будет больше чем первое число(уменьшаемое.)
О вычитании целого из десятичной дроби и наоборот!
Правило вычитания десятичной из целого
Такого правила не существует, потому, что это частный случай такого действия, как вычитание столбиком
Давайте попробуем разобраться на примере:
Пример : Как вычесть десятичную из целого
Располагаем 5, над целым числом десятичной дроби, если это ноль, то располагаем над ним.
Результат вычитания из целого числа десятичной дроби :
Как вычесть целое из десятичной дроби?
Для вычитания целого из десятичной дроби нам опять понадобится какой-то пример, пусть это будет :
С этим примером, вообще, очень просто! Ставим целое число под целым числом целое число.
Десятичные сносим, под черту без изменений.
Результат вычитания целого из десятичной дроби :
Как вычесть из десятичной целое на калькуляторе!?
Для калькулятора нет никакой разницы или это:
вычитание из десятичной дроби целого числа либо :
вычитание целого числа из десятичной дроби
Рассмотрим простой пример, что разбирали выше :
Получаем результат вычитания из целого десятичной дроби :
Как вычитать из десятичной целое, если десятичная меньше целого
Или же возьмем обратный вариант :
Как вычитать целое число из десятичной дроби, если целое меньше десятичной дроби!?
В качестве пример, возьмем выше приведенный пример, но только поменяем местами уменьшаемое и вычитаемое.
Меняем местами и в результат добавляем минус.
Вычитание десятичных дробей: правила, примеры, решения
Изучаем другие действия, которые можно совершать с десятичными дробями. В этом материале мы узнаем, как правильно подсчитать разность десятичных дробей. Отдельно разберем правила для конечных и бесконечных дробей (как периодических, так и непериодических), а также посмотрим, как считать разность дробей столбиком. Во второй части мы объясним, как вычесть десятичную дробь из натурального числа, обыкновенной дроби, смешанного числа.
Отметим заранее, что в этой статье рассмотрены только случаи, когда меньшая дробь вычитается из большей, т.е. результат этого действия положителен; другие случаи относятся к нахождению разности рациональных и действительных чисел и должны быть объяснены отдельно.
Основные правила вычитания десятичных дробей
Процесс вычисления как конечных, так и бесконечных периодических десятичных дробей можно свести к нахождению разности дробей обыкновенных. Раньше мы говорили о том, что десятичные дроби можно записывать в виде обыкновенных дробей. Исходя из этого правила, разберем несколько примеров нахождения разности.
Решение
Подсчеты, связанные с десятичными дробями, удобно производить столбиком. Как же пользоваться этим методом? Покажем, решив задачу.
Решение
Переведем записи периодических дробей в обыкновенные и подсчитаем.
Если нужно, ответ мы можем представить в виде десятичной дроби:
Разберем далее, как найти разность, если у нас в условиях стоят бесконечные непериодические дроби. Такой случай также можно свести к нахождению разности конечных десятичных дробей, для чего понадобится округлить бесконечные дроби до определенного разряда (обычно самого меньшего из возможных).
Решение
Как считать разность десятичных дробей столбиком
Вычитание столбиком – быстрый и наглядный способ узнать разность конечных десятичных дробей. Процесс подсчета очень схож с аналогичным для натуральных чисел.
Чтобы подсчитать разность десятичных дробей столбиком, необходимо:
Разберем конкретный пример использования этого метода на практике.
Решение
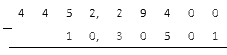
Запишем получившиеся числа друг под другом в нужном порядке, чтобы получился столбик:
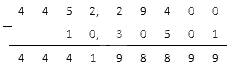
Считаем как обычно, игнорируя запятые:
В получившемся ответе поставим запятую в нужном месте:
Как вычесть натуральное число из десятичной дроби и наоборот
Найти разность между конечной десятичной дробью и натуральным числом легче всего описанным выше способом – столбиком. Для этого число, из которого мы вычитаем, необходимо записать в виде десятичной дроби, в дробной части которой стоят нули.
Если из натурального числа нам нужно вычесть бесконечную периодическую дробь, то мы опять же сводим эту задачу к аналогичному вычислению. Заменяем периодическую десятичную дробь на обыкновенную.
Решение
Если данная в условии дробь непериодическая, поступаем так же, предварительно округлив ее до нужного разряда.
Решение
Если перед нами стоит обратная задача – вычесть натуральное число из десятичной дроби, то мы выполняем вычитание из целой части дроби, а дробную часть не трогаем совсем. Мы поступаем так и с конечными, и с бесконечными дробями.
Решение
Как вычесть десятичную дробь из смешанного числа или обыкновенной дроби и наоборот
Эту задачу также необходимо свести к вычитанию обыкновенных дробей – как в случае со смешанными числами, так и с десятичными дробями.
Решение
Если в условии стоит смешанное число, из которого надо вычесть конечную или периодическую десятичную дробь, то поступаем аналогично.
Таким же образом мы действуем, когда вычитаем смешанное число или обыкновенную дробь из конечной или периодической дроби.
Решение
Если нам требуется выполнять вычитание с участием бесконечных непериодических дробей, то нам нужно будет свести их к конечным. Со смешанными числами поступаем аналогично. Для этого запишем обыкновенную дробь или смешанное число в виде десятичной дроби и округлим вычитаемую дробь до определенного разряда. Проиллюстрируем нашу мысль примером:
Решение
Преобразуем смешанное число в неправильную дробь.
10 2 7 = 10 · 7 + 2 7 = 72 7
Единственное, что осталось сделать – вычесть одну конечную десятичную дробь из другой. Выполним подсчет столбиком:
Сложение и вычитание десятичных дробей
Понятие десятичной дроби
Прежде, чем перейдем к тому, как выполнить сложение и вычитание десятичных дробей, разберемся в основных определениях, видах дробей и разницей между ними.
Дробь — это число в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которое можно представить число. Есть два формата записи:
В обыкновенной дроби над чертой принято писать делимое, которое становится числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление.
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. По сути, десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Ее записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
Конечная десятичная дробь — это когда количество цифр после запятой точно определено.
Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.
Свойства десятичных дробей
Главное свойство десятичной дроби звучит так: если к десятичной дроби справа приписать один или несколько нулей — ее величина не изменится. Это значит, что если в вашей дроби куча нулей — их можно просто отбросить. Например:
Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:
Курсы ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.
Сложение десятичных дробей
Мы знаем, что десятичная дробь состоит из целой и дробной части. При сложении десятичных дробей нужно отдельно сложить каждую часть.
Рассмотрим пример сложения 3,2 и 5,3. Для удобства используем метод столбика.
Запишем эти две дроби в столбик. При этом целая часть одной дроби должна быть под целой частью другой. В школе это называют «запятая под запятой». Вот так:
Складываем дробные части: 2 + 3 = 5. Запишем пятерку в дробной части ответа:
Теперь целые части: 3 + 5 = 8. Запишем восьмерку в целой части ответа:
Отделим запятой целую часть от дробной, чтобы запятая была под запятой:
Получили ответ: 3,2 + 5,3 = 8,5.
Вычитание десятичных дробей
Процесс вычитания десятичных дробей очень похож на сложение. Будем использовать те же правила: «запятая под запятой» и «равное количество цифр после запятой».
Пример 1. Найти значение выражения 2,5 − 2,2
Запишем в столбик выражение так, чтобы запятая была под запятой:
Вычислим дробную часть 5 − 2 = 3. Запишем тройку в десятой части ответа:
Вычислим целую часть 2 − 2 = 0. Запишем ноль в целой части ответа:
Отделим запятой целую часть от дробной:
Вот и ответ: 2,5 − 2,2 = 0,3.
Пример 2. Вычислить: 7,353 – 3,1
В этом выражении разное количество цифр после запятой: в 7,353 три цифры после запятой, а в 3,1 только одна. Значит в дроби 3,1 в конце добавим два нуля, чтобы уравнять количество цифр в обеих дробях. То есть: 3,1 = 3,100.
Запишем в столбик и посчитаем:
Ответ: 7,353 – 3,1 = 4,253.
Пример 3. Вычислить: 3 − 1,2
В этом примере из целого числа нужно вычесть десятичную дробь. Запишем это выражение столбиком так, чтобы целая часть десятичной дроби 1,23 была под числом 3. Вот так:
Сделаем количество цифр после запятой одинаковым:
Теперь вычитаем десятые части: 0 − 2. От нуля невозможно вычесть число 2. Поэтому займем единицу у соседнего разряда. Таким образом 0 превращается в число 10. Вычисляем десятые части: 10 − 2 = 8. Запишем восьмерку в десятой части ответа:
Сейчас вычтем целые части. В самом начале было число 3, но мы заняли у него единицу, поэтому оно обратилось в двойку. Поэтому: 2 − 1 = 1. Запишем единицу в целой части ответа:
Отделим запятой целую часть от дробной:
Мы рассмотрели несколько примеров сложения и вычитания десятичных дробей. Чтобы каждый ученик в 5 и 6 классе мог повторить эту последовательность, есть специальный алгоритм:
Алгоритм сложения (вычитания) десятичных дробей
Проще говоря, правило сложения (вычитания) десятичных дробей звучит так: чтобы сложить (вычесть) две десятичные дроби, нужно записать их в столбик друг под другом, запятая под запятой. А потом сложить (вычесть) как обыкновенные числа и снести запятую.
Десятичные дроби
теория по математике 📈 числа и вычисления
Десятичная дробь — дробь, которая представляет собой способ представление числа в виде записи числа с запятой, где цифры перед запятой называются целой частью, а цифры после запятой – дробной частью (десятичной частью).
Десятичные дроби получают из записи обыкновенных дробей со знаменателем 10, 100, 1000 и так далее. Например, десятичные дроби:
4,56 – четыре целых пятьдесят шесть сотых 18,234 – восемнадцать целых двести тридцать четыре тысячных 78,6 – семьдесят восемь целых шесть десятых
Чтение десятичных дробей
Чтение десятичной части (десятых, сотых и так далее) зависит от количества цифр после запятой. Если цифра одна, то читают – десятых (в числе десять — один нуль, это соответствует одной цифре). Если две цифры после запятой, то читают – сотых (в сотне два нуля).
Десятичные дроби получаются из обыкновенных дробей:
Сложение (вычитание) десятичных дробей
Чтобы сложить (вычесть) в столбик две десятичные дроби нужно:
Если складывают (вычитают) целое число и десятичную дробь, то нужно поставить запятую после целого числа и приписать необходимое количество нулей после запятой.
Пример №1. Запись, где запятая под запятой и соответствующий разряд под соответствующим.
34,145 + 5,678 = 39,823
Пример №2. Запись, где также запятая под запятой, а во втором числе дописан нуль, чтобы уравнять количество знаков после запятой.
Пример №3. В первом слагаемом нет десятичной части, поэтому, после числа 56 поставили запятую и добавили нужное количество нулей.
Умножение десятичных дробей
При умножении двух десятичных дробей в столбик необходимо:
Пример №4. Запись выполнена так, что цифры по правому краю записаны ровно одна под одной, то есть как при обычном умножении чисел в столбик. Умножение выполнено без учета запятой. В ответе справа отделены 4 цифры запятой, так как в первом множителе их 3 после запятой, а во втором – одна, в двух множителях вместе – четыре.
0,125 × 2,3 00375 0250 0,2875
Пример №5. Здесь показано умножение десятичной дроби и целого числа. Умножение выполнено без учета запятой. В ответе отделена справа запятой только одна цифра, так как только в первом множителе есть десятичная часть с одной цифрой после запятой.
Умножение десятичных дробей на 10, 100, 1000…
Чтобы умножить десятичную дробь на 10, 100, 1000 и так далее, нужно перенести запятую вправо на столько цифр, сколько нулей у множителя. Умножение в данном случае выполняется в строчку.
Пример №6. 2,456 × 10 = 24,56 Запятую в десятичной дроби перенесли вправо на 1 цифру, так как у 10 один нуль.
Пример №7. 0,45678 × 100 = 45,678 Запятую перенесли вправо на 2 цифры, так как у 100 два нуля. Нуль, стоящий в начале десятичной дроби, убрали, так как впереди целой части, отличной от нуля он не пишется.
Пример №8. 9,46 × 1000 = 9460 в данном случае при переносе запятой на три цифра не хватило одной, поэтому в конце числа приписали нуль, и в ответе получилось целое число.
Умножение десятичной дроби на разрядную единицу 0,1; 0,01; 0,001…
При умножении десятичной дроби на разрядную единицу 0,1; 0,01; 0,001 (и так далее) нужно перенести запятую на столько цифр влево, сколько цифр в данной разрядной единице после запятой. Умножение обычно выполняется в строчку устно.
Пример №9. 983,7821 × 0,01= 9,837821 Переносим запятые влево на 2 цифры, так как в числе 0,01 две цифры после запятой.
Пример №10. 8,7654 × 0,1 = 0,87654 Перенесли на 1 цифру влево, так как в числе 0,1 одна цифра после запятой. В данном случае перед 8 появился нуль, так как при переносе запятой слева цифр не оказалось.
Пример №11. 7,98 × 0,0001 = 0,000798 При переносе влево на 4 цифры не хватило трех, поэтому впереди поставили нули, а также нуль образуется и в целой части.
Деление десятичных дробей
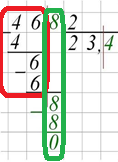
Пример №12. Деление десятичной дроби на целое число. 46,8 : 2 = 23,4
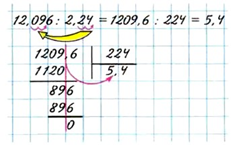
Пример №13. Деление десятичной дроби на десятичную дробь. 12,096 : 2,24 = 5,4 Из данного примера видно, что деление десятичных дробей обязательно сводится к делению на целое число.
Пример №14. 276,3 : 0,003 = 276300 : 3 = 92100. Здесь видно, что не хватает двух цифр в числе 276,3 и поэтому при переносе запятой к нему приписали два нуля. Затем выполнили деление двух целых чисел.
Деление десятичной дроби на 10, 100, 1000…
При делении десятичной дроби на 10,100, 1000 и так далее нужно перенести запятую на столько цифр влево, сколько нулей в данном числе. Деление выполняется в строчку устно.
Пример №16. 134,987 : 1000 = 0,134987 Перенесли запятую на три цифры влево, так как у 1000 три нуля. В целой части поставили нуль, так как цифр не хватило.
Пример №17. 7,234 : 100 = 0,07234 Перенесли запятую влево на две цифры. Так как цифр не хватало, то недостающие заменили нулями.
Деление десятичной дроби на разрядную единицу 0,1; 0,01; 0,001…
При делении десятичной дроби на разрядную единицу 0,1; 0,01; 0,001 и так далее нужно перенести запятую на столько цифр вправо, сколько цифр в данной разрядной единице после запятой. Деление обычно выполняется в строчку устно.
Пример №19. 41,234 : 0,01 = 4123,4 Перенос запятой на 2 цифры вправо, так как в числе 0,01 две цифры после запятой.
Пример №20. 56,91 : 0,001 = 56910 При переносе запятой на три цифры вправо приписали один нуль, так как одной цифры не хватило.
Сформируем из чисел ряд от наименьшего из них до наибольшего. Для этого сначала разделим их на положительные и отрицательные. И сразу получим наибольшее в ряду (поскольку оно единственное больше нуля): 0,021.
Три оставшихся отрицательных распределим по их модулям. Известно, что из двух отрицательных чисел больше то, у которого модуль меньше. Тогда получаем, что –0,304
pазбирался: Даниил Романович | обсудить разбор | оценить
Для получения результата необходимо последовательно выполнить математические действия в соответствии с их приоритетом.
Выполняем возведение в степень. Получаем числа, состоящие из единицы и следующего за ней количества нулей, равного показателю степени. При этом знаки «–» в скобках исчезают, поскольку показатели степеней четные. Получаем:
Выполняем умножение. Для этого в числе 0,3 переносим десятичную запятую на 4 знака вправо (так как в 10000 четыре нуля), а к 4 дописываем, соответственно, 2 нуля. Получаем:
Выполняем сложение –3000+400. Поскольку это числа с разными знаками, то вычитаем из большего модуля меньший и перед результатом ставим «–», поскольку число с большим модулем отрицательное. Получаем:
Так как оба числа отрицательные, то складываем их модули и перед результатом ставим «–». Получаем:
pазбирался: Даниил Романович | обсудить разбор | оценить
Это задание требует простого умения выполнять арифметические действия с десятичными дробями.
Сначала выполняем умножение. Умножаем –13 и –9,3 в столбик без учета знаков «–» перед сомножителями. В полученном произведении отделяем одну – последнюю – цифру десятичной запятой:
Знак произведения будет положительным, поскольку умножаются два отрицательных числа. Получаем:
Эту разность можно вычислить в столбик, но можно и устно. Выполним это действие в уме: вычитаем отдельно целые части и десятичные. Получаем:
pазбирался: Даниил Романович | обсудить разбор | оценить
Задачу можно решать разными путями, а именно менять последовательность действий, но этот вариант решения рекомендуется для тех, кто уверен в своих возможностях и знает математику на отлично. Для остальных мы рекомендуем выполнить последовательно действия в числителе и знаменателе, а затем разделить числитель на знаменатель. Числитель вычислять в данном примере нет необходимости, это число 9.
Вычислим значение знаменателя:
Можно произвести вычисления в столбик, тогда получим:
Либо перевести дробь к простому виду:
4,5 • 2,5 = 4½ • 2 ½ = 9 / 2 • 5 / 2 = 45 / 4
Последний случай предпочтительней, так как для дальнейшей операции — деления числителя на знаменатель задача упрощается. Делим числитель на знаменатель, умножая числитель на перевернутую дробь в знаменателе:
9 / ( 45 / 4 ) = ( 9 / 1 ) • ( 4 / 45 ) = ( 9 • 4 ) / (1 • 45 )
9 и 45 можно сократить на 9:
( 9 • 4 ) / (1 • 45 ) = ( 1 • 4 )/ (1 • 5 ) = 4 / 5 = 8 / 10 = 0,8
pазбирался: Даниил Романович | обсудить разбор | оценить