Как определить скорость автомобиля в задаче
Как определить скорость автомобиля в задаче
1 мин = 60 с; 1 ч = 3600 с; 1 км = 1000 м; 1 м/с = 3,6 км/ч.
Физика 7 класс: все формулы и определения КРУПНО на трех страницах
ПРИМЕРЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ
Задача № 1. Ласточка летит со скоростью 36 км/ч. Какой путь она преодолеет за 0,5 ч?
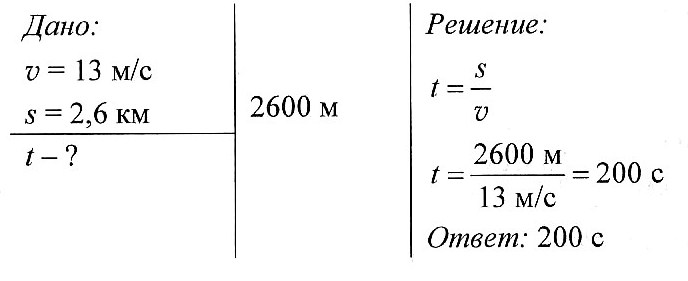
Задача № 1. Конькобежец может развивать скорость до 13 м/с. За какое время он пробежит дистанцию длиной 2,6 км?
Задача № 3. Автомобиль «Чайка» развивает скорость до 160 км/ч, а почтовый голубь — до 16 м/с. Сможет ли голубь обогнать автомобиль?
Решение. Чтобы сравнить скорости движения тел, надо перевести их в одинаковые единицы измерения. Перевод скорости из одних единиц в другие выполняют следующим образом. 160 км = 160000 м, 1 ч = 3600 с. Следовательно, за 1 с автомобиль пройдет путь 160000 : 3600 = 44 (м), значит: 
Ответ: Голубь не обгонит автомобиль, так как 16 м/с
Задача № 4. Вдоль дороги навстречу друг другу летят скворец и комнатная муха. На рисунке представлены графики движения скворца (I) и мухи (II). Пользуясь графиком, определите:
1) Каковы скорости движения скворца и мухи?
2) Через сколько секунд после начала движения они встретятся?
3) Какое расстояние они пролетят до места встречи?
Решение.
1. Скорость движения скворца определим по формуле v=S/t. Выберем на графике произвольное время и определим, какое расстояние за это время пролетел скворец. Видно, что за 5 с скворец пролетел 100 м. Тогда 
Аналогично найдем скорость движения мухи:

2. Точка А (точка пересечения графиков движения) соответствует моменту встречи. Скворец и муха встретятся через 4 секунды.
3. Скворец до места встречи пролетит расстояние SI = 80 м. Муха пролетит расстояние SII = 100 м — 80 м = 20 м.
Ответ: 1) скворец 20 м/с, муха 5 м/с, 2) через 4 с, 3) скворец 80 м, муха 20 м
Задача № 5. Определите среднюю скорость движения плота, если за 20 минут он переместился на 900 м. Скорость выразить в км/ч.
Ответ: Средняя скорость плота 2,7 км/ч.
Задача № 6. Стоящий на эскалаторе человек поднимается за 2 мин, а бегущий по эскалатору — за 40 с. За какое время этот человек поднимется по неподвижному эскалатору?
ОТВЕТ: 1 мин.
Задача № 7. Моторная лодка за 3 ч проходит расстояние от города до поселка, расположенного ниже по течению реки. Сколько времени займет обратный путь, если скорость движения лодки относительно воды в 4 раза больше скорости течения?
ОТВЕТ: 5 ч.
Задача № 8 (повышенной сложности). Рыбак плыл по реке на лодке, зацепил шляпой за мост, и она свалилась в воду. Через час рыбак спохватился, повернул обратно и подобрал шляпу на 4 км ниже моста. Какова скорость течения? Скорость лодки относительно воды оставалась неизменной по модулю.
ОТВЕТ: 2 км/ч.
Задача № 9 (олимпиадного уровня). Из городов А и Б навстречу друг другу по прямому шоссе одновременно выехали два велосипедиста. Скорость первого 10 км/ч, скорость второго 15 км/ч. Одновременно с велосипедистами из города А вылетела ласточка. Она долетает до второго велосипедиста, разворачивается, Долетает до первого велосипедиста и летает так между ними до тех пор, пока велосипедисты не встретятся. Какой путь пролетела ласточка, если скорость ее движения 50 км/ч, а расстояние между городами 100 км? Временем разворота ласточки можно пренебречь.
ОТВЕТ: 200 км.
Алгоритм решения задач на движение
При решении других задач прямолинейного равномерного движения в общем виде нужно придерживаться следующего алгоритма: 1) выбрать систему отсчёта; 2-3) определить начальные координаты и значения скоростей движения тел в этой системе отсчёта; 4) записать зависимости координат тел от времени; 5) записать в виде уравнения условие задачи; 6) объединить уравнения; 7) решить эти уравнения; 8) провести анализ полученного результата (после чего выяснить, имеет ли полученный результат физический смысл); 9) если в условии задачи даны числовые значения, необходимо подставить их в полученное выражение и получить числовой ответ.
Анализ полученного результата заключается в исследовании зависимости искомой величины от входящих в ответ величин.
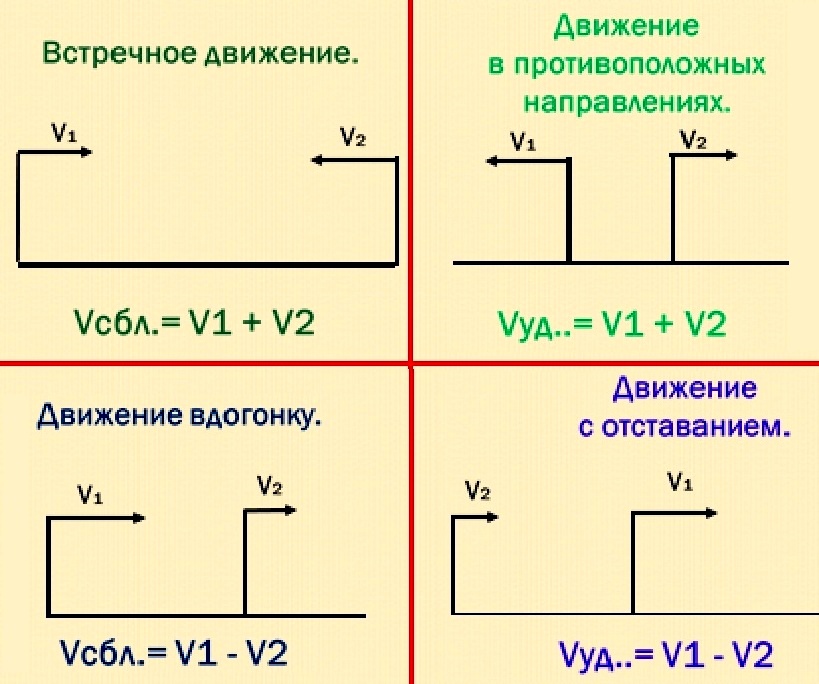
Не стоит забывать и про направление движения в зависимости от типа задачи (встреча, погоня, обгон, отставание)
Конспект урока «Задачи на движение с решением».
Задачи на скорость, время и расстояние
Скорость — это расстояние, пройденное за единицу времени: за 1 секунду, за 1 минуту, за 1 час и так далее.
Разные объекты имеют разную скорость. Например, средняя скорость пешехода составляет 5 километров в час, скорость велосипедиста — 12 км в час, а автомобиля — 80 км в час. При записи скорости, предлог в заменяют наклонной чертой — км/ч (например, 15 км/ч).
Если весь путь проходится с одинаковой скоростью, то такое движение называется равномерным. Далее будут рассмотрены задачи только на равномерное движение.
Нахождение скорости
Чтобы найти скорость по данному пути (расстоянию) и времени, надо путь разделить на время.
скорость = расстояние : время
Задача 1. Поезд проехал 320 км за 4 часа. Чему равна скорость поезда?
Решение: Чтобы найти скорость поезда, надо расстояние, которое прошёл поезд (320 км), разделить на время поезда в пути (4 ч):
Ответ: Скорость поезда равна 80 км/ч.
Задача 2. Турист за 3 часа прошёл 12 км, а велосипедист за 2 часа проехал 24 км. Во сколько раз турист движется медленнее велосипедиста?
Решение: Чтобы узнать во сколько раз скорость туриста меньше, чем у велосипедиста, надо узнать их скорость, разделив пройденные расстояния на затраченное время:
12 : 3 = 4 (км/ч) — скорость туриста,
24 : 2 = 12 (км/ч) — скорость велосипедиста.
Теперь осталось узнать на сколько медленнее движется турист, для этого надо большее число разделить на меньшее:
Ответ: Турист движется в 3 раза медленнее, чем велосипедист.
Нахождение времени
Чтобы найти время по данному расстоянию и скорости, надо расстояние разделить на скорость.
время = расстояние : скорость
Задача. Лодка преодолела путь в 100 км со скоростью 20 км/ч. Сколько времени плыла лодка?
Ответ: Лодка плыла 5 часов.
Нахождение расстояния
Чтобы найти расстояние по данным скорости и времени, надо скорость умножить на время.
расстояние = скорость · время
Задача. Грузовик ехал 12 часов со скоростью 70 км/ч. Какое расстояние проехал грузовик за это время?
Ответ: Грузовик за 12 часов проехал 840 км.
Задачи на движение в одном направлении
Рассмотрим задачи, в которых речь идёт о движении в одном направлении. В таких задачах два каких-нибудь объекта движутся в одном направлении с разной скоростью, отдаляясь друг от друга или сближаясь друг с другом.
Задачи на скорость сближения
Скорость сближения — это скорость, с которой объекты сближаются друг с другом.
Чтобы найти скорость сближения двух объектов, которые движутся в одном направлении, надо из большей скорости вычесть меньшую.
Задача 1. Из города выехал автомобиль со скоростью 40 км/ч. Через 4 часа вслед за ним выехал второй автомобиль со скоростью 60 км/ч. Через сколько часов второй автомобиль догонит первый?
Решение: Так как на момент выезда второго автомобиля из города первый уже был в пути 4 часа, то за это время он успел удалиться от города на:
Второй автомобиль движется быстрее первого, значит каждый час расстояние между автомобилями будет сокращаться на разность их скоростей:
Разделив расстояние между автомобилями на скорость их сближения, можно узнать, через сколько часов они встретятся:
Решение задачи по действиям можно записать так:
1) 40 · 4 = 160 (км) — расстояние между автомобилями,
Ответ: Второй автомобиль догонит первый через 8 часов.
Задача 2. Из двух посёлков между которыми 5 км, одновременно в одном направлении вышли два пешехода. Скорость пешехода, идущего впереди, 4 км/ч, а скорость пешехода, идущего позади 5 км/ч. Через сколько часов после выхода второй пешеход догонит первого?
Решение: Так как второй пешеход движется быстрее первого, то каждый час расстояние между ними будет сокращаться. Значит можно определить скорость сближения пешеходов:
Оба пешехода вышли одновременно, значит расстояние между ними равно расстоянию между посёлками (5 км). Разделив расстояние между пешеходами на скорость их сближения, узнаем через сколько второй пешеход догонит первого:
Решение задачи по действиям можно записать так:
Ответ: Через 5 часов второй пешеход догонит первого.
Задача на скорость удаления
Скорость удаления — это скорость, с которой объекты отдаляются друг от друга.
Чтобы найти скорость удаления двух объектов, которые движутся в одном направлении, надо из большей скорости вычесть меньшую.
Задача. Два автомобиля выехали одновременно из одного и того же пункта в одном направлении. Скорость первого автомобиля 80 км/ч, а скорость второго — 40 км/ч.
1) Чему равна скорость удаления между автомобилями?
2) Какое расстояние будет между автомобилями через 3 часа?
3) Через сколько часов расстояние между ними будет 200 км?
Решение: Сначала узнаем скорость удаления автомобилей друг от друга, для этого вычтем из большей скорости меньшую:
Каждый час автомобили отдаляются друг от друга на 40 км. Теперь можно узнать сколько километров будет между ними через 3 часа, для этого скорость удаления умножим на 3:
Чтобы узнать через сколько часов расстояние между автомобилями станет 200 км, надо расстояние разделить на скорость удаления:
1) Скорость удаления между автомобилями равна 40 км/ч.
2) Через 3 часа между автомобилями будет 120 км.
3) Через 5 часов между автомобилями будет расстояние в 200 км.
Текстовые задачи на движение – легко! Алгоритм решения и успех на ЕГЭ
Почему текстовые задачи относятся к простым?
Во-первых, все такие задачи решаются по единому алгоритму, о котором мы вам расскажем. Во-вторых, многие из них однотипны — это задачи на движение или на работу. Главное — знать к ним подход.
Внимание! Чтобы научиться решать текстовые задачи, вам понадобится всего три-четыре часа самостоятельной работы, то есть два-три занятия. Всё, что нужно, — это здравый смысл плюс умение решать квадратное уравнение. И даже формулу для дискриминанта мы вам напомним, если вдруг забыли.
Прежде чем перейти к самим задачам — проверьте себя.
Запишите в виде математического выражения:
Пока не напишете — в ответы не подглядывайте! 🙂
Итак, правильные ответы:
Начнем мы с задач на движение. Они часто встречаются в вариантах ЕГЭ. Здесь всего два правила:
Для начала очень внимательно читаем условие. В нем все уже есть. Помним, что текстовые задачи на самом деле очень просты.
Нарисуем таблицу. В нее сразу можно внести расстояние — и велосипедист, и автомобилист проехали по км. Можно внести скорость — она равна и для велосипедиста и автомобилиста соответственно. Осталось заполнить графу «время».
| велосипедист |
| автомобилист |
Приведем дроби в левой части к одному знаменателю.
Если вы не знаете, как приводить дроби к общему знаменателю (или — как раскрывать скобки, как решать уравнение. ), подойдите с этим конкретным вопросом к вашему учителю математики и попросите объяснить. Бесполезно говорить учительнице: «Я не понимаю математику» — это слишком абстрактно и не располагает к ответу. Учительница может ответить, например, что она вам сочувствует. Или, наоборот, даст какую-либо характеристику вашей личности. И то и другое неконструктивно.
А вот если вы зададите конкретный вопрос: «Как приводить дроби к одному знаменателю» или «Как раскрывать скобки» — вы получите нужный вам конкретный ответ. Вам ведь необходимо в этом разобраться! Если педагог занят, договоритесь о времени, когда вы можете с ним (или с ней) встретиться, чтобы получить консультацию. Используйте ресурсы, которые у вас под рукой!
Раскроем скобки и перенесем всё в левую часть уравнения:
Найдем дискриминант и корни:
Ясно, что не подходит по смыслу задачи — скорость велосипедиста не должна быть отрицательной.
Следующая задача — тоже про велосипедиста.
Как и в предыдущей задаче, сгруппируем слагаемые:
Точно так же приводим дроби к одному знаменателю:
Напомним — если вам непонятны какие-либо действия при решении уравнений, обращайтесь к учительнице! Показывайте конкретную строчку в решении задачи и говорите: «Пожалуйста, объясните, как это делать». Для нее такое объяснение — дело пятнадцати минут, а вы наконец научитесь решать уравнения, что очень важно для сдачи ЕГЭ по математике.
Найдем корни уравнения:
. Это вполне правдоподобная скорость велосипедиста. А ответ не подходит, так как скорость велосипедиста должна быть положительна.
Ты нашел то, что искал? Поделись с друзьями!
Следующий тип задач — когда что-нибудь плавает по речке, в которой есть течение. Например, теплоход, катер или моторная лодка. Обычно в условии говорится о собственной скорости плавучей посудины и скорости течения. Собственной скоростью называется скорость в неподвижной воде.
При движении по течению эти скорости складываются. Течение помогает, по течению плыть — быстрее.
Скорость при движении по течению равна сумме собственной скорости судна и скорости течения.
А если двигаться против течения? Течение будет мешать, относить назад. Теперь скорость течения будет вычитаться из собственной скорости судна.
Расстояние и в ту, и в другую сторону одинаково и равно км.
Занесем скорость и расстояние в таблицу.
| по течению |
| против течения |
Условие « на два часа больше, чем » можно записать в виде:
Приводим дроби в левой части к одному знаменателю
Умножаем обе части уравнения на
Вообще-то это уравнение имеет два корня: и (оба этих числа при возведении в квадрат дают ). Но конечно же, отрицательный ответ не подходит — скорость лодки должна быть положительной.
Теперь графа «время».
| по течению |
| против течения |
В пункт отправления теплоход вернулся через часов после отплытия из него. Стоянка длилась часов, следовательно, часов теплоход плыл — сначала по течению, затем против.
Наверное, вы уже заметили, насколько похожи все эти задачи. Текстовые задачи хороши еще и тем, что ответ легко проверить с точки зрения здравого смысла. Ясно, что если вы получили скорость течения, равную километров в час — задача решена неверно.
| по течению |
| против течения |
Приведем дроби в левой части к общему знаменателю, раскроем скобки и упростим уравнение. Получим:
Еще один тип текстовых задач в вариантах ЕГЭ по математике — это задачи на работу.
Задачи на движение (нахождение скорости) с ответами
«Управление общеобразовательной организацией:
новые тенденции и современные технологии»
Свидетельство и скидка на обучение каждому участнику
Задача 1.
Из поселка и города навстречу друг другу, одновременно выехали два автобуса. Один автобус до встречи проехал 100 км со скоростью 25 км/час. Сколько километров до встречи проехал второй автобус, если его скорость 50 км/час.
· 1) 100 : 25 = 4 (часа ехал один автобус)
· Выражение: 50 * (100 : 25) = 200
· Ответ: второй автобус проехал до встречи 200 км.
Задача 2.
Расстояние между двумя пристанями 90 км. От каждой из них одновременно навстречу друг другу вышли два теплохода. Сколько часов им понадобится чтобы встретиться, если скорость первого 20 км/час, а второго 25 км/час?
· 1) 25 + 20 = 45 (сумма скоростей теплоходов)
· Выражение: 90 : (20 + 25) = 2
· Ответ: теплоходы встретятся через 2 часа.
Задача 3.
От двух станций, расстояние между которыми 564 км., одновременно навстречу друг другу вышли два поезда. Скорость одного из них 63 км/час. Какова скорость второго, если поезда встретились через 4 часа?
· 1) 63 * 4 = 252 (прошел 1 поезд)
· Ответ: скорость второго поезда 78 км/час.
Задача 4.
Через сколько секунд встретятся две ласточки, летящие на встречу друг другу, если скорость каждой из них 23 метра в секунду, а расстояние между ними 920 м.
· 1) 23 * 2 = 46 (сумма скоростей ласточек)
· Выражение: 920 : (23 * 2) = 20
· Ответ: ласточки встретятся через 20 секунд.
Задача 5
С двух поселков, навстречу друг другу выехали одновременно велосипедист и мотоциклист. Скорость мотоциклиста 54 км/час, велосипедиста 16 км/час. Сколько километров проехал мотоциклист до встречи, если велосипедист проехал 48 км?
· 1) 48 : 16 = 3 (часа потратил велосипедист)
· Выражение: 54 * (48 : 16) = 162
· Ответ: мотоциклист проехал 162 км.
Задача 6
Две лодки, расстояние между которыми 90 км, начали движение на встречу друг другу. Скорость одной из лодок 10 км /час, другой 8 км/час. Сколько часов понадобится лодкам, чтобы встретится?
· 1) 10 + 8 = 18 (скорость двух лодок вместе)
· Выражение: 90 : (10 + 8) = 5
· Ответ: лодки встретятся через 5 часов.
Задача 7
По дорожке, длинна которой 200 метров, навстречу друг другу побежали два мальчика. Один из них бежал со скоростью 5 м/сек. Какова скорость второго мальчика, если встретились они через 20 сек?
· 1) 20 * 5 = 100 (метров пробежал первый мальчик)
· Ответ: скорость второго мальчика 5 км/сек.
Задача 8
Два поезда выехали навстречу друг другу. Скорость одного из них 35 км/час, другого 29 км/час. Какое расстояние между поездами было сначала, если встретились они через 5 часов?
· 1) 35 + 29 = 64 (скорсть двух поездов вместе)
· Выражение: (35 + 29) * 5 = 320
· Ответ: расстояние между поездами было 320 км.
Задача 9
Из двух поселков навстречу друг другу выехали два всадника. Скорость одного из них 13 км/час, встретились они через 4 часа. С какой скоростью двигался второй всадник, если расстояние между поселками 100 км.
· 1) 13 * 4 = 52 (проехал первый всадник)
· Ответ: скорость второго всадника 12 км/час.
Задача 1
Грузовой поезд проехал 420 км, сделав остановку на одной станции. Путь до этой станции занял 4 часа при скорости 80км/час. Весь оставшийся путь занял 2 часа. С какой скоростью поезд двигался после остановки?
· Ответ: Поезд после остановки двигался со скоростью 50 км/час
Задача 2
Грузовик в первый день проехал 600 км, а во второй день 200 км. Весь путь занял 8 часов. Сколько часов в день проезжал грузовик, если он ехал все время с одинаковой скоростью.
· Ответ: в первый день 6 часов, во второй 2 часа.
Задача 3
Велосипедист проезжает путь из города в поселок, со скоростью 17 км/час, за 5 часов. Сколько времени потребуется пешеходу, что бы пройти этот же путь, если он движется со скоростью 5 км/час?
· Ответ: пешеходу понадобится 17 часов.
Задача 4
Автомобиль проехал 400 километров. Двигаясь со скоростью 60 км/час, он проехал за 2 часа первую часть пути. С какой скоростью он двигался остальную часть пути, если он затратил на нее 4 часа?
Задача 5
Скворец летел со скоростью 75 км/час 2 часа. С какой скоростью летит ворона, если такое же расстояние она пролетит за 3 часа?
· Ответ: скорость вороны 50 км/час.
Задача 6
Автотуристы были в пути 15 часов в течение 2 дней. 420 километров они проехали в первый день и 480 во второй. Сколько часов каждый день они были в пути, если каждый день они двигались с одинаковой скоростью?
· Ответ: в первый день 7 часов, во второй 8.
Задача 7
От города до поселка 37 километров, а от этого поселка до следующего 83 км. Сколько времени понадобиться, что бы доехать от города до последнего поселка, если двигаться со скоростью 40 км/час?
Задача 8
За 3 часа катер преодолел расстояние в 210 км. Какое расстояние оно пройдет за 5 часов, если его скорость увеличится на 5 км/час?
Задача 9
Теплоход за 9 часов прошел 360 км в первый день. Во второй день теплоход с прежней скоростью был в пути 12 часов. Сколько всего километров преодолел теплоход за 2 дня?
Задача 10
Вертолет пролетает за 4 часа 960 километров. Сколько времени понадобится самолету, чтобы пролететь то же расстояние, если он движется в 2 раз быстрее?
Задача 1.
Машина и автобус выехали с автостанции одновременно в противоположных направлениях. Скорость автобуса в два раза меньше скорости автомобиля. Через сколько часов расстояние между ними будет 450 км, если скорость автомобиля 60 км/час?
· 1) 60 : 2 = 30 (скорость автобуса)
· 2) 60 + 30 = 90 (скорость автобуса и автомобиля вместе)
· Выражение: 450 : (60 : 2 + 60) = 5
· Ответ: через 5 часов.
Задача 2.
Из города на дачу выехал велосипедист со скоростью 12 км/час. Дорога на дачу заняла 6 часов. На сколько изменилась скорость велосипедиста на обратном пути, если он затратил на него 4 часа?
· 1) 12 * 6 = 72 (расстояние от города к даче)
· 2) 72 : 4 = 18 (скорость обратного пути велосипедиста)
· Ответ: скорость велосипедиста увеличилась на 6 км/час.
Задача 3.
Два поезда одновременно начали движение в противоположных на правлениях. Один двигался со скоростью на 30 км/час меньше, чем другой. На каком расстоянии друг от друга поезда будут через 4 часа, если скорость другого поезда 130 км/час?
· 2) 130 + 100 = 230 (скорость двух поездов вместе)
· Ответ: расстояние между поездами через 4 часа будет 920 км.
Задача 4.
Такси двигалось со скоростью 60 км/час, автобус в 2 раза медленнее. Через сколько времени между ними будет 360 км, если они движутся в разных направлениях?
· 1) 60 : 2 = 30 (скорость автобуса)
· 2) 60 + 30 = 90 (скорость автобуса и такси вместе)
· Выражение: 360 : (60 : 2 + 60) = 4
· Ответ: через 4 часа.
Задача 5.
Два автомобиля выехали из автопарка одновременно в противоположных направлениях. Скорость одного 70 км/час, другого 50 км/час. Какое расстояние будет между ними через 4 часа?
· 1) 70 + 50 = 120 (скорость двух автомобилей вместе)
· Выражение: (70 + 50) : 4 = 480
· Ответ: через 4 часа между автомобилями будет 480 км.
Задача 6.
Два человека в одно и тоже время вышли из поселка в разных направлениях. Один двигался со скоростью 6 км/час, скорость другого была 5 км/час. Сколько часов понадобится чтобы расстояние между ними стало 33 км?
· 1) 6 + 5 = 11 (скорость двух человек вместе)
· Выражение: 33 : ( 6 + 5) = 3
· Ответ: через 3 часа.
Задача 7.
Грузовой и легковой автомобили отправились от автостанции в разных направлениях. За одно и тоже время грузовик проехал 70 км, а легковой автомобиль 140 км. С какой скоростью двигался легковой автомобиль, если скорость грузовика 35 км/час?
· 1) 70 : 35 = 2 (часа затратил на дорогу грузовик)
· Выражение: 140 : (70 : 35) = 70
· Ответ: скорость легкового автомобиля 70 км/час.
Задача 8.
Два пешехода вышли из турбазы в противоположных направлениях. Скорость одного из них 4 км/час, другого 5 км/час. Какое расстояние будет между пешеходами через 5 часов?
· 1) 4 + 5 = 11 (общая скорсть пешеходов)
· Выражение: (4 + 5) * 5 = 55
· Ответ: через 5 часов между пешеходами будет 55 км.
Задача 9.
Два самолета одновременно вылетели в противоположных направлениях. Скорость одного из самолетов 640 км/час. Какая скорость другого самолета, если через 3 часа расстояние между ними было 3630 км?
· 1) 640 * 3 = 1920 (км пролетел один самолет)
· Ответ: скорсть второго самолета 570 км/ч
Задача 10.
Два крестьянина вышли из одного поселка одновременно в противоположных направлениях. Один двигался со скоростью 3 км/час другой 6 км/час. Какое расстояние будет между крестьянами через 5 часов.
· 1) 3 + 6 = 9 (скорость двух крестьян вместе)
· Выражение: 5 * (3 + 6) = 45
· Ответ: через 5 часов между крестьянами будет 45 км.
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Скоростное чтение
Курс повышения квалификации
Актуальные вопросы теории и методики преподавания в начальной школе в соответствии с ФГОС НОО
Ищем педагогов в команду «Инфоурок»
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
также Вы можете выбрать тип материала:
Общая информация
Похожие материалы
Сценарий праздника ко дню матери
Разработка урока русского языка «Сложные слова» (3 класс)
Сценарий игры-путешествия по станциям 1-4 классы
Урок литературы в 4 классе И.Тургенев «Перепёлка»
Конспект урока математики 4 класс «Распределительные свойства умножения относительно сложения и умножения «
Презентация к уроку окружающего мира на тему «Духовный мир древнего человека. Язычество.»
Не нашли то что искали?
Воспользуйтесь поиском по нашей базе из
5437601 материал.
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Во всех педвузах страны появятся технопарки
Время чтения: 1 минута
В Минпросвещения рассказали о формате обучения школьников после праздников
Время чтения: 1 минута
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
ОНФ планирует решить проблему с низкими зарплатами водителей школьных автобусов в России
Время чтения: 1 минута
Итоговое сочинение успешно написали более 97% выпускников школ
Время чтения: 2 минуты
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.