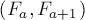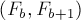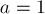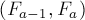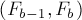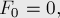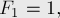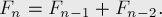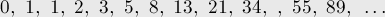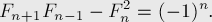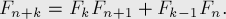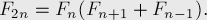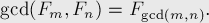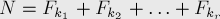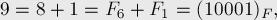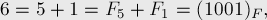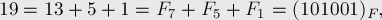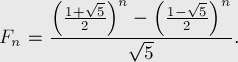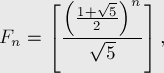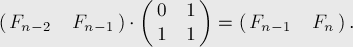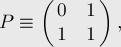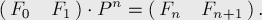как определить номер числа фибоначчи

Находим N’е число Фибоначчи тремя способами за приемлемое время: основы динамического программирования

Задача: посчитать N-е число последовательности, в которой каждый элемент равен сумме двух предыдущих. Такая последовательность называется последовательностью Фибоначчи: 1, 1, 2, 3, 5, 8…

Очень часто на разнообразных олимпиадах попадаются задачи вроде этой, которые, как думается на первый взгляд, можно решить с помощью простого перебора. Но если мы подсчитаем количество возможных вариантов, то сразу убедимся в неэффективности такого подхода: например, простая рекурсивная функция, приведенная ниже, будет потреблять существенные ресурсы уже на 30-ом числе Фибоначчи, тогда как на олимпиадах время решения часто ограничено 1-5 секундами.

Давайте подумаем, почему так происходит. Например, для вычисления fibo(30) мы сначала вычисляем fibo(29) и fibo(28). Но при этом наша программа «забывает», что fibo(28) мы уже вычисляли при поиске fibo(29).

Основная ошибка такого подхода «в лоб» в том, что одинаковые значения аргументов функции исчисляются многократно — а ведь это достаточно ресурсоемкие операции. Избавиться от повторяющихся вычислений нам поможет метод динамического программирования — это прием, при использовании которого задача разбивается на общие и повторяющиеся подзадачи, каждая из которых решается только 1 раз — это значительно повышает эффективность программы. Этот метод подробно описан в нашей статье, там же есть и примеры решения других задач.

Самый просто вариант улучшения нашей функции — запоминать, какие значения мы уже вычисляли. Для этого нужно ввести дополнительный массив, который будет служить как бы «кэшем» для наших вычислений: перед вычислением нового значения мы будем проверять, не вычисляли ли его раньше. Если вычисляли, то будем брать из массива готовое значение, а если не вычисляли — придётся считать его на основе предыдущих и запоминать на будущее:

Так как в данной задаче для вычисления N-ого значения нам гарантированно понадобится (N-1)-е, то не составит труда переписать формулу в итерационный вид — просто будем заполнять наш массив подряд до тех пор, пока не дойдём до нужной ячейки:

Теперь мы можем заметить, что когда мы вычисляем значение F(N), то значение F(N-3) нам уже гарантированно никогда не понадобится. То есть нам достаточно хранить в памяти лишь два значения — F(N-1) и F(N-2). Причём, как только мы вычислили F(N), хранение F(N-2) теряет всякий смысл. Попробуем записать эти размышления в виде кода:

Бывалому программисту понятно, что код выше, в общем-то ерунда, так как cache3 никогда не используется (он сразу записывается в cache2 ), и всю итерацию можно переписать, используя всего одно выражение:

Для тех, кто не может понять, как работает магия с остатком от деления, или просто хочет увидеть более неочевидную формулу, существует ещё одно решение:

Попробуйте проследить за выполнением этой программы: вы убедитесь в правильности алгоритма.

P.S. Вообще, существует единая формула для вычисления любого числа Фибоначчи, которая не требует никаких итераций или рекурсии:

Но, как можете догадаться, подвох в том, что цена вычисления степеней нецелых чисел довольно велика, как и их погрешность.

Хинт для программистов: если зарегистрируетесь на соревнования Huawei Cup, то бесплатно получите доступ к онлайн-школе для участников. Можно прокачаться по разным навыкам и выиграть призы в самом соревновании.

Перейти к регистрации

Источник

Числа Фибоначчи.Определение порядкового номера элемента

Определение порядкового номера наименьшей цифры числа
Написать программу, определяющую порядковый номер цифры. На вход подается большое число, на выходе.

Вывод порядкового номера элемента последовательности
Дано целое n>0 и последовательность из n вещественных чисел, среди которых есть хотя бы одно.

Набрать с чисел Фибоначчи в интервале от 1 до 100, только просто числа, а также их порядковые номера в ряду Фибоначчи
Помогите с задачкой Набрать с чисел Фибоначчи в интервале от 1 до 100, только просто числа, а.

Вывести на экран все числа, номера которых есть числа Фибоначчи
Вывести на экран все числа заданной последовательности, номера которых есть числа Фибоначчи.

Помощь в написании контрольных, курсовых и дипломных работ здесь.

Определение номера первого максимального элемента в однородном массиве
написать функцию для определения номера первого максимального элемента в однородном массиве.

Определение номера треугольного числа
Напишите на языке C / C++ программу, определяющую номер треугольного числа. Вход: одно целое.

Поиск минимального значения элемента и определение порядкового номера наименьшего элемента
Необходимо написать программу, формирующую рандомный одномерный массив, а после определяющую.

Источник

5 способов вычисления чисел Фибоначчи: реализация и сравнение

Введение

Программистам числа Фибоначчи должны уже поднадоесть. Примеры их вычисления используются везде. Всё от того, что эти числа предоставляют простейший пример рекурсии. А ещё они являются хорошим примером динамического программирования. Но надо ли вычислять их так в реальном проекте? Не надо. Ни рекурсия, ни динамическое программирование не являются идеальными вариантами. И не замкнутая формула, использующая числа с плавающей запятой. Сейчас я расскажу, как правильно. Но сначала пройдёмся по всем известным вариантам решения.

Код предназначен для Python 3, хотя должен идти и на Python 2.

Для начала – напомню определение:

Замкнутая формула

Решаем квадратное уравнение:

Откуда и растёт «золотое сечение» ϕ=(1+√5)/2. Подставив исходные значения и проделав ещё вычисления, мы получаем:

что и используем для вычисления F_n.

Хорошее:
Быстро и просто для малых n
Плохое:
Требуются операции с плавающей запятой. Для больших n потребуется большая точность.
Злое:
Использование комплексных чисел для вычисления F_n красиво с математической точки зрения, но уродливо — с компьютерной.

Рекурсия

Самое очевидное решение, которое вы уже много раз видели – скорее всего, в качестве примера того, что такое рекурсия. Повторю его ещё раз, для полноты. В Python её можно записать в одну строку:

Хорошее:
Очень простая реализация, повторяющая математическое определение
Плохое:
Экспоненциальное время выполнения. Для больших n очень медленно
Злое:
Переполнение стека

Запоминание

У решения с рекурсией есть большая проблема: пересекающиеся вычисления. Когда вызывается fib(n), то подсчитываются fib(n-1) и fib(n-2). Но когда считается fib(n-1), она снова независимо подсчитает fib(n-2) – то есть, fib(n-2) подсчитается дважды. Если продолжить рассуждения, будет видно, что fib(n-3) будет подсчитана трижды, и т.д. Слишком много пересечений.

Поэтому надо просто запоминать результаты, чтобы не подсчитывать их снова. Время и память у этого решения расходуются линейным образом. В решении я использую словарь, но можно было бы использовать и простой массив.

(В Python это можно также сделать при помощи декоратора, functools.lru_cache.)

Хорошее:
Просто превратить рекурсию в решение с запоминанием. Превращает экспоненциальное время выполнение в линейное, для чего тратит больше памяти.
Плохое:
Тратит много памяти
Злое:
Возможно переполнение стека, как и у рекурсии

Динамическое программирование

После решения с запоминанием становится понятно, что нам нужны не все предыдущие результаты, а только два последних. Кроме этого, вместо того, чтобы начинать с fib(n) и идти назад, можно начать с fib(0) и идти вперёд. У следующего кода линейное время выполнение, а использование памяти – фиксированное. На практике скорость решения будет ещё выше, поскольку тут отсутствуют рекурсивные вызовы функций и связанная с этим работа. И код выглядит проще.

Это решение часто приводится в качестве примера динамического программирования.

Хорошее:
Быстро работает для малых n, простой код
Плохое:
Всё ещё линейное время выполнения
Злое:
Да особо ничего.

Матричная алгебра

И, наконец, наименее освещаемое, но наиболее правильное решение, грамотно использующее как время, так и память. Его также можно расширить на любую гомогенную линейную последовательность. Идея в использовании матриц. Достаточно просто видеть, что

А обобщение этого говорит о том, что

Два значения для x, полученных нами ранее, из которых одно представляло собою золотое сечение, являются собственными значениями матрицы. Поэтому, ещё одним способом вывода замкнутой формулы является использование матричного уравнения и линейной алгебры.

Так чем же полезна такая формулировка? Тем, что возведение в степень можно произвести за логарифмическое время. Это делается через возведения в квадрат. Суть в том, что

где первое выражение используется для чётных A, второе для нечётных. Осталось только организовать перемножения матриц, и всё готово. Получается следующий код. Я организовал рекурсивную реализацию pow, поскольку её проще понять. Итеративную версию смотрите тут.

Хорошее:
Фиксированный объём памяти, логарифмическое время
Плохое:
Код посложнее
Злое:
Приходится работать с матрицами, хотя они не так уж и плохи

Сравнение быстродействия

Сравнивать стоит только вариант динамического программирования и матрицы. Если сравнивать их по количеству знаков в числе n, то получится, что матричное решение линейно, а решение с динамическим программированием – экспоненциально. Практический пример – вычисление fib(10 ** 6), числа, у которого будет больше двухсот тысяч знаков.

n = 10 ** 6
Вычисляем fib_matrix: у fib(n) всего 208988 цифр, расчёт занял 0.24993 секунд.
Вычисляем fib_dynamic: у fib(n) всего 208988 цифр, расчёт занял 11.83377 секунд.

Теоретические замечания

Не напрямую касаясь приведённого выше кода, данное замечание всё-таки имеет определённый интерес. Рассмотрим следующий граф:

Подсчитаем количество путей длины n от A до B. Например, для n = 1 у нас есть один путь, 1. Для n = 2 у нас опять есть один путь, 01. Для n = 3 у нас есть два пути, 001 и 101. Довольно просто можно показать, что количество путей длины n от А до В равно в точности F_n. Записав матрицу смежности для графа, мы получим такую же матрицу, которая была описана выше. Это известный результат из теории графов, что при заданной матрице смежности А, вхождения в А n — это количество путей длины n в графе (одна из задач, упоминавшихся в фильме «Умница Уилл Хантинг»).

Почему на рёбрах стоят такие обозначения? Оказывается, что при рассмотрении бесконечной последовательности символов на бесконечной в обе стороны последовательности путей на графе, вы получите нечто под названием «подсдвиги конечного типа», представляющее собой тип системы символической динамики. Конкретно этот подсдвиг конечного типа известен, как «сдвиг золотого сечения», и задаётся набором «запрещённых слов» <11>. Иными словами, мы получим бесконечные в обе стороны двоичные последовательности и никакие пары из них не будут смежными. Топологическая энтропия этой динамической системы равна золотому сечению ϕ. Интересно, как это число периодически появляется в разных областях математики.

Источник

Определить номер числа Фибоначчи значение которого равно заданному числу

Вотм мой код, но он не верный.

Определить номер элемента массива значение которого равно заданному числу
Дано вещественное число А и массив Х(10). Определить номер элемента, равного числу А. Если такого.

Определить номер последнего элемента, значение которого равно 7.
Определить номер последнего элемента, значение которого равно 7.

Определить первый номер элемента массива С[1..8], значение которого равно Р
Определить первый номер элемента массива С, значение которого равно Р

Решение

Black Fregat, плавающая точка в целочисленной задаче.

Добавлено через 15 минут

Помощь в написании контрольных, курсовых и дипломных работ здесь.

Найти номер первого числа Фибоначчи, значение которого превышает 100
Найти номер первого числа Фибоначчи, значение которого превышает 100. Очень буду благодарна.

Присвоить переменной К номер элемента массива, равно заданному числу.
Задан массив целых чисел X, упорядоченный по возрастанию, а также целое число Y. Присвоить.

Определить номер элемента массива A$, значение которого равно значению заданной символьной переменной C$
Определить номер элемента массива A$, значение которого равно значению заданной символьной.

Определить номер элемента списка, значение которого равно сумме первого и последнего элементов
Как реализовать данную задачу на Prolog? Определять номер элемента списка из целых чисел, значение.

Источник

Числа Фибоначчи

Определение

Последовательность Фибоначчи определяется следующим образом:

Несколько первых её членов:

История

Эти числа ввёл в 1202 г. Леонардо Фибоначчи (Leonardo Fibonacci) (также известный как Леонардо Пизанский (Leonardo Pisano)). Однако именно благодаря математику 19 века Люка (Lucas) название «числа Фибоначчи» стало общеупотребительным.

Впрочем, индийские математики упоминали числа этой последовательности ещё раньше: Гопала (Gopala) до 1135 г., Хемачандра (Hemachandra) — в 1150 г.

Числа Фибоначчи в природе

Сам Фибоначчи упоминал эти числа в связи с такой задачей: «Человек посадил пару кроликов в загон, окруженный со всех сторон стеной. Сколько пар кроликов за год может произвести на свет эта пара, если известно, что каждый месяц, начиная со второго, каждая пара кроликов производит на свет одну пару?». Решением этой задачи и будут числа последовательности, называемой теперь в его честь. Впрочем, описанная Фибоначчи ситуация — больше игра разума, чем реальная природа.

Индийские математики Гопала и Хемачандра упоминали числа этой последовательности в связи с количеством ритмических рисунков, образующихся в результате чередования долгих и кратких слогов в стихах или сильных и слабых долей в музыке. Число таких рисунков, имеющих в целом долей, равно .

Числа Фибоначчи появляются и в работе Кеплера 1611 года, который размышлял о числах, встречающихся в природе (работа «О шестиугольных снежинках»).

Интересен пример растения — тысячелистника, у которого число стеблей (а значит и цветков) всегда есть число Фибоначчи. Причина этого проста: будучи изначально с единственным стеблем, этот стебель затем делится на два, затем от главного стебля ответвляется ещё один, затем первые два стебля снова разветвляются, затем все стебли, кроме двух последних, разветвляются, и так далее. Таким образом, каждый стебель после своего появления «пропускает» одно разветвление, а затем начинает делиться на каждом уровне разветвлений, что и даёт в результате числа Фибоначчи.

Вообще говоря, у многих цветов (например, лилий) число лепестков является тем или иным числом Фибоначчи.

Также в ботанике известно явление »филлотаксиса». В качестве примера можно привести расположение семечек подсолнуха: если посмотреть сверху на их расположение, то можно увидеть одновременно две серии спиралей (как бы наложенных друг на друга): одни закручены по часовой стрелке, другие — против. Оказывается, что число этих спиралей примерно совпадает с двумя последовательными числами Фибоначчи: 34 и 55 или 89 и 144. Аналогичные факты верны и для некоторых других цветов, а также для сосновых шишек, брокколи, ананасов, и т.д.

Для многих растений (по некоторым данным, для 90% из них) верен и такой интересный факт. Рассмотрим какой-нибудь лист, и будем спускаться от него вниз до тех пор, пока не достигнем листа, расположенного на стебле точно так же (т.е. направленного точно в ту же сторону). Попутно будем считать все листья, попадавшиеся нам (т.е. расположенные по высоте между стартовым листом и конечным), но расположенными по-другому. Нумеруя их, мы будем постепенно совершать витки вокруг стебля (поскольку листья расположены на стебле по спирали). В зависимости от того, совершать витки по часовой стрелке или против, будет получаться разное число витков. Но оказывается, что число витков, совершённых нами по часовой стрелке, число витков, совершённых против часовой стрелки, и число встреченных листьев образуют 3 последовательных числа Фибоначчи.

Впрочем, следует отметить, что есть и растения, для которых приведённые выше подсчёты дадут числа из совсем других последовательностей, поэтому нельзя сказать, что явление филлотаксиса является законом, — это скорее занимательная тенденция.

Свойства

Числа Фибоначчи обладают множеством интересных математических свойств.

Вот лишь некоторые из них:

всегда кратно .

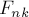
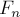
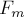
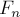
если кратно , то кратно .

Фибоначчиева система счисления

Теорема Цекендорфа утверждает, что любое натуральное число можно представить единственным образом в виде суммы чисел Фибоначчи:

где , , , (т.е. в записи нельзя использовать два соседних числа Фибоначчи).

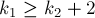
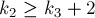
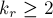
Отсюда следует, что любое число можно однозначно записать в фибоначчиевой системе счисления, например:

причём ни в каком числе не могут идти две единицы подряд.

Нетрудно получить и правило прибавления единицы к числу в фибоначчиевой системе счисления: если младшая цифра равна 0, то её заменяем на 1, а если равна 1 (т.е. в конце стоит 01), то 01 заменяем на 10. Затем «исправляем» запись, последовательно исправляя везде 011 на 100. В результате за линейное время будет получена запись нового числа.

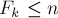
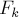
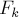
Перевод числа в фибоначчиеву систему счисления осуществляется простым «жадным» алгоритмом: просто перебираем числа Фибоначчи от больших к меньшим и, если некоторое , то входит в запись числа , и мы отнимаем от и продолжаем поиск.

Формула для n-го числа Фибоначчи

Формула через радикалы

Существует замечательная формула, называемая по имени французского математика Бине (Binet), хотя она была известна до него Муавру (Moivre):

Эту формулу легко доказать по индукции, однако вывести её можно с помощью понятия образующих функций или с помощью решения функционального уравнения.

Сразу можно заметить, что второе слагаемое всегда по модулю меньше 1, и более того, очень быстро убывает (экспоненциально). Отсюда следует, что значение первого слагаемого даёт «почти» значение 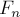. Это можно записать в строгом виде:

где квадратные скобки обозначают округление до ближайшего целого.

Впрочем, для практического применения в вычислениях эти формулы мало подходят, потому что требуют очень высокой точности работы с дробными числами.

Матричная формула для чисел Фибоначчи

Нетрудно доказать матричное следующее равенство:

Но тогда, обозначая

Таким образом, для нахождения -го числа Фибоначчи надо возвести матрицу в степень .

Вспоминая, что возведение матрицы в -ую степень можно осуществить за (см. Бинарное возведение в степень), получается, что -ое число Фибоначчи можно легко вычислить за c использованием только целочисленной арифметики.

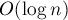
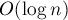
Периодичность последовательности Фибоначчи по модулю

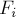
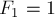
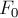
Рассмотрим последовательность Фибоначчи по некоторому модулю . Докажем, что она является периодичной, и причём период начинается с (т.е. предпериод содержит только ).

Докажем это от противного. Рассмотрим 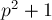пар чисел Фибоначчи, взятых по модулю :

Поскольку по модулю может быть только различных пар, то среди этой последовательности найдётся как минимум две одинаковые пары. Это уже означает, что последовательность периодична.

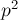
Выберем теперь среди всех таких одинаковых пар две одинаковые пары с наименьшими номерами. Пусть это пары с некоторыми номерами и . Докажем, что . Действительно, в противном случае для них найдутся предыдущие пары и , которые, по свойству чисел Фибоначчи, также будут равны друг другу. Однако это противоречит тому, что мы выбрали совпадающие пары с наименьшими номерами, что и требовалось доказать.

Источник